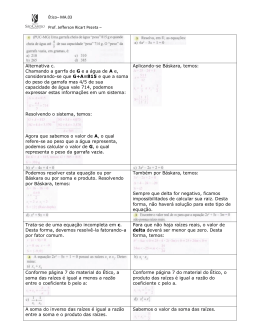
Função polinomial do 2º grau –Pág. 132
Prof. Jefferson Ricart Pezeta
Para resolver cada item, basta calcular as
raízes das equações de 2º grau.
Para fazer o esboço de cada gráfico, devemos
primeiro calcular as raízes das equações. Uma
vez determinadas as raízes, devemos verificar
se a concavidade aponta para baixo (a<0) ou
para cima (a>0). Feito isso, basta fazer o
esboço conforme resoluções abaixo.
Para cada item solicitado deveremos ter
como referência o valor de delta. Para dois
zeros diferentes o valor de delta deverá ser
maior do que zero. Para dois zeros iguais
delta será igual a zero e, para nenhum zero
real delta deverá ser menor do que zero..
Zero de uma função são os valores possíveis
que x poderá assumir para que o valor
numérico da função seja zero. O exercício
informa no em enunciado que a função admite
o 2 como um dos zeros. Desta forma, basta
substituirmos x por 2. Ao efetuarmos a
substituição proposta, teremos como única
incógnita a letra k. Isolando-se o k obteremos
seu valor.
Para resolvermos este exercício devemos
recordar de dois conceitos já aprendidos.
a) A soma de duas raízes em uma equação é
igual a c/a.
b) O produto de duas raízes em uma
equação é igual a –b/a.
A partir da duas definições acima, temos os
valores de a e b.
Para que a soma das raízes seja igual ao seu
produto, temos que:
Basta substituirmos os coeficientes a, b e c
pelos valores informados no enunciado e
isolarmos a variável k.
Substituindo a e b pelos valores calculados,
temos a função f(x)=-x2+3x+10
Analisando a concavidade e as raízes,
temos:
Os pontos (coordenadas) onde o gráfico
corta o eixo das abscissas (eixo x)
solicitados no enunciado são nada mais nada
menos do que os zeros da função. Já o ponto
onde o gráfico corta o eixo das ordenadas
(eixo y) é sempre o valor do coeficiente c.
Desta forma, temos:
Encontrar o eixo OX representa dizer que a
parábola passará pelo eixo x quando y for
igual a zero. Este ponto já é informado pelo
enunciado. É o ponto P. Assim sendo, para
calcularmos os valores de a e b, devemos
calcular f(x) quando f(3)=0.
Agora que temos os valores dos coeficientes a
e c devemos substituí-los na equação de 2º
grau. Desta forma, poderemos definir o valor
de b.
Observe que chegamos a uma equação de 2º
grau com a incógnita em b. Resolvendo a
equação obteremos b
Agora que temos o valor de b basta substituílo em
e obteremos o valor de a.
Ainda tem dúvidas sobre algum exercício esta página. Poste no blog ou me pergunte em sala
de aula.