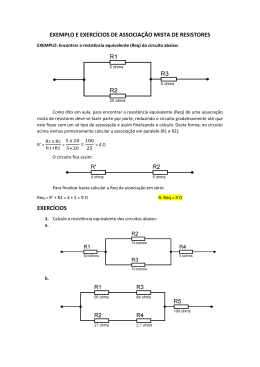
CORREÇÃO DAS ATIVIDADES DAS PÁGINAS 331, 332, 334, 335, 336, 337 e 338.
Página 331. ATIVIDADE 1
1. Sim. Basta associá-las em série com a bateria.
2. Neste circuito temos uma tensão ( U ) de 12 V e 3 resistores, cada um com um valor de resistência diferente.
R1 = 2 Ω, R2 = 3 Ω e R3 = 1 Ω.
a) A resistência equivalente (Req) em circuito com resistores em série é igual à soma de todas as suas resistências.
Neste caso: Req = R1 + R2 + R3 → Req = 2 + 3 +1 → Req = 6 Ω
b) Se temos o valor da Tensão ( U ) e o valor da resistência total (Req) do circuito podemos encontrar a intensidade
deste circuito usando a 1ª Lei de Ohm: R = U/i
U = 12 V
R = U/i
6 = 12/i
6 . i = 12
i = 12/6 i = 2 A
R=6Ω
i=?
c) Sabemos a tensão total, que é igual a 12 V e a intensidade que é de 2 A. Queremos saber agora qual a tensão
aplicada em cada um dos resistores já que possuem diferentes valores (R1 = 2 Ω, R2 = 3 Ω e R3 = 1 Ω). Usaremos a 1ª
lei de Ohm em cada resistor.
R1 = 2 Ω e a tensão ( U ) em R1 = ?
R1 = U/i 2 = U/2 U = 2 . 2 U = 4 V
R2 = 3 Ω e a tensão ( U ) em R2 = ?
R2 = U/i 3 = U/2 U = 3 . 2 U = 6 V
R3 = 1 Ω e a tensão ( U ) em R3 = ?
R3 = U/i 1 = U/2 U = 1 . 2 U = 2 V
d) Neste caso já havia sido dada a tensão total do circuito (12 V). Mas se não tivesse sido dada, bastaria somar as
tensões de cada resistor:
Tensão ( U ) em R1 = 4 V + tensão ( U ) em R2 = 6 V + tensão ( U ) em R3 = 2 V
Utotal = 12 V
Página 332. ATIVIDADE EXPERIMENTAL II
B – Sim. as duas lâmpadas apresentam o mesmo brilho.
C – Continua acesa e com o mesmo brilho.
E – Sim. As três apresentam o mesmo brilho. A tensão é a mesma em todas as lâmpadas.
F – Continuam acesas e com o mesmo brilho.
G – Só ela apaga. As outras continuam acesas e com o mesmo brilho.
H – Continuam acesas e funcionando adequadamente. É como se cada lâmpada fosse independente (estivesse
sozinha) no circuito. A ddp é mesma em cada lâmpada do circuito.
Página 334. ATIVIDADE 2
a) No circuito fechado da ilustração, os resistores estão associados em paralelo.
b) Repare que em circuitos paralelos a corrente tem mais de um caminho para percorrer e neste caso podemos dizer
que temos dois circuitos distintos e intensidades diferentes. Circuito 1, com tensão (U) de 12 V e resistência (R1) de 4
Ω e circuito 2, com tensão de 12 V e R2 de 6 Ω. Primeiro vamos achar a intensidade de cada um usando a 1 Lei de
Ohm:
i1 → R1 = U/i1 4 = 12/ i1 4 . i1 = 12 i1 = 12/4
i1 = 3 A
i2 → R2 = U/i2 6 = 12/ i2 6 . i2 = 12 i2 = 12/6
i2 = 2 A
c) Em circuitos paralelos a intensidade total é igual a soma das intensidades de corrente:
itotal = i1 + i2 itotal = 3 + 2 itotal = 5 A.
d) A resistência equivalente (Req) do circuito será:
Se temos a tensão total (12 V) e a intensidade total (5 A), usaremos a 1ª Lei de Ohm para encontrar a resistência total:
U = 12 V
R = U/i
Req = 12/5
Req = 2,4 Ω.
i=5A
Req = ?
e) Se encontramos a tensão total e a intensidade total de um circuito, podemos encontrar sua resistência total (Req)
sem precisar usar a soma dos inversos.
1/ Req = U/i 1/Req = 1/R1 + 1/R2 1/Req = 1/4 + 1/6 1/Req = (6 + 4)/24 1/Req = 10/24 Req . 10 = 24 Req = 24/10
Req = 2,4 Ω.
Página 335. ATIVIDADE EXPERIMENTAL III
1. Não. A lâmpada A tem brilho mais intenso. As lâmpadas B e C apresentam o mesmo brilho entre as duas, porém
menor do que a lâmpada A.
2. Continuam acesas e com o mesmo brilho.
3. A lâmpada B apaga, pois este ramo do circuito fica aberto. A lâmpada A continua acesa e com o mesmo brilho.
4. As lâmpadas B e C.
5. Apenas 1,5 V, pois está em série com a lâmpada B dividindo a tensão. A lâmpada B também recebe apenas 1,5 V.
6. 3 V. Ela está associada em paralelo com as outras duas lâmpadas.
7. Na lâmpada A. Ela recebe a ddp integral da fonte, 3 V, enquanto as outras duas lâmpadas dividem 3 V entre elas.
Página 337. ATIVIDADE 3
a)
L1
12 Ω
L2
12 Ω
L3
12 Ω
L4
12 Ω
b) em série.
c) em série.
d) em paralelo.
e) Achar a resistência total ou resistência equivalente (Req) do circuito. Observe que se trata de um circuito misto, com
resistores em série e em paralelo. Então resolveremos por etapas.
1º passo: Achar a Req do ramo onde estão associados em série os resistores L1 e L3; Req = 12 Ω + 12 Ω Req = 24 Ω
2º passo: Achar a Req do ramo onde estão associados em série os resistores L2 e L4; Req = 12 Ω + 12 Ω Req = 24 Ω
Obs: Lembrando que em circuito com resistores associados em série a Req = soma de seus resistores.
3º passo: determinar a resistência equivalente do circuito.
Como L1 + L3 = 24 Ω e L2 + L4 = 24 Ω e eles estão em paralelo usamos a soma dos inversos.
1/Req = 1/24 + 1/24
1/Req = 2/24 Req . 2 = 24
Req = 24/2
Req = 12 Ω
f) Calcular a intensidade de corrente na bateria.
Se fosse um circuito simples, com os resistores numa mesma série, a intensidade seria a mesma em qualquer ponto
do circuito, mas como é um circuito em série e em paralelo, cada ramo pode ter uma intensidade diferente. Então
acharemos primeiro a intensidade em cada ramo usando a 1ª Lei de Ohm.
1º passo: intensidade do ramo L1 + L3;
R = 24 Ω R = U/i
24 = 12/ i 24 . i = 12
i = 12/24
i = 0,5 A (intensidade do ramo L1 + L3)
U = 12 V
i=?
2º passo: intensidade do ramo L2 + L4;
R = 24 Ω R = U/i
24 = 12/ i 24 . i = 12
i = 12/24
i = 0,5 A (intensidade do ramo L2 + L4)
U = 12 V
i=?
Obs: Como neste circuito as resistências são iguais, as intensidades da corrente também serão iguais.
3º passo: intensidade total da corrente;
Em circuitos paralelos basta somar as intensidades de cada ramo.
intensidade do ramo L1 + L3 = 0,5 A
i = 0,5 + 0,5
i=1A
intensidade do ramo L2 + L4 = 0,5 A
Obs: Poderíamos achar também a intensidade total usando a 1ª lei de Ohm, já que temos a Req e a tensão.
Req =12 Ω
R = U/i
12 = 12/i
12 . i = 12
i = 12/12
i=1A
U = 12 V
i=?
Obs: Também podemos achar a resistência equivalente (total) deste circuito usando a 1ª Lei de Ohm. Basta encontrar
antes a intensidade total do circuito, evitando assim usar a soma dos inversos. Ex:
Req = ?
Req = U/i
Req = 12/1
Req = 12 Ω
U = 12 V
i=1A
2. Página 338.
a) em série.
b) em paralelo.
c) A resistência equivalente dos resistores que estão em paralelo. (nos ramos dos resistores R2 e R3); Para evitar a
soma dos inversos acharemos a intensidade dos dois ramos usando a 1ª Lei de Ohm e depois achamos sua
resistência total.
1º passo: intensidade do circuito de R2:
R2 = 10 Ω
R = U/i
10 = 100/i
10 . i = 100
i = 100/10
i = 10 A
U = 100 V
i=?
2º passo: intensidade do circuito de R3:
R3 = 15 Ω
R = U/i
15 = 100/i
15 . i = 100
i = 100/15
i = 6,66 A
U = 100 V
i=?
3º passo: intensidade total dos circuitos de R2 e R3: ieq = i de R2 + R3 (em circuitos paralelos a intensidade se somam)
i de R2 = 10 A
i = 10 + 6,66 i = 16,66 A
i de R3 = 6,66 A
4º passo: Agora achamos a resistência total destes dois ramos usando a 1ª Lei de Ohm.
Req = ?
R = U/i
Req = 100/16,66
Req = 6 Ω
i = 16,66 A
U = 100 V
Obs: Poderia ter resolvido através dos inversos.
1/R2-3 = 1/R2 + 1/R3
1/R2-3 = 1/10 +1/15
1/R2-3 = (15 + 10)/150
1/R2-3 = 25/150
1/R2-3 = 1/6 R2-3 = 6 Ω
d) Resistência total do circuito. Ao calcularmos a resistência de R2 e R3, transformamos o circuito numa associação de
resistores em série. A Req de um circuito em série é igual a sua soma de seus resistores. Req = R1 + (R2 + R3) R4
Req = 12 + 6 + 22
Req = 40 Ω
e) A intensidade total da corrente no circuito é: Se temos a tensão e resistência total, basta usar a 1ª Lei de Ohm.
Req = 40 Ω
R = U/i
40 = 100/i
40 . i = 100
i = 100/40
i = 2,5 A
U = 100 V
i=?