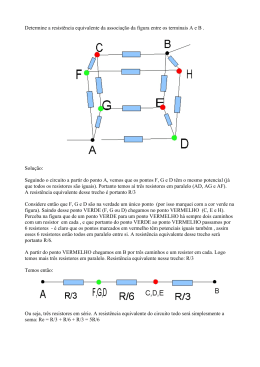
ELETRICIDADE 1 – CAPÍTULO 3
RESISTORES E RESISTÊNCIAS
No Capítulo 2 estudamos, dentre outras coisas, o conceito de resistência elétrica. Vimos que tal
constitui a capacidade de um corpo qualquer se opôr a passagem de uma corrente elétrica pelo mesmo,
quando este for submetido a uma diferença de potencial elétrico. Nos circuitos elétricos e eletrônicos, em
geral, as resistências são caracterizadas por dispositivos denominados resistores.
Resistores
Um resistor constitui um dispositivo que tem por finalidade apresentar uma determinada resistência
elétrica, a partir do material empregado, que pode ser, por exemplo, carbono. Alguns resistores são longos e
finos, com o material resistivo colocado ao centro, e um terminal de metal ligado em cada extremidade. Este
tipo de encapsulamento é denominado axial. A Figura 3.1 mostra, como modelo, alguns resistores comerciais
usados nos circuitos elétricos e eletrônicos.
Figura 3.1 – Grupo de resistores.
Os resistores usados em computadores e outros dispositivos são tipicamente muito menores. Nestes,
freqüentemente são utilizadas tecnologias de montagem superficial (Surface-mount technology), ou seja,
SMT. Esse tipo de resistor não tem “perna” de metal (denominada terminal). Resistores de maiores potências
são produzidos de forma robusta para dissipar calor com maior eficiência, embora sigam basicamente a
mesma estrutura. Cabe mencionar que o resistor, bem como a resistência em si, são dispositivos não
polarizados, isto é, sem um lado (terminal) específico para ser conectado no positivo (+) ou negativo (−) de
um circuito ou fonte de fem.
Resistor Variável
Os resistores discutidos acima são denominados fixos, pois seu valor não pode ser ajustado/variado.
Porém, existem também os denominados resitores variáveis. Estes são aqueles cujo valor pode ser ajustado
por um movimento mecânico como, por exemplo, rodando manualmente uma alavanca, também denominada
cursor. Os resistores variáveis podem ser de volta simples ou de múltiplas voltas, com um elemento
helicoidal. Abaixo é mostrada a simbologia de um resistor variável.
Tradicionalmente, resistores variáveis não são confiáveis. Isto porque o fio ou o metal que o constitui
pode corroer ou se desgastar. Alguns resistores variáveis modernos usam materiais plásticos que não
1
corroem. Outro método de controle envolve um sistema com sensor fotoelétrico que mede a densidade ótica
de um pedaço de filme. Desde que o sensor não toque o filme, é impossível haver desgaste do resistor. Os
resitores variáveis podem ser agrupados em potenciômetros (também denominados reostatos) ou trimpots.
O potenciômetro, mostrado na Figura 3.2, é um tipo de resistor variável comumente utilizado para
controlar o volume em amplificadores de áudio. É um resistor de três terminais onde a conexão central, além
de deslizante, é facilmente manipulável/ajustável.
Figura 3.2 – Potenciômetro.
O trimpot (do inglês trimmer potentiometer), mostrado na Figura 3.3, é um potenciômetro miniatura
de “calibre”. O mesmo é um resistor ajustável. Porém, quando instalado em algum dispositivo/circuito, este
normalmente fica em local de difícil acesso ao usuário. Assim, eventuais ajustes deste acabam, em geral,
sendo feitos somente por técnicos. Esses ajustes são comuns em circuitos de precisão, como componentes de
áudio ou vídeo, e podem necessários quando o aparelho é consertado. Isto justifica o termo calibre (é mais
conveniente dizer que o trimpot é calibrado ao invés de ajustado), pois o acesso ao mesmo dá-se apenas em
situações especiais (consertos, manutenção, etc), diferentemente do potenciômetro, o qual é manipulado
freqüentemente. Ao contrário de outros controles variáveis, os trimpots são montados diretamente na placa
de circuito, ajustados por uma pequena chave, e projetados para uma grande quantidade de pequenos ajustes
em sua vida útil.
Figura 3.3 – Aspecto dos trimpots.
Código de Cores para Resistores de Quatro Faixas
A Figura 3.1 mostrou um conjunto de resistores fixos de pequena potência (em geral, 1/8W ou
1/4W). Suponhamos, então, agora, que vamos sortear um deles e observá-lo mais de perto. Assim sendo,
teríamos uma visão do resistor escolhido tal como na Figura 3.4, abaixo.
Figura 3.4 – Da esquerda para a direita, temos a 1ª, 2ª, 3ª e 4ª faixa (os anéis).
2
Observando esse resistor, verificamos que o mesmo apresenta quatro faixas em seu invólucro. Essas
faixas são coloridas. Da esquerda para a direita, na Figura 3.4, as três primeiras faixas estão bem próximas
umas das outras, ao passo que a quarta e última faixa localiza-se mais distanciada da terceira, e próxima da
extremidade direita do componente. Essas (quatro) faixas coloridas mencionadas têm a finalidade de
expressar o valor da resistência ôhmica deste resistor. A Figura 3.5 exibe/esquematiza com mais detalhes as
características mencionadas a respeito da Figura 3.4 e do código de cores.
Figura 3.5 – Código de cores para resistores de quatro faixas.
Existem basicamente duas opções para conhecer o valor de um resistor. Uma destas maneiras
consiste em medir o valor de um resistor com um ohmímetro, sendo este o aparelho usado para efetuar a
medida de uma determinada resistência. O mesmo é dotado de duas “ponteiras”. Para tanto, cada uma destas
ponteiras deve ser conectada a cada um dos extremos da resistência. Neste caso, dizemos que o ohmímetro
está conectado em paralelo com a resistência (o termo paralelo ficará mais claro no capítulo sobre circuitos
elétricos). Além disso, a resistência deve estar desconectada do circuito ao qual esta faz parte. Maiores
detalhes sobre o funcionamento do ohmímetro serão vistos mais adiante, no capítulo que trata sobre circuitos
elétricos. Uma outra alternativa para se conhecer o valor de um resistor consiste em ler o seu valor
diretamente no seu invólucro. Esta opção é a mais eficaz. Para tanto, é necessário conhecer o código de cores
que possibilitará a leitura desses valores de resistência.
O código de cores, identificado na Tabela 3.1, é a convenção utilizada para identificação de
resistores de uso geral. Compreende os resistores das séries E6, E12 e E24 (20%, 10% e 5% de tolerância,
respectivamente) da norma internacional IEC (International Electrotechnical Commission). Primeiro,
veremos o caso dos resistores com quatro faixas coloridas.
Cores
Preto
Marrom
Vermelho
Laranja
Amarelo
Verde
Azul
Violeta
Cinza
Branco
Prata
Ouro
Sem cor
1ª faixa
0
1
2
3
4
5
6
7
8
9
-
2ª faixa
0
1
2
3
4
5
6
7
8
9
-
3ª faixa
×100 = ×1
×101 = ×10
×102
×103
×104
×105
×106
×107
×108
×109
−2
×10 = ×0,01
×10−1 = ×0,1
-
4ª faixa
±10%
±5%
±20%
Tabela 3.1 – Código de cores para resistores de quatro faixas.
Procedimento para Determinar o Valor dos Resistores de Quatro Faixas Via Código de Cores
Para determinar o valor ôhmico da resistência de um resistor codificado em quatro faixas coloridas,
utilizemos a Figura 3.4 e a Tabela 3.1. Observemos o resistor da Figura 3.4, tal como este aparece nela: da
esquerda para a direita, as três primeiras faixas, próximas umas das outras; ao passo que a quarta e última
3
faixa localiza-se mais distanciada da terceira, próxima da extremidade direita. Então, nessa seqüência,
devemos:
I.
Identificar a cor do primeiro anel, e verificar através da tabela de cores o algarismo correspondente à
cor. Este algarismo (significativo) será o primeiro dígito do valor do resistor.
II. Identificar a cor do segundo anel, e verificar através da tabela de cores o algarismo correspondente à
cor. Este algarismo (significativo) será o segundo dígito do valor do resistor.
III. Identificar a cor do terceiro anel, e verificar através da tabela de cores o algarismo (significativo)
correspondente à cor pela primeira (ou segunda) faixa (anel). Esse número será o expoente de um
fator multiplicativo de uma potência de base dez, tal como ilustra a coluna “3ª Faixa”, na Tabela 3.1.
Então, deve-se multiplicar o número formado pelos itens I e II (uma dezena, especificamente) por
este fator de potência para, então, obter o valor nominal (ideal) ôhmico da resistência. Este anel é
também conhecido como multiplicador. Atenção especial se deve ter com as cores ouro e prata nessa
faixa. Quando esta faixa for de cor dourada, o valor nominal da resistência estará dentro de uma
dezena de ohms, isto é, entre 0Ω e 10Ω. Quando esta faixa for de cor prata, o valor nominal da
resistência será menor que um ohm; em outras palavras, estará dentro de centenas de miliohms.
IV. Identificar a cor do quarto anel, verificando a coluna “4ª Faixa”, na Tabela 3.1, para a determinação
da porcentagem de tolerância do valor nominal da resistência do resistor (nota: a ausência do quarto
anel indica a tolerância de ±20%). Este percentual indica o quanto o valor real da resistência poderá
ser para mais, ou para menos, do valor nominal determinado pelos itens anteriores. Este anel é
também conhecido como tolerância.
Como um rápido exemplo, consideremos que: 1ª Faixa = Vermelha = 2; 2ª Faixa = Violeta = 7; 3ª
Faixa = Amarelo = 4; e a 4ª Faixa = Ouro = ±5%. Assim sendo, o valor do resistor será de (27×104Ω)±5% =
270000Ω±5% = 270kΩ±5%. Logo, o valor será 270kΩ com 5% de tolerância. Ou seja, o valor exato da
resistência para qualquer elemento com esta especificação estará entre 256,5kΩ (5% abaixo do valor nominal
270kΩ) e 283,5kΩ (5% acima do valor nominal 270kΩ). Vemos que o multiplicador consiste no número de
zeros que você coloca na frente do número (dezena) formado pelos itens I e II. No exemplo, a terceira faixa
(anel) é o amarelo, de valor 4. Logo, você coloca quatro zeros após o número (dezena) formado pelos itens I
e II; se a terceira faixa fosse o Vermelho = 2, você colocaria dois zeros; e se fosse o preto = 0, você não
colocaria nenhum zero, o que equivale a multiplicar o número (dezena) formado pelos itens I e II por 1.
Um elemento que talvez necessite explicação mais apurada é a tolerância. O processo de fabricação
em massa de resistores não consegue garantir, para estes componentes, um valor exato de resistência. Assim,
pode haver variação dentro do valor especificado de tolerância. É importante notar que quanto menor a
tolerância, mais caro o resistor, pois o processo de fabricação deve ser mais refinado para reduzir a (mínima)
variação em torno do valor nominal. Caso contrário, o teste dos resistores pelo fabricante rejeitaria mais
componentes, elevando, assim, o custo de produção.
Resistores de Cinco Faixas
Em algumas aplicações, são necessários resistores com valores mais precisos. Então, são usados
resistores os quais podem apresentar até cinco faixas coloridas. Nesses resistores, as três primeiras faixas são
dígitos significativos, a quarta faixa representa o número de zeros e a quinta faixa é então a tolerância. Como
um rápido exemplo, consideremos: 1ª Faixa = Vermelha = 2; 2ª Faixa = Violeta = 7; 3ª Faixa = Verde = 5; 4ª
Faixa = Amarelo = 4; e a 5ª Faixa = Ouro = ±5%. Assim sendo, o valor do resistor será de (275×104Ω)±5% =
2.750.000Ω±5% = 2,75MΩ±5%.
Valores Comerciais de Resistores
Existem três séries de resistores comerciais. Cada série tem seus valores padrão, dos quais o valor
indicado em um resistor, via código de cores, será múltiplo ou submúltiplo deste (função esta desempenhada
pela terceira faixa, no caso dos resistores de quatro faixas; e pela quarta faixa, no caso dos resistores de cinco
faixas). Tais valores padrão são aqueles formados pela combinação dos algarismos significativos (da
primeira e da segunda faixa, no caso dos resistores de quatro faixas; e da primeira, segunda e terceira faixa,
no caso dos resistores de cinco faixas). Não vamos listar aqui todos estes, mas apenas os valores padrão da
4
primeira série de resistores comerciais. Isto porque estes são de uso mais geral, sobretudo na eletrônica. Os
valores padrão da primeira série de resistores (5%, 10% e 20% de tolerância) são: 10, 12, 15, 18, 22, 27, 33,
39, 47, 56, 68 e 82.
EXEMPLOS
1. Determine o valor ôhmico dos seguintes resistores de quatro faixas, mostrados abaixo, através da sua
codificação em cores:
a)
b)
c)
d)
e)
f)
Marrom, vermelho, marrom, prata.
Laranja, laranja, vermelho, prata.
Amarelo, violeta, verde, dourado.
Laranja, branco, dourado, dourado.
Amarelo, violeta, prata.
Marrom, preto, vermelho.
2. Determine a codificação em cores para os seguintes resistores de quatro faixas abaixo:
a)
b)
c)
d)
e)
f)
10Ω±10%.
820Ω±10%.
1,2kΩ±5%.
3,9MΩ±10%.
2R2±20%.
0R56±5%.
Associação de Resistências
Na prática, em circuitos elétricos e eletrônicos, em geral, é freqüente o uso de resistores associados
em série, ou em paralelo, ou de maneira mista (misturando as configurações série e paralelo). O conceito de
associação de resistências dá-se no estudo de circuitos elétricos, o qual faremos em um capítulo adiante. Por
uma questão de simplicidade, o façamos com antecedência.
Associação de Resistências em Série
A associação de resistências em série é feita conforme mostra a Figura 3.6.
Figura 3.6 – Associação de resistências em série.
Ligando-se o ohmímetro (aparelho cuja simbologia corresponde a um círculo com a unidade de
medida de resistência, Ω, inscrita no mesmo) entre os extremos da combinação de resistências em série, o
mesmo indicará o valor da resistência equivalente dessa combinação. O conceito de resistência equivalente
5
será mais bem entendido no estudo de circuitos elétricos, mais adiante. Por hora, podemos dizer que a
resistência equivalente (Req) é aquela (resistência única) de valor tal que pode substituir, por completo, uma
combinação resistiva, seja esta do tipo série, ou paralela, ou mista. Portanto, pela Figura 3.6, generalizando o
resultado obtido acima para n resistências associadas em série, conclui-se que
n
Req = ∑ R j = R1 + R2 + R3 + ... + Rn .
(3.1)
j =1
Logo, a resistência equivalente (Req), referente a uma associação em série de resistências,
corresponderá à soma dos valores das resistências usadas na associação. Assim, em uma associação de
resistências em série, a resistência equivalente é sempre maior que a maior resistência dentre aquelas usadas
na referida associação.
Para o caso especial em que todas as resistências usadas na associação série tenham o mesmo valor
ôhmico ideal, podemos determinar, via (3.1), que a resistência equivalente, neste caso, seja dada por
Req = n ⋅ R ,
(3.2)
onde R é o valor comum de resistência ôhmica usada na associação e n o número de resistências (iguais)
dessa associação.
Associação de Resistências em Paralelo
A associação de resistências em paralelo é feita conforme mostra a Figura 3.7.
Figura 3.7 – Associação de resistências em paralelo.
Na Figura 3.7, podemos perceber que um lado (terminal) de cada uma das n resistências da
associação estão conectados na linha superior horizontal, e o outro lado, então, na linha inferior horizontal.
Estas conexões são denominadas nós ou junções (que correspondem aos pontos escuros e ressaltados). O
conceito de nó, ou junção, será mais bem entendido no capítulo que aborda o estudo de circuitos elétricos.
Por hora, no entanto, podemos apenas afirmar que nó é um ponto (comum) onde os terminais de diversos
condutores se conectam.
Pela Figura 3.7, generalizando o resultado obtido acima para n resistências associadas em paralelo,
conclui-se que
n
1
1
1
1
1
1
=∑
=
+
+
+ ... +
.
Req
R1 R2 R3
Rn
j =1 R j
(3.3)
Logo, o inverso da resistência equivalente (Req), referente a uma associação em paralelo de
resistências, corresponderá à soma dos inversos dos valores das resistências usadas na referida associação.
Assim, em uma associação de resistências em paralelo, a resistência equivalente é sempre menor que a
menor resistência dentre aquelas usadas na associação. Ainda, às vezes, (3.3) pode aparecer na forma
6
Req =
1

∑ 1
 j =1 R
j

n




=
1
 1
1
1
1 
 +

+
+ ... +
Rn 
 R1 R2 R3
,
(3.4)
a qual diz que a resistência equivalente (Req), referente a uma associação em paralelo de resistências,
corresponderá ao inverso da soma dos inversos dos valores das resistências usadas na referida associação.
Para o caso especial em que todas as resistências usadas na associação paralela tenham o mesmo
valor ôhmico ideal, podemos determinar, via (3.3) ou (3.4), que a resistência equivalente, neste caso, seja
dada por
Req =
R
,
n
(3.5)
onde R é o valor comum de resistência ôhmica usada na associação e n o número de resistências (iguais)
dessa associação.
Para o caso especial de duas resistências associadas em paralelo, há uma relação bastante útil,
derivada do somatório (3.3), e expressa matematicamente na seguinte forma:
Req =
R1 ⋅ R2
.
R1 + R2
(3.6)
EXEMPLOS
3. Duas resistências, R1 = 6Ω e R2 = 4Ω, são associadas em série. Qual o valor da resistência
equivalente desta associação?
4. Considere que você tenha em mãos uma resistência de valor igual a 3Ω. Sendo assim, pede-se para
determinar o valor da resistência que se deve colocar em série com esta (de 3Ω) a fim de que a
resistência equivalente do conjunto seja igual a 10Ω.
5. Suponha que você queira associar em série 100 resistores com resistência de 6,8Ω cada. Assim
sendo, determine a resistência equivalente desse conjunto.
6. Resolva o exemplo 3 considerando que as resistências R1 e R2 estejam associadas em paralelo.
7. Três resistências, R1 = 6Ω e R2 = 4Ω e R3 = 2Ω, são associadas em paralelo. Qual o valor da
resistência equivalente desta associação?
8. Suponha que você queira associar em paralelo 200 resistores com resistência de 18kΩ cada. Assim
sendo, determine a resistência equivalente desse conjunto.
9. Determine a resistência que se deve colocar em paralelo com uma outra de 24Ω a fim de que a
resistência equivalente do conjunto se reduza a 8Ω.
10. Determine o valor da resistência que se deve colocar em paralelo com outra de 4Ω a fim de que a
resistência equivalente do conjunto se reduza a um oitavo do valor da resistência equivalente que
seria obtida pela associação em série das mesmas.
Associação Mista de Resistências
7
A associação mista de resistências é aquela que mistura resistências associadas em série e também
em paralelo.
EXEMPLOS
11. Determine a resistência equivalente da associação resistiva indicada abaixo.
R1 = verde, preto, dourado
R2 = amarelo, preto, dourado
R3 = R5 = R6 = vermelho, preto, dourado
R4 = marrom, preto, dourado
Observação: Despreze as “tolerâncias” das resistências para os cálculos nesse último item.
EXERCÍCIOS PROPOSTOS
1. Determine o valor ôhmico dos seguintes resistores de quatro faixas, mostrados abaixo, através da sua
codificação em cores:
a)
b)
c)
d)
e)
f)
g)
Azul, cinza, vermelho, prata.
Vermelho, vermelho, verde, prata.
Verde, azul, preto, dourado.
Laranja, branco, marrom, dourado.
Amarelo, violeta, azul.
Marrom, cinza, prata.
Cinza, vermelho, dourado, dourado.
2. Determine a codificação em cores para os seguintes resistores de quatro faixas abaixo:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
470Ω±10%.
270Ω±5%.
560Ω±10%.
1,8kΩ±10%.
820Ω±20%.
12kΩ±5%.
6R8±20%.
220kΩ±10%.
2,7MΩ±5%.
27MΩ±5%.
0R39Ω±20%.
15Ω±20%.
3. Duas resistências, R1 = 2Ω e R2 = 8Ω, são associadas em série. Qual o valor da resistência
equivalente desta associação?
4. Considere que você tenha em mãos uma resistência de valor igual a 9Ω. Sendo assim, pede-se para
determinar o valor da resistência que se deve colocar em série com esta (de 9Ω) a fim de que a
resistência equivalente do conjunto seja igual a 10Ω.
8
5. Suponha que você queira associar em série 5.000 resistores com resistência de 12Ω cada. Assim
sendo, determine a resistência equivalente desse conjunto, em quilo-ohm (kΩ).
6. Quantos resistores com resistência de 18Ω são necessários para serem associados em série com
vistas a obtermos uma resistência equivalente de 5,4kΩ?
7. Resolva o exercício 3 considerando que as resistências R1 e R2 estejam associadas em paralelo.
8. Três resistências, R1 = 12Ω e R2 = 8Ω e R3 = 4Ω, são associadas em paralelo. Qual o valor da
resistência equivalente desta associação?
9. Suponha que você queira associar em paralelo 5.000 resistores com resistência de 1,8MΩ cada.
Assim sendo, determine a resistência equivalente desse conjunto.
10. Quantos resistores com resistência de 2,7kΩ são necessários para serem associados em paralelo com
vistas a obtermos uma resistência equivalente de 12Ω?
11. Determinar a resistência que se deve colocar em paralelo com uma outra de 12Ω a fim de que a
resistência equivalente do conjunto se reduza a 4Ω.
12. Determine o valor da resistência que se deve colocar em paralelo com outra de 4Ω a fim de que a
resistência equivalente do conjunto se reduza a metade da diferença entre a resistência desconhecida
e a de 4Ω. Dica: lembre da fórmula de Bhaskara!
13. Determine a resistência equivalente da associação resistiva indicada abaixo.
R1 = R2 = 6Ω
R3 = R4 = 4Ω
14. Determine a resistência equivalente da associação resistiva indicada no diagrama abaixo.
R1 = marrom, vermelho, vermelho, dourado
R2 = laranja, laranja, vermelho, dourado
R3 = vermelho, violeta, preto, dourado
R4 = laranja, branco, marrom, dourado
Observação: Despreze as “tolerâncias” das resistências nos
cálculos dessa questão.
15. Determine a resistência equivalente da associação resistiva indicada no diagrama abaixo.
R1 = laranja, branco, amarelo, dourado
R2 = marrom, verde, amarelo, dourado
R3 = marrom, preto, laranja, dourado
R4 = marrom, vermelho, azul , dourado
Observação: Despreze as “tolerâncias” das resistências nos
cálculos dessa questão.
9
16. Determine a resistência equivalente da associação resistiva indicada no diagrama abaixo.
R1 = R2 = amarelo, violeta, amarelo, dourado
R3 = azul , cinza, vermelho, dourado
R4 = amarelo, violeta, vermelho, dourado
Observação: Despreze as “tolerâncias” das resistências nos cálculos dessa questão.
17. Determine a resistência equivalente da associação resistiva indicada no diagrama abaixo.
R1 = R2 = marrom, vermelho, amarelo, dourado
R3 = laranja, branco, amarelo, dourado
R4 = marrom, cinza, amarelo, dourado
Observação: Despreze as “tolerâncias” das resistências nos
cálculos dessa questão.
18. Determine a resistência equivalente da associação resistiva indicada no diagrama abaixo.
R1 = R2 = R6 = R8 = vermelho, preto, preto, dourado
R3 = R7 = R13 = R16 = amarelo, preto, preto, dourado
R4 = R5 = marrom, preto, preto, dourado
Observação:
Despreze as “tolerâncias” das resistências
nos cálculos dessa questão.
R9 até R12 = azul , preto, preto, dourado
R14 = R15 = laranja, preto, preto, dourado
10
19. Duas resistências, R1 = 6Ω e R2 de valor desconhecido, são ligadas em paralelo e, em seguida, uma
terceira resistência R3, valendo o dobro da primeira, é ligada em série com esta combinação,
formando, então, uma associação resistiva mista de 14Ω. Determine o valor da resistência R2.
20. Duas resistências, R1 = 6Ω e R2 de valor desconhecido, são ligadas em série e, em seguida, uma
terceira resistência R3, valendo o dobro da primeira, é ligada em paralelo com esta combinação série,
formando, então, uma associação resistiva mista de 10Ω. Determine o valor da resistência R2.
RESPOSTAS DOS EXERCÍCIOS PROPOSTOS
1. a) 6,8kΩ±10%; b) 2,2MΩ±10%; c) 56Ω±5%; d) 390Ω±5%; e) 47MΩ±20%; f) 0,18Ω±20%;
g) 8,2Ω±5%.
2. a) amarelo, violeta, marrom, prata; b) vermelho, violeta, marrom, dourado; c) verde, azul, marrom,
prata; d) marrom, cinza, vermelho, prata; e) cinza, vermelho, marrom, sem cor; f) marrom,
vermelho, laranja, dourado; g) azul, cinza, dourado, sem cor; h) vermelho, vermelho, amarelo, prata;
i) vermelho, violeta, verde, dourado; j) vermelho, violeta, azul, dourado; k) laranja, branco, prata,
sem cor; l) marrom, verde, preto, sem cor.
3. 10Ω.
4. 1Ω.
5. 60kΩ.
6. 300 resistores.
7. 1,6Ω.
8. 2,18Ω.
9. 360Ω.
10. 225 resistores.
11. 6Ω.
12. 9,66Ω.
13. 12,4Ω.
14. 4.525,25Ω.
15. 377,88kΩ.
16. 237,78kΩ.
17. 168,89kΩ.
18. 100Ω.
19. 3Ω.
20. 54Ω.
11
EXERCÍCIOS PROPOSTOS – Usando o protoboard
1. Determine a resistência equivalente da associação resistiva indicada nos diagramas dos itens abaixo
de duas maneiras: (1) Por meio de cálculos e (2) montando os circuitos no protoboard, usando os
resistores (da lista de materiais). Verifique o resultado obtido, no passo (2), por meio do multímetro
(este último atuando como ohmímetro). Compare, então, os resultados obtidos, pelos passos (1) e
(2), entre si. Procure entender as diferenças encontradas.
a) Diagrama 1:
R1 = amarelo, violeta, preto
R2 = verde, azul , preto
R3 = marrom, preto, marrom
R4 = marrom, verde, marrom
R5 = vermelho, vermelho, marrom
R6 = vermelho, violeta, marrom
Observação: Despreze as “tolerâncias” das resistências para os cálculos nesse último item.
b) Diagrama 2:
R1 = laranja , branco, marrom
R2 = verde, azul , marrom
R3 = amarelo, violeta, preto
R4 = verde, azul , preto
R5 = marrom, preto, marrom
R6 = marrom, verde, marrom
Observação: Despreze as “tolerâncias”
resistências nos cálculos dessa questão.
das
c) Diagrama 3:
R1 = amarelo, violeta, preto
R2 = verde, azul , preto
R3 = marrom, preto, marrom
R4 = marrom, verde, marrom
R5 = vermelho, vermelho, marrom
R6 = vermelho, violeta, marrom
R7 = laranja, branco, marrom
R8 = verde, azul , marrom
R9 = laranja, laranja, laranja
Observação: Despreze as “tolerâncias” das resistências nos cálculos dessa questão.
12