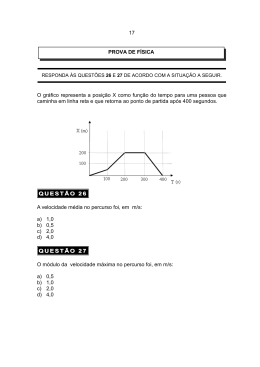
Trabalho de Expansão
Vamos discutir a expressão matemática da quantidade de energia trocada
entre um sistema e sua vizinhança quando o volume do sistema varia. Assim, vamos
supor que o sistema tem uma pequena variação de volume ∆V, passando de V para V
+ ∆V sob o efeito de uma pressão externa Pe. Aqui devemos observar que se ∆V é
positivo, o volume do sistema aumenta e se ∆V é negativo, o volume do sistema
diminui.
A cada elemento de superfície ∆S da fronteira do sistema associamos um vetor
∆A, de módulo igual à área do elemento de superfície, direção perpendicular a ele e
sentido de dentro para fora (Fig.46(a)).
A força externa que atua sobre um elemento de superfície da fronteira do
sistema pode ser escrita:
∆Fe = − Pe ∆A
O sinal negativo indica que esta força externa tem sentido contrário ao vetor
∆A (Fig.46(b)).
Se esse elemento de superfície tem um deslocamento infinitesimal ∆d, a
correspondente quantidade de energia trocada entre o sistema e a vizinhança, relativa
ao trabalho associado a esta força externa, é:
∆W*e = ∆Fe ⋅ ∆d = − Pe ∆A ⋅ ∆d
Quando levamos em conta todos os elementos de superfície da fronteira do
sistema, a correspondente quantidade de energia trocada entre o sistema e a
vizinhança, relativa ao trabalho associado às forças externas, é:
∆W e = Σ ∆W*e = − Pe ( Σ ∆A ) ⋅ ∆d = − Pe ( Σ ∆A ) ∆d = − Pe A∆d
ou
∆W e = − Pe ∆V
Grupo de Ensino de Física da Universidade Federal de Santa Maria
em que Σ representa a soma sobre todos os elementos de superfície e A representa a
área da fronteira do sistema. Nesse ponto, devemos observar o seguinte:
• Quando ∆V > 0, o sistema se expande. Então, ∆W e < 0 e a energia flui do
sistema para a vizinhança.
• Quando ∆V < 0, o sistema se contrai. Então, ∆W e > 0 e a energia flui da
vizinhança para o sistema.
Até agora consideramos a variação de volume ∆V do sistema como sendo
pequena. Assim, a quantidade de energia ∆W e trocada entre o sistema e a vizinhança
também é pequena. Agora vamos considerar uma variação de volume de qualquer
magnitude (finita). Qualquer variação finita de volume pode ser pensada como uma
seqüência de pequenas variações de volume, de modo que a correspondente
quantidade de energia trocada entre o sistema e a vizinhança, relativa ao trabalho
associado às forças externas, é dado pela soma We = Σ ∆W e, ou seja:
We = − Σ Pe ∆V
Por outro lado, pela terceira lei de Newton, as forças do sistema sobre a
vizinhança são iguais em módulo e direção, mas de sentido contrário, às forças
externas que atuam sobre o sistema. Portanto, podemos representar a quantidade de
energia trocada entre o sistema e a vizinhança relativamente ao trabalho associado às
forças do sistema sobre a vizinhança pela expressão:
W = Σ Pe ∆V
Esta expressão é geral. Aqui é bom lembrar que Pe representa, ainda, a
pressão externa (da vizinhança) sobre o sistema. Contudo, se o processo de variação
do volume do sistema é reversível, tem sentido falar na pressão P do sistema e mais,
em todos os estados pelos quais passa o sistema no processo de variação de volume,
a pressão do sistema é igual à pressão externa. Portanto, se a variação de volume é
pequena podemos escrever:
∆W = P∆V
(processo reversível)
Nesse ponto, devemos observar o seguinte:
• Quando ∆V > 0, o sistema se expande. Então, ∆W > 0 e a energia flui do
sistema para a vizinhança.
• Quando ∆V < 0, o sistema se contrai. Então, ∆W < 0 e a energia flui da
vizinhança para o sistema.
Se a variação de volume do sistema tem magnitude (finita):
W = Σ P∆V
(processo reversível)
A vantagem desta expressão sobre a expressão W = Σ Pe ∆V é que podemos
calcular o somatório do lado direito se conhecemos a equação de estado do sistema,
ou seja, se conhecemos a expressão matemática que relaciona a pressão e o volume.
Grupo de Ensino de Física da Universidade Federal de Santa Maria
Processo Isobárico Reversível
Se o volume do sistema varia de V1 para V2 por um processo isobárico e
reversível, com o sistema sendo mantido a uma pressão P0 (Fig.47), temos:
W = Σ P∆V = P0 Σ ∆V = P0 ( V2 − V1 )
Esse resultado mostra que a quantidade de energia que o sistema troca com a
vizinhança corresponde à área entre o gráfico do processo isobárico no plano PV e o
eixo dos volumes entre V1 e V2.
No caso particular em que o sistema é formado por uma amostra de gás ideal:
W = PV2 − PV1 =nR ( T2 − T1 )
Processo Isotérmico Reversível
A quantidade de energia trocada entre o sistema formado por uma amostra de
gás ideal e a vizinhança, no caso em que o volume do sistema varia de V1 para V2 por
um processo isotérmico reversível (Fig.48), é dada pela expressão:
V
W = nRT ln  2
 V1



Grupo de Ensino de Física da Universidade Federal de Santa Maria
Observação
No caso do processo isobárico reversível, concluímos que a quantidade de
energia que o sistema troca com a vizinhança, em correspondência ao trabalho
associado às forças do sistema sobre a vizinhança, é dada pela área entre o gráfico
do processo no plano PV e o eixo dos volumes entre V1 e V2. Essa conclusão é de
caráter geral, isto é, vale para todos os processos reversíveis. A partir dessa
interpretação, podemos entender que a quantidade de energia mencionada depende
do processo que liga os estados inicial e final porque áreas diferentes estão
associadas a processos diferentes.
Exercício 1
Uma amostra de 1000 mol de gás ideal percorre reversivelmente, por 10 vezes,
o ciclo mostrado na Fig.49. (a) Calcule a quantidade de energia trocada por trabalho
entre a amostra de gás e a vizinhança. (b) Indique o sentido em que o ciclo deve ser
percorrido para que a quantidade de energia associada ao trabalho da amostra sobre
a vizinhança seja positiva.
Exercício 2
Um mol de gás ideal, inicialmente à temperatura de 300 K, é submetido ao
processo termodinâmico ABCD (Fig.50). Determine a quantidade de energia
associada ao trabalho do gás sobre a vizinhança nesse processo.
Grupo de Ensino de Física da Universidade Federal de Santa Maria
Exercício 3
Uma amostra de gás ideal à temperatura TA e à pressão PA é comprimida
reversivelmente até que seu volume fique reduzido à metade. A temperatura da
amostra de gás é alterada no processo, mas a relação P = kV, em que k é constante,
é satisfeita em todos os estados intermediários. (a) Represente o processo no
diagrama PV. (b) Determine, em termos de n, R e TA, a quantidade de energia
associada ao trabalho da amostra de gás sobre a vizinhança.
Exercício 4
Uma amostra de dois mols de um gás ideal tem pressão P1 = 2 atm e volume
V1 = 4 litros. Então, a temperatura da amostra é aumentada, a volume constante, até
que a pressão fique duplicada. Depois, a amostra é expandida isotermicamente até
que a pressão volte ao seu valor inicial. Finalmente, a amostra é comprimida, a
pressão constante, até que o seu volume volte ao valor inicial. (a) Represente todo
processo num diagrama PV. (b) Determine a quantidade de energia associada ao
trabalho da amostra de gás sobre a vizinhança em cada etapa do processo.
Grupo de Ensino de Física da Universidade Federal de Santa Maria