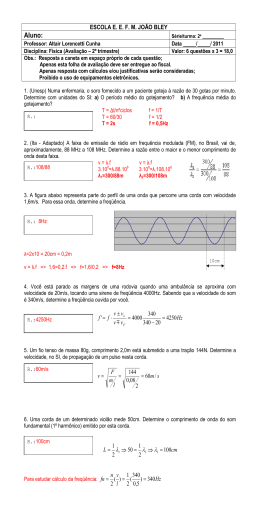
2º teste 4º exemplo
I Indução [7]
Considere o sistema de N=800 espiras quadradas de lado L=3cm, assente no plano XY, construídas com um fio muito fino
de modo que a sua espessura segundo Z pode ser
considerada desprezável face à dimensão L.
Espiras
com
R=1k 
Y
O valor da resistência do sistema de espiras
quadradas é R =1k 
L
𝑣
No instante inicial (t=0), o sistema de espiras está na
posição indicada na figura e move-se com velocidade
constante:
L
A
VR1
B
X
R2
R1
VR2
I


v  1 ey (cm s 1 )
R3
VR3
VR4
R4
Um circuito alimentado por uma fonte de tensão
contínua V0=80Volt, sendo Ri =4 k tem entre os
pontos A e B do circuito um fio longo AB >> L que
se encontra sobre o eixo dos XX. A resistência do fio
é desprezável face aos valores de Ri.
[2] a) Deduza a expressão analítica (vectorial) para
⃗ criado pela
o Campo de Indução Magnética 𝐵
corrente I que percorre AB, para x>0 e y > 0.
V0
[2]b) No instante t=1,5s determine o valor da intensidade da corrente induzida que percorre o sistema de espiras quadradas.
[2]c) No instante t=1,5s indique qual o sentido de circulação da corrente induzida que percorre o sistema de espiras quadradas.
[1] d) Para que a energia cinética do sistema de espiras quadradas seja constante terá de estar aplicada uma força que contrarie
a força magnética que sobre ele actua em cada instante. Determine para t=1,5s, o valor da potência mecânica aplicada.
Justifique o seu cálculo.
II- Circuitos em AC [5]
A fonte de tensão: V  V0 cos t está
V 
directamente aplicada a um circuito série
R
L
VL
indutor L
(Henry) e
resistência
R  1 k em que V0  311 Volt e
a frequência é de f
 10 kHertz .
[2]a) Determine a expressão analítica
do módulo da impedância do circuito
série-RL.
[2]b) Determine o valor da bobine
VR
L (Henry) sabendo que os voltímetros
VR e VL indicam precisamente o mesmo valor.
[1]c) Represente VL eff (Volt ) , VR eff (Volt ) e Veff (Volt ) num diagram de phasors.
2º teste 4ºexemplo
Técnico Lisboa Dep. Física
2014152S
I Ondas Electromagnéticas [8]
n0=1
Det 4
Considere o sistema óptico constituido
por uma lâmina de faces paralelas e por
um prisma de material dieléctrico (r=1)
de índices de refracção respectivamente
n1=n2=1,192, colocados conforme a
figura e cujo meio ambiente é o ar
(n0=nar  1).
E
n2=1,192
3
D
n0=1
Z
2
B
n1=1,192
A
n0=1
1
C
Note-se que a base do prisma (D) é
paralela à face (B) da lâmina de faces
paralelas.
Y
Uma (fonte) Onda Electromagnética
plana monocromática com =632,8nm
(medido no ar) ilumina em A a lâmina
de faces paralelas n 1, segundo o ângulo
0 (Brewster).
Det 3
Det 2
0
A onda reflectida em A será controlada
pelo detector Det1.
A onda transmitida em A irá viajar na
lâmina de faces paralelas e encontrará a
interface desta com o ar em B, onde incide
segundo o ângulo 1.
Det 1
A onda reflectida em B viajará até C onde incide segundo a perpendicular à face lateral da lâmina de faces paralelas
emergindo para o ar, sendo controlada pelo detector Det2.
A onda transmitida em B voltará a viajar no ar e atingirá em D a base do prisma, onde incide segundo o ângulo 2.
A onda reflectida em D será controlado pelo detector Det3.
A onda Transmitida em D atingirá a interface do prisma com o ar em E onde incide segundo a normal à face, emergindo
para o ar, sendo controlada pelo detector Det4.
Dados: 0= 4  x 10-7 NA-2 ; 0= 8,854x 10-12 Fm-1 ; 1/(40)= 9x109 mF-1 ; Z0=377
O Campo Eléctrico incidente no ponto B é dado por ( note o referencial XYZ com origem em A) :







Ex  a EB cos t  | k | (x  y  z )

E y  b EB sen t  | k | (x  y  z )

Ez  2 EB sen t  | k | (x  y  z )
[4]a) Determine o valor da constante a  de modo que a onda seja polarizada circular esquerda.
[2]b) Seja EB  5  103Vm 1 . Determine o valor das Amplitudes das componentes paralela e perpendicular do Campo
1

Eléctrico da onda medida no detector Det 1: E0 // Vm
1
e E Vm 
1
0
1
[2] c) Determine a razão das intensidades das componentes perpendiculares das ondas detectadas pelos detectores Det 2 e
Det 4, ou seja:   I 2 I 4 .
2º teste 4ºexemplo
Técnico Lisboa Dep. Física
2014152S