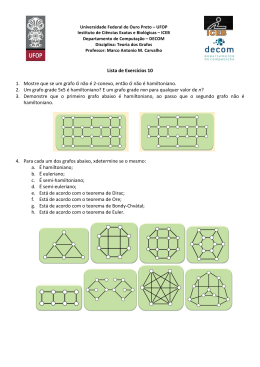
Introdução
Grafos
Grafos
Grafos
Prof. Dr. Julio Arakaki
www.pucsp.br/~jarakaki ([email protected])
Depto. Ciência da Computação
© Julio Arakaki
1
Ciência da Computação
Introdução
Grafos
Problema
Problema–– Abstração
Abstração–– Modelo
Modelo––Solução
Solução
Problema Real (Muitos)
Abstração (Análise do problema)
Modelagem
Grafos (Ferramenta de abstração)
Aplicação de algoritmos
Solução no domínio dos Grafos
© Julio Arakaki
2
Ciência da Computação
1
Introdução
Grafos
O
O que
queéé um
umGrafo?
Grafo?(formal)
(formal)
“Um grafo é representado como um conjunto de pontos
(vértices) ligados por retas (as arestas). Dependendo da
aplicação, as arestas podem ser direcionadas, e são
representadas por setas".
- Wikipédia -
© Julio Arakaki
3
Ciência da Computação
Introdução
Grafos
O
O que
queéé um
umGrafo?
Grafo?(mais
(maisinformal)
informal)
“Abstração que permite representar o relacionamento entre
pares de elementos“
Onde:
Elementos – vértices do grafo
(computadores, empresas, cidades, paises, pessoas, páginas
web, etc...)
Relacionamentos – arestas do grafo
(conexão, distância, amizade, custo, etc...)
© Julio Arakaki
4
Ciência da Computação
2
Introdução
Grafos
Exemplo
Exemplode
deGrafo:
Grafo:Tráfego
TráfegoRodoviário/Aéreo
Rodoviário/Aéreo
Transporte comercial entre cidades
Vôo entre as
cidades
São Paulo
Campo Grande
Rio de Janeiro
Brasília
Cuiabá
© Julio Arakaki
5
Ciência da Computação
Introdução
Grafos
Exemplo
Exemplode
deGrafo:
Grafo:Executando
Executandotarefas
tarefas
Tarefa
Relacionamento
entre tarefas:
“B depende de E”
- Todas as tarefas podem ser executadas?
-Qual a ordem de execução?
(Semelhante a um Sistema de N módulos com dependências
entre si – diversas bibliotecas.
Qual a seqüência/ordem de compilação ou execução dos
módulos?)
© Julio Arakaki
6
Ciência da Computação
3
Introdução
Grafos
Exemplo
Exemplode
deGrafo:
Grafo:PERT/CPM
PERT/CPM
“Program Evaluation and Review Technique” (PERT) e “Critical
Path Method” (CPM).
Para planejamento e controle de projetos (1950)
© Julio Arakaki
7
Ciência da Computação
Grafos
Introdução
Exemplo
Exemplode
deGrafo:
Grafo:Busca
Buscaem
em aplicativos
aplicativos P2P
P2P
O problema:
- os usuários rodam o aplicativo em suas
máquinas
- aplicativos se conectam formando uma rede
- usuários compartilham arquivos
Pergunta? Como encontrar os arquivos?
EXERCÍCIO: Criar a abstração do problema para um
modelo em grafo. Ou seja, criar um modelo indicando o
que são os vértices e as arestas para o problema acima?
© Julio Arakaki
8
Ciência da Computação
4
Introdução
Grafos
Exemplo
Exemplode
deGrafo:
Grafo:Busca
Buscaem
em aplicativos
aplicativos P2P
P2P
cslab1a
cslab1b
math.brown.edu
U1
A1
A2
A3
A4
U3
U2
cs.brown.edu
A5
A3
A4
brown.edu
qwest.net
att.net
U4
A1
A3
cox.net
John
Paul
David
© Julio Arakaki
9
Ciência da Computação
Introdução
Grafos
Exemplo
Exemplode
deGrafo:
Grafo:Outros
Outros
Sejam os seguintes domínios:
- Filmes e atores
- Relacionamentos nos sites de relacionamentos (Facebook,
LinkedIn, Orkut, ...)
- Rede de distribuição de energia
Robustez num sistema de transmissão de energia (Torres e
Linhas de Transmissão)
- Dê outros exemplos... (Circuito Impresso, Circuito Integrado, )
EXERCÍCIO: Criar os modelos em grafos, indicando o que é vértice e
aresta para os exemplos acima.
Quais são as perguntas que podem ser resolvidas com a modelagem
baseada em grafos?
© Julio Arakaki
10
Ciência da Computação
5
Introdução
Grafos
Início
Inícioda
dateoria
teoriade
de grafos:
grafos:as
as77 pontes
pontesde
deKönigsberg
Königsberg
A
B
D
C
Cidade de Königsberg (território da Prússia até 1945, atual Kaliningrado,
na Rússia), que é cortada pelo Rio Prególia, onde há duas grandes ilhas
que, juntas, formam um complexo que na época continha sete pontes.
- Wikipédia © Julio Arakaki
11
Ciência da Computação
Introdução
Grafos
As
As 77 pontes
pontes de
de Königsberg
Königsberg
Os habitantes da cidade, tentavam fazer um percurso
que os obrigasse a passar por todas as pontes, mas
apenas uma única vez.
As tentativas nunca deram certo, por isso, muitos
acreditavam que não era possível encontrar tal
percurso.
Será que tinham razão?
- Resolvido por Euler em 1736.
© Julio Arakaki
12
Ciência da Computação
6
Introdução
Grafos
As
As 77 pontes
pontes de
de Königsberg
Königsberg
Abstração via grafos:
A
Vértices – áreas de terra
Arestas – pontes
B
D
C
A
D
B
Existe o trajeto de percorrer
todas as pontes uma única vez
e retornar ao ponto inicial?
Resposta: NÃO.
Porque?
C
© Julio Arakaki
13
Ciência da Computação
Introdução
Grafos
Ciclo
CicloEuleriano
Euleriano
Percurso passando por todas as arestas uma única vez
e retornando ao ponto inicial:
- este percurso (ciclo) só existe se o grau dos
vértices for par. Onde, o grau de um vértice é o número
de arestas incidentes.
Para o exemplo:
A
D
B
A – grau 3
B – grau 5
C – grau 3
D – grau 3
Ou seja, não existe
Ciclo Euleriano
neste exemplo.
C
© Julio Arakaki
14
Ciência da Computação
7
Introdução
Grafos
Ciclo
CicloEuleriano
Euleriano
Teorema:
Um grafo G conexo, possui ciclo euleriano se e
somente se todo vértice de G possuir grau par.
Um grafo é conexo se existir caminho entre
quaisquer dois vértices.
© Julio Arakaki
15
Ciência da Computação
8