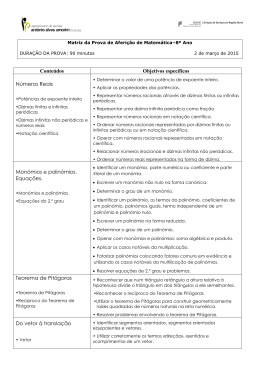
EB 2,3 de S. Paio – Moreira de Cónegos
Ficha de Avaliação de Matemática
8.º Ano de escolaridade
Janeiro/2008
INDICA TODOS OS CÁLCULOS QUE TIVERES QUE EFECTUAR
1. O João leu a história do professor Matema, na qual ele
construiu uma máquina dos monómios. Quando o professor
coloca um monómio na abertura da máquina, extrai-se um
monómio diferente, alterado pelas multiplicações indicadas.
O professor colocou na máquina o monómio, 4 a2.
1.1. Escreve o monómio que sairá da máquina, na forma
reduzida, indicando o coeficiente e a parte literal.
1.2. Qual o grau do monómio que se encontra na abertura da
máquina? E qual o grau do monómio extraído da máquina?
1.3. Escreve os monómios simétricos dos monómios que se
encontram, respectivamente, na entrada e saída, da máquina dos
monómios.
1.4. Determina o valor do monómio que se encontra na saída da
máquina, para a = 2 e b = - 3.
1.5. Que monómio teria que colocar o professor Matema na
abertura da máquina para que lhe saísse o monómio -4 a2 b3.
Explica como chegas-te á tua resposta. Podes fazê-lo utilizando
palavras, desenhos ou contas.
2. O livro da história do professor Matema conta que, um dia, ele construiu quatro robôs, o Tono, o
Sino, o Primo e o Dólio, de tal forma que:
- o Sino não é um Polinómio;
- o Tono e o Primo são Binómios;
- o Tono não é do 1.º grau.
-1-
http://hammermat.no.sapo.pt
2.1. Faz corresponder a cada letra, A, B, C ou D, que se encontra por baixo de cada um dos robôs,
o seu nome.
2.2. Se cada letra, A, B, C e D corresponder a expressão que se encontra em cada robô calcula com
a forma de Polinómio reduzido:
2.2.1. B + C;
2.2.2. C – A;
2.2.3. D × A.
2.3. Qual dos quadrados dos binómios corresponde ao trinómio C = a2 – 4a + 4:
(A) ( a + 2 )2
(B) ( 2 – a )2
(C) ( 2a – 2 )2
(D) ( 2 + 2a )2
3. O João reparou que no livro da história do professor Matema, que tem 150 páginas, aparecem
as seguintes figuras:
●
- Homem com as mãos erguidas;
●
- Sapo;
●
- Nenúfar.
As três figuras aparecem pela primeira vez e em simultâneo na página 21. Depois o João reparou
que o homem com as mãos levantadas reaparece de 12 em 12 páginas, o sapo reaparece de 15 em
15 páginas e o nenúfar de 10 em 10 páginas. Em que páginas voltam a estar representados as três
figuras em simultâneo?
Mostra como obtiveste a tua resposta.
4. Eis como, antigamente, os egípcios representavam os números 103 e 1,02 × 10 6:
10 3
=
1,02×10 6
4.1. Que número representa o símbolo
=
?
4.2. Representa o número 12 × 103, usando o menor número de símbolos egípcios.
4.3. Escreve, em notação científica, o número (1,02 × 10 6) ÷ (12 × 10 3).
4.4. Qual dos números não está compreendido entre 12 × 10 3 e 1,02 × 10 6.?
(A) 12,5 × 105
(B) 121 × 102
(C) 103 × 103
(D) 101500000 × 10-2
-2-
http://hammermat.no.sapo.pt
5. Na história do Professor Matema aparece o número de ouro (φ), este número tem propriedades
curiosas e o seu valor aproximado às décimas é o seguinte: φ ≈ 1,6.
Curioso, o João decidiu investigar, na Internet, mais sobre este número e encontrou a seguinte
construção.
[AB] e [FD] são diâmetros da circunferência
de centro O;
CE é tangente à circunferência no ponto D,
logo CE⊥FD;
AE // FD;
FD=CD=1
5.1. Mostra que o comprimento do segmento de recta [AC] é igual ao número de ouro.
5.2. Mostra que os triângulos [AEC] e [ODC] são semelhantes.
5.3. Qual é (aproximadamente) a razão de semelhança que transforma o triângulo [ODC] no
triângulo [AEC]?
5.4. Qual dos quatro números que se seguem é a melhor aproximação do número de ouro
(aproximado às décimas).
(A)
33
400
 31 
(C)  
 51 
15
(B) 2
3
−1
 16 
(D)  
 10 
0
6. Observa a seguinte sequência de figuras:
Na terceira figuras há sete quadrados sombreados, na quarta há 10 quadrados sombreados e na
quinta há 13 quadrados sombreados.
6.1. Quantos quadrados sombreados há na 20ª figura? Explica como chegaste à tua resposta.
6.2. De entre as expressões que se seguem qual a que permite calcular o número de quadrados
sombreados da figura de ordem n?
(A) 3n + 2
(B) 3n - 2
(C) n + 3
(D) 3n
BOM TRABALHO.
-3-
http://hammermat.no.sapo.pt
(Folha de Rascunho)
-4-
http://hammermat.no.sapo.pt