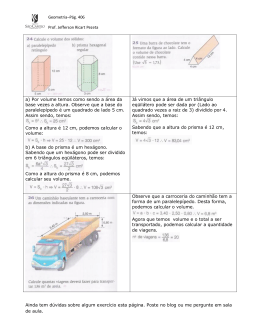
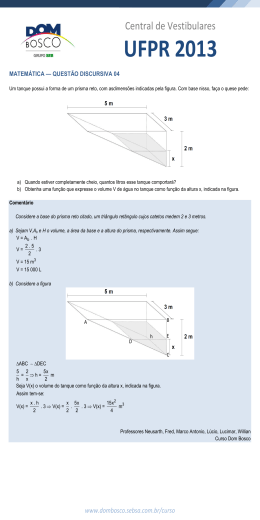
Estudo do Prisma:
Os prismas são poliedros convexos que tem duas faces paralelas e congruentes
(chamadas bases) e as demais faces em forma de paralelogramos (chamadas faces laterais)
Assim temos:
Prisma triangular (as bases são triângulos)
Prisma hexagonal (as bases são hexágonos)
Num prisma, destacamos:



As arestas das bases: AB, BC, CD, DA, EF, FG, GH, HE
As arestas laterais: AE, BF, CG, DH.
Altura do prisma: que é a distância entre os plano que contém as bases.
Quando as arestas laterais são perpendiculares aos planos das bases, o prisma se diz
reto; neste caso, as faces laterais são retângulos congruentes.
Convém notar que, num prisma reto, as arestas laterais tem a mesma medida da altura
do prisma.
Prisma reto (hexagonal)
Um prisma será regular quando for reto e sua base for um polígono regular.
Prisma regular (pentagonal)
No caso de as arestas laterais serem obliquas aos planos das bases, o prisma se diz
oblíquo.
Quanto a base, os prismas comuns estão mostrados na tabela abaixo
Prisma
triangular
Base:
Triângulo
Prisma
quadrangular
Prisma
pentagonal
Prisma
hexagonal
Base: Quadrado Base: Pentágono Base: Hexágono
Área da Superfície de um Prisma
Vamos considerar:



Área da Base(Sb) – é a área de uma das regiões poligonais da base.
Área Lateral (Sl) - a área lateral de um prisma é a soma das áreas de todas as faces
laterais.
Área Total(St) – a área total de um prisma é a soma das áreas de todas as faces do
prisma.
Observe os exemplos.
1° Exemplo: Dado um prisma reto de base hexagonal (hexágono regular), cuja altura é h =
m e cujo raio do círculo que circunscreve a base é R = 2m, calcular :
Planificando o prisma, temos:
a) Cálculo da Area da Base(Sb)
A base é um hexágono regular que pode ser decomposto em 6 triângulos equiláteros, de
lado igual ao raio da circunferência.
Striângulo =
Sb= 6 . S = 6
=
m2
=
m2
b)calculo da área lateral(Sl)
Num prisma regular, sabemos que as faces laterais são retângulos.
Sretângulo = 2 x
m2
Como são 6 retângulos , temos que :
b) Cálculo da área total( St)
2° Exemplo: Num prisma regular, a medida da aresta da base é igual à medida h da altura
do prisma. Sabendo que a área lateral é 10 m2, calcular a área total do prisma.
Resolução: Planificando o prisma temos que:

A face lateral é um retângulo de dimensões a e h.

A base é um triângulo equilátero cujo lado mede a.

Cálculo da área total.