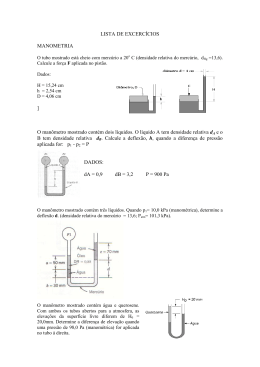
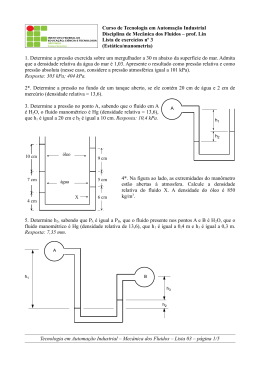
Fenômenos de Transporte I
Centro de Tecnologia – UFAL
Prof. Carlos Ruberto Fragoso Júnior
Lista de Exercícios:
Estática de Fluidos
Nota: Alguns dados não são fornecidos, mas podem ser encontrados na bibliografia especializada.
Alguns problemas numéricos não têm resposta. Consulte o docente se tem dúvidas sobre o
procedimento adotado para resolvê-los.
1. Transformar as seguintes alturas de pressão para pressão em Pascais:
a) 12 mca;
b) 250 mmHg;
c) –250 mmHg.
2. Transformar as seguintes pressões relativas para alturas de pressão em mmHg e mca:
a) 27 psi;
b) 3 atm;
c) –35700 Pa.
3. Explique o princípio de funcionamento do Barômetro de Torricelli.
4. No recipiente da figura 1, a densidade do líquido A é dA = 5. Calcule a densidade do líquido B, dB.
5. Através do convergente da figura 2 flui água. Determina a altura manométrica h, sabendo que a
pressão em A é de 35 kPa.
6. O manômetro em U de mercúrio da fig. 3 mede a pressão de água em A. Se o peso específico do
Hg é 13,6 vezes maior que o da água e a pressão atmosférica é de 765 mmHg, qual é a pressão
absoluta em A quando h1 = 15 cm e h2 = 30 cm ?
7. Uma força P de 850 N é aplicada ao cilindro menor de um macaco hidráulico (Fig. 4). A área a do
2
2
pistão menor é de 15 cm e a área A do pistão maior é de 150 cm . O fluido do pistão é água.
Que carga W deve ser colocada no pistão maior se: a) os pistões estão ao mesmo nível; b) o
pistão maior está 75 cm abaixo do pequeno. Compare os resultados obtidos se o fluido do pistão
fosse trocado por um óleo de densidade d = 0,833.
Resposta:
a) W = 8500 N; b) W = 8610 N.
8. La parte superior de un manômetro de tubo en U invertido está cheio com óleo e o resto do tubo
com água (Fig. 5). Encontre a diferença de pressões (em Pa) entre os pontos A e B (a igual
nível), quando a diferença no nível de água h é de 75 cm.
Dados: dóleo = 0,98; dH2O = 1,01.
Resposta:
pA - pB = -220,07 Pa.
9. Na figura 6 o fluido A é água e o B é óleo (d = 0,9). Se h = 69 cm e z = 23 cm, qual é a diferença
de pressão entre M e N, em kPa?
Resposta:
-1,58 kPa
10. Determine a pressão relativa no ponto P (fig. 7), sabendo que o líquido A tem densidade dA = 0,75
e que a do líquido B é de dB = 1,20. O líquido nas vizinhanças de P é água e o reservatório da
esquerda está aberto à atmosfera.
A
água
60 cm
A
h1
h2
h
Figura 1
Figura 2
Figura 3
Figura 4
Figura 5
Figura 6
Figura 7
11. O Departamento Financeiro de determinada companhia está comprando um sofisticado
equipamento “laser” de $50.000, para medir a diferença de níveis de água entre dois grandes
reservatórios. É importante que pequenas diferenças de nível sejam medidas acuradamente.
Você sugere que a tarefa deve ser desempenhada através da instalação de um manômetro de
$200. Um óleo menos denso que a água deverá ser utilizado para proporcionar uma deflexão no
manômetro 10 vezes maior que a variação de nível entre os dois reservatórios. Assim, uma
pequena diferença de nível entre os reservatórios será aumentada 10 vezes no manômetro.
Determine a densidade do óleo.
Resposta: d = 0,9
12. Para as condições mostradas na Figura 8, determine a força F necessária para levantar o bloco
de concreto (dconcreto = 2,4, diâmetro D = 2 ft, espessura e = 1 ft).
13. Disserte sobre as escalas de pressão e sobre os dispositivos de medição. Em função disto,
resolva o seguinte problema: "Um barômetro é feito com um líquido pesado (símbolo Zz) ainda
não descoberto, de densidade d = 15. Quando o barômetro acusa 702 mm Zz, qual será a
pressão correspondente a um vácuo de 305 mm Zz? Quais são os valores de pressão absoluta e
relativa para este vácuo?"
14. A variação do peso específico de um lodo pode ser expressada pela equação γ = 65 + 0,2 h (γ em
3
lbf /ft e h = profundidade, em ft). Determine:
a- as unidades das constantes "65" e "0,2".
b- o peso específico, massa específica e densidade a uma profundidade h = 15 ft.
c- a pressão relativa e absoluta à mesma profundidade.
Expresse os resultados no Sistema Internacional de unidades.
15. Um brincalhão adicionou óleo, de densidade do, no ramo esquerdo do manômetro da Figura 9.
Não obstante, o manômetro em U ainda é útil como dispositivo de medida de pressão. Ele é
ligado a um tanque pressurizado, como mostra a figura 9.
15.a- Encontre uma expressão para h como função de H e os outros parâmetros do problema.
15.b- Encontre o caso especial de seu resultado em (15.a) quando pres = pa
15.c- Admita que H = 5,0 cm, pa é 101,2 kPa, pres é 1,82 kPa mais alta que pa e do = 0,85.
Calcule h em cm, ignorando os efeitos da tensão superficial e desprezando os efeitos da
densidade do ar.
F
pa
água doce
Reservatório
pressurizado de
ar, com
pressão = pres
5 ft
11 ft
Óleo
H
h
água salgada (d = 1,027)
Figura 9
Água
Figura 8
1m
16. O tanque da figura 10 está pressurizado,
como mostra a leitura do manômetro de
mercúrio. Determine a força hidrostática
por unidade de largura sobre a comporta
AB.
0,8 m
Hg
água
5m
Figura 10
A
2m
B
3
17. Em um reator químico de 200 ft de altura, a massa específica de um fluido, em slug/ft , varia com
a distância z (em ft, medida desde o fundo do reator) segundo a relação:
2

z
 z  .
ρ = 0,020 1 −
+
 
 500  1000  
Supondo que o fluido está em repouso, determine:
17.a a diferença de pressões entre o fundo, pf, e a superfície, ps , do reator;
17.b as unidades das constantes « 0,020 », « 500 » e « 1000 »;
17.c a diferença de pressões entre o fundo, pf, e a superfície, ps, do reator.
Expresse os resultados no Sistema Internacional.
Empuxo
18. Uma pedra pesa 540 N no ar e 240 N quando submersa em água. Calcular o volume, a massa
específica e a densidade da pedra.
3
Rta.: v = 0,03 m ; d = 1,84.
19. Um objeto prismático, de 20cm × 20cm × 40 cm, é pesado na água a 50 cm de profundidade,
dando 50 N. Quanto pesa no ar e qual é a sua densidade?
Rta.: d = 1,3.
20. Um densímetro pesa 0,0022 N e seu extremo superior é um cilindro de 0,28 cm de diâmetro. Qual
será a diferença entre os comprimentos da parte do cilindro emergente, quando o densímetro flutua
em óleo de densidade 0,78 e álcool de densidade d = 0,821? Nota: pesquise o que é um densímetro,
para resolver este problema.
Rta.: h = 2,28 cm.
21. Um bloco prismático de madeira flutua na água, sobressaindo da superfície 5 cm. Quando é
colocado em glicerina (d = 1,35), sobressaem 7,5 cm da superfície do líquido. Determinar a
densidade do bloco de madeira.
Rta.: d = 0,66.
22. A que profundidade afundará um tronco de 2,4 m de diâmetro e 4,5 m de comprimento, em água
doce, se a densidade da madeira é d = 0,425?
Rta.: .h = 1,06 m.
3
23. Uma esfera de 120 cm de diâmetro flutua em água salgada (ρ = 1025 kg/m ), a metade dela
3
submersa. Que peso mínimo de concreto (ρ = 2400 kg/m ), utilizado como âncora, será necessário
para submergir completamente a esfera?
Rta.: 8100 N.