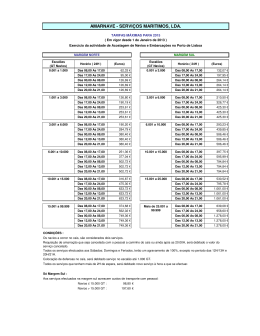
Disciplina: Pesquisa Operacional
Curso: Especialização em Métodos Quantitativos:
Estatística e Matemática Aplicadas
01. O número de falhas por dia em uma fábrica segue uma Poisson com parâmetro λ = 3. A empresa tem
recursos internos que lhe permitem reparar até três máquinas por dia. Quando as falhas ultrapassam
três em um só dia, é contratada assistência externa para executar os consertos excedentes.
01.1. Qual a probabilidade de que, em um dado dia, se tenha que requisitar assistência externa?
01.2. Qual o número esperado de consertos diários realizados pela empresa?
01.3. Qual o número esperado de consertos diários realizados pela assistência externa?
01.4. Qual a probabilidade de que, em um determinado dia, seja necessário enviar mais do que duas
máquinas para conserto externo.
02. O número de navios petroleiros que chegam à determinada refinaria por dia tem uma distribuição de
Poisson de parâmetro três. As instalações atuais do porto podem atender, no máximo, quatro navios
por dia. Os eventuais excedentes deverão seguir para outro porto.
02.1. Num dia, qual a probabilidade de haver navios que não possam ser atendidos?
02.2. Qual o número esperado de navios que são atendidos diariamente na refinaria?
02.3. Qual o número esperado de navios que terão de se dirigir diariamente a outro porto?
02.4. De quanto deverão ser aumentadas às instalações atuais para permitir atender todos os navios
em aproximadamente 99,5% dos dias de serviço?
03. Suponha que a duração de uma chamada de celular (em minutos) é exponencialmente distribuída com
parâmetro de 0,4. Determine:
03.1. O tempo médio e a variabilidade da duração das chamadas.
03.2. A probabilidade de que uma chamada dure entre 2 e 5 minutos.
03.3. A mediana, o primeiro, o terceiro e a amplitude interquartílica do tempo de chamada.
03.4. A probabilidade de que a duração supere o valor esperado.
04. O tempo de espera, numa parada, pela chegada de um ônibus é, em média, de 5 minutos. Admitindo que
esse tempo é uma variável exponencial, determine a probabilidade de que alguém:
04.1. Espere mais de 15 minutos por ônibus.
04.2. Espere mais de 15 minutos por ônibus. Resolva utilizando a Poisson.
04.3. Pegue um ônibus no minuto imediatamente seguinte à chegada na parada.
04.4. Espere por mais de 10 minutos por um ônibus dado que já esperou 15 minutos.
Prof. Lorí Viali, Dr.
-
[email protected]
-
http://www.pucrs.br/famat/viali/