Aplicação das Redes Neurais
Artificiais na Confiabilidade
Metrológica
Centro Técnico Aeroespacial – CTA
Universidade de São Paulo - USP
A estrutura da apresentação
METROLOGIA
FOCALIZAÇÃO
Uma parte da metrologia
RRBF´s
Laboratórios de Calibração
Uma parte das Redes Neurais
Artificiais
Laboratórios de Ensaio
MLP´s
Controle dos PC´s
REDES NEURAIS ARTIFICIAIS
Ajuste das CC´s
R
E
S
U
L
T
A
D
O
S
A estrutura da apresentação
METROLOGIA
Uma parte da metrologia
ACREDITAÇÃO NA MEDIÇÃO
Acreditação na medição
CONFIABILIDADE
METROLÓGICA
CALIBRAÇÃO
INSTRUMENTO
.....
...........
EVOLUÇÃO ATRAVÉS DO TEMPO
A confiabilidade metrológica
Rastreabilidade
Manuseio e
Armazenamento
Métodos
Equipamentos
Amostragem
Condições
Ambientais
Pessoal
A estrutura da apresentação
METROLOGIA
Uma parte da metrologia
Uma parte das Redes Neurais
Artificiais
REDES NEURAIS ARTIFICIAIS
O neurônio artificial
x
w
∑
vj
bj
1
α
yj
yj = α(wT x + bj)
x = vetor de entrada
bj = valor de limiar
w = vetor pesos
vj = campo indutivo
α = função de transferência
yj = saída do neurônio
A função de transferência α
vj
α
yj = { 2 / [1+exp(-2 vj)] } – 1
yj
y j = C vj
O neurônio das RRBF´s
vj
α
yj
vj = x - w
yj = exp – ( b || vj ||2)
yj = exp – [ (0,8326/LFB) || vj ||2]
As arquiteturas das RNA´s
RRBF´s
MLP´s
x1
x1
F1(x)
x2
F2(x)
xm
Fk(x)
F1(x)
x2
Fk(x)
xm
RRBF´s Fk (x) = Σ j=1:N w2jk exp –[||w1j-x||2 (0,8326/LFB)]
MLP´s Fk (x) = αk [Σj=1:N w2jk [αj (Σ m=1:Nx w1jmxm)]]
w1- primeira camada
w2 – segunda camada
N – Nº neurônios da primeira camada
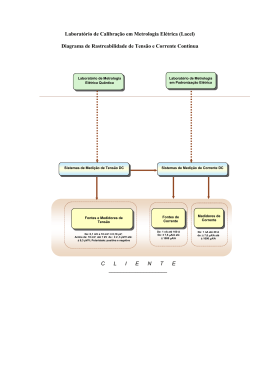
Lab. Calibração x Lab. Ensaios
Calibração
Ensaios
Poucos pontos medidos
(~ uma dezena)
Quantidades apreciáveis de medições
Medições unidimensionais
Medições em diversos pontos em
diversas grandezas
Ambiente confinado com condições
ambientais controladas
Nem sempre é possível confinar o
ambiente e controlar as condições
ambientais
Busca-se condições físicas ideias
Testes em condições ideais e em
condições adversas
CC´s identidade ou lineares
As relações entre as grandezas e os
pontos de medição freqüentemente
carregam relações não lineares.
RNA escolhida RRBF
RNA escolhida MLP
A estrutura da apresentação
METROLOGIA
FOCALIZAÇÃO
Uma parte da metrologia
RRBF´s
Laboratórios de Calibração
Uma parte das Redes Neurais
Artificiais
Controle dos PC´s
REDES NEURAIS ARTIFICIAIS
Ajuste das CC´s
R
E
S
U
L
T
A
D
O
S
A aplicação das RRBF´s I
Laboratórios de Calibração
• São três parâmetros a serem ajustados na RRBF:
• Os centros das funções de Base
• Escolhendo-se os centros das funções de base coincidentes com
os valores de entrada conseguimos uma FP nula (EQM=0).
ε = ∑ j∈C ej2
ou εav = (1/Z) ∑j∈C ej2
Sendo C sendo conjunto de neurônios da camada de saída e Z o número de medições.
•
Os pesos sinápticos w da camada linear
• Calculados para garantir que a curva aproximada reproduza
fielmente os pontos medidos. (garantia de EQM nulo).
A aplicação das RRBF´s I
Laboratórios de Calibração
• As larguras dos centros das funções de Base
• São responsáveis, neste tipo de aproximação, pela interpolação
(embora os pesos sinápticos tenham influência).
Medindo a qualidade da interpolação
• Para medir a qualidade da interpolação foram propostos neste
trabalho, dois indicadores baseados nas FR´s:
• AMQ = (1 / 2N) Σ n=1:N Σj ej2 = (1 / 2N) Σ n=1:N Σj (f(x)-F(x))2
Sendo F(x) a função aproximada N o Nº pontos considerados
• AM = (1 / 2N) Σ n=1:N Σj ej = (1 / 2N) Σ n=1:N Σj (f(x)-F(x))
• Td = 2AM (levando em conta a interpolação)
Experimentos computacionais.
Pontos eqüidistantes e não eqüidistantes.
AMQ
AMQ
Referência [17,Haykin] LFB => d/2
Referência [13, Hertz] LFB => 1.1775dmax/sqrt (2.nº neurônios ocultos).
O desfecho para estes ensaios computacionais
•Para b = 0.8326/LFB a aproximação pela RRBF será:
yai (xi) =
Σm= 1:N exp –(|xi-xcm|2 .b) . {dm - [Σ n= 1 n≠m : N wn . exp –(|xcm-xcn|2 .b)]}
lim (b→0) [exp (x-z)2 .b] – [(x-z).b +1] = exp (0) – [ 0 +1] = 1 –1 = 0
exp (x-z)2.b ≅ (x-z).b +1
então:
no limite em que b→0
yai (xi) =
Σm= 1:N –[(|xi- xcm|2 .b)+1] . {dm -[Σ n= 1 n≠m:N wn .–[(| xcm- xcn |2 .b)+1]}
(uma combinação linear dos valores de entrada)
Para LFB ≠ ∞ pois, do contrário, Σ n= 1 (n≠m):N wn = dm ∀ dm
Aplicando as RRBFs nos Lab. Calibração
• O critério de parada
• - Um Valor Quadrático Médio de Afastamento que não
ultrapassasse do valor médio entre pontos medidos e a função
de referência, e
VQMA (n) = sqrt ((AMQ .2) / Z)
- Valores de AMQ e AM que não variassem mais do que 0,1E-6
em duas iterações consecutivas.
AMQ
Lab. Calibração – Grandezas iguais I
Valor
Indic.
nominal
Padrão
(psi)
(psi)
(psi)
12,0
24,0
36,0
48,0
60,0
72,0
84,0
96,0
108,0
120,0
10,448
23,972
35,802
47,637
59,466
71,297
83,132
94,969
106,803
118,637
10,5
23,9
35,8
47,9
59,8
71,6
83,3
95,1
107,2
119,0
Passo
LFB
0,50
1ºCarr. 2ºCarr.
1ºDesc.
Análise dos
erros2ºDesc.
sistemáticos
Azul – 1º Carr.
Verm. – 2º Carr.
Verde – 1º Descarr.
AMQ
0,032
Mag. – 2º Descarr.
acidentais:
(psi)
(psi)
e
(psi)
10,5
11,0
10,5
Alterando
o
valor
60.0
para 61.0 - 2º
23,9
24,0
24,0
35,8
36,0
35,9
descarregamento
(diferença
de 1.66%)
47,9
59,9
71,8
83,6
95,4
107,3
119,0
48,0
60,1
72,0
83,9
95,7
107,4
119,0
48,0
60,1
72,0
83,9
95,7
107,4
119,0
LFB de 220.5 => 248.5 (11.46%)
AMQ de 0.1733 => 0.2384 (35.49%).
0,070
0,142
0,1373
Validação
dos ciclos:
0,24-0.7344
0,229
Dmáx
(0.07344%)
AM
0,091
0,146
LFB
253
255,5
248,50
Classe232,5
A4 (ISO14105)
±0.1%
Obs: Fundo de escala 1000psi
Processo de Calibração CP16 do manômetro analógico de ponteiro
marca Wallace & Tiernan com padrão do tipo peso morto (RUSKA).
Lab. Calibração – Grandezas iguais II
Determinação dos pontos aCarregamento
serem medidos Descarregamento
no PC:
Valor do padrão
Pressão Padrão
Indic. Objeto
Pressão Padrão
Indic. Objeto
911,00
909,412
909,66
909,413
909,64
Valores de AM constante.
Valores
de AMQ
variam
(hPa)
(hPa)
(hPa) 0.01.
(hPa)
(hPa)
850,00
848,43 em verificações.
848,149
848,41
6 pontos são suficientes
para o848,154
PC , 3 pontos
1030,00
1028,992
1029,21
1028,992
Processo de Determinação
da
histerese:
0,029
AMQ
AMQ
03 pontos
Calibração CP06 AMQ Passo LFB AM AM Indicação
-0,121sugerida
AM
Possivelmente
90,53
11588 não há LFB
LFB
Diferenças
não
com
pontos
X
X
histerese no contexto
945,00
consideráveis
944,416
944,65
944,415
estatístico
escalonados do X 877,00
874,405
874,67
874,400
Pode
ser
calculada
uma
979,00
976,485
976,70
976,487
barômetro
histerese
ou
uma
pseudo0,028
AMQ
AMQ
06 pontos
X
Diferenças
histerese
Passo LFB
-0,119
AM
AM
microprocessado
consideráveis
Pode
ser
calculada
e
4,52
605,61
LFB
LFB
X
atribuída uma histerese à
ADT com padrão X 860,00
859,820
860,06
859,815
calibração
894,00
do tipo peso morto
891,910
892,17
891,909
928,00
926,913
927,16
926,914
(RUSKA).
962,00PC,
961,911 Hint= 962,14
961,910
•Calculando a histerese deste
| Tdc – Tdd
| = 0.02
1013,00
Diferenças AM => 0.11
11 pontos
Passo LFB
2,26
1011,489
AMQ
1029,21
0,026
-0.113
11859
944,62
874,63
976,69
0,023
-0,108
597,50
860,06
892,16
927,14
962,13
1011,71
0,028
1011,489
AMQ
1011,70
0,025
171,74
LFB
171,76
Diferenças-0,119
entre AMQ
=> 0.005
-0,111
AM
AM
LFB
Uma pseudo – histerese pode ser calculada.
Resultados Obtidos
•
Validação dos ciclos de calibração
•
Análise dos erros sistemáticos e acidentais
•
Determinação dos pontos a serem medidos no PC
•
Determinação da histerese
•
Os erros sistemáticos => Td = 2AM
•
Validação dos pontos medidos no PC
•
Aproximação da CC para grandezas diferentes e não lineares
(exemplo termopares)
•
Aproximação da CC com EQM ≠ 0 com a máxima probabilidade
do qui quadrado
•
Resultado para RRBF – Escolha respaldada da LFB
A estrutura da apresentação
METROLOGIA
FOCALIZAÇÃO
Uma parte da metrologia
RRBF´s
Laboratórios de Calibração
Uma parte das Redes Neurais
Artificiais
Laboratórios de Ensaio
MLP´s
Controle dos PC´s
REDES NEURAIS ARTIFICIAIS
Ajuste das CC´s
R
E
S
U
L
T
A
D
O
S
A balanças externa do túnel de vento
F4
F5
F6
F2
F1
Símbolo
Denom.
Português
Símbolo
medição
D
Arrasto
F1
Y
Lateral
F2
L
Sustentação
F3
rol
Rolamento
F4
arf
Arfagem
F5
gui
Guinada
F6
CA
Centro Aer.
-
F3
O método de calibração:
a Cruzeta com Pesos Suspensos
O método de aprendizado.
O desenvolvimento para correção do erro.
•O vetor de erros e pode ser linearizado se considerarmos ∆w
pequena e se a função erro em relação aos pesos não possuir
grandes não linearidades:
e (n,w) ~ e (n) + JT (n) (w(n+1)-w(n))
•Substituindo na equação de performance, para C sendo
conjunto de neurônios da camada de saída:
ε (n) = Σj∈C
ej2 (n)
•Derivando a ultima equação e igualando a zero chegamos à
regra de aprendizado:
-1 JT-1
(n)J(n)+µI)
(n)
(n) e(n)
JTe(n)
w (n+1) = w(n) – (JT(n)J(n))
O método de Levenberg – Maquardt nas
MLP´s . Mais dificuldades:
Dificuldade
Causa
Solução adotada
Não aceitação pelo Admitir variação
O incremento dos
da FP em 100
algorítimo do
valores de µ podem
ultrapassar a
incremento da função ppm´s para mais
capacidade da
de performance
máquina
A inicialização tem Saturações precoces Valores iniciais
dos pesos
das funções de
efeito na FP da
próximos de zero
transferência dos
aproximação
neurônios
30.0
26.769
A aproximação da CC utilizando a
MLP de duas camadas
Somatória quadrática = FP =
25.0
ε=Σ
j∈C
ej2
0.725
0.830
0.800
0.396
0.378
0.275
0.337
0.281
0.351
0.278
0.209
20
21
22
23
24
25
26
27
28
29
30
1.491
1.641
17
3.011
1.998
3.556
15
Somatória quadrática do polinômio = 1,63
16
3.937
5.0
14
5.469
5.398
10.0
6.356
10.854
15.0
500 ciclos de treinamento
8.707
20.0
17.963
17.699
19
13
12
11
10
9
8
7
6
0.0
18
Somatória quadrática
Abaixo de 6 neurônios ocultos FP ~ 104 a 105
Número de neurônios da camada oculta
100
6
7
8
9
Número de neurônios na camada oculta
120.74
101.41
106.32
127.69
116.33
123.17
126.81
115.66
105.99
168.64
173.34
220.29
204.98
188.03
197.13
206.41
183.75
173.77
180.33
184.51
157.51
163.09
Prédição apêndice II
109.78
117.70
98.96
112.65
174.80
159.53
99.07
119.06
161.65
152.09
105.30
99.50
165.71
157.33
108.31
110.51
157.63
163.91
108.40
116.02
124.48
216.34
198.77
186.56
200
159.45
140.84
150
178.22
250
167.93
Soamatória quadrática
A capacidade de predição em um mês
Prédição apêndice III
50
Um erro em módulo constante e igual a 0.71 => FP = 220.80
500 ciclos de treinamento
0
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
A consideração das incertezas no
aprendizado I
•Alterando a equação de performance, para C sendo conjunto de
neurônios da camada de saída e uj2 a matriz diagonal das variâncias:
ε (n) = Σj∈C
(ej / uj)2 (n)
•Linearizando o vetor de erros e, substituindo na função de performance
acima, derivando esta última e igualando-a a zero obtemos a regra de
aprendizado considerando as incertezas:
w (n+1) = w(n) – (JT(n) (uj2)-1 J(n)+µI)-1 JT(n) (uj2)-1 e(n)
•O que é equivalente a substituir os elementos J da Jacobiana J pelos
elementos Jinc e os elementos do vetor e pelos elementos einc :
Jinc(j,n+i) = J(j,n+i) / un
para linha j e coluna i un associada a Fn
eincj = ej/un
50
100
0
6
7
8
9
106.46
3.84
107.19
Número de neurônios na camada oculta
154.94
97.19
109.09
109.56
109.95
0.66
0.49
0.59
0.52
94.56
158.34
2.12 101.03
153.86
175.31
177.42
180.84
Prédição apêndice III
0.51
155.07
95.28
1.70
154.72
95.65
1.27
154.95
95.81
145.64
156.21
147.28
154.47
1.41
2.38 93.12
3.23
2.33 100.11
107.33
3.72
154.52
157.09
308.5
306.5
Prédição apêndice II
114.01
4.97
164.33
145.99
235.86
274.84
205.96
167.41
163.35
153.19
112.38
6.50
165.17
7.52 107.22
110.82
119.66
7.75
5.49
115.40
7.49
14.70
205.24
150
34.41
56.93
250
267.51
251.06
350
54.59
200
217.40
300
42.72
Soamatória quadrática
A consideração das incertezas no
aprendizado II
Treinamento apêndice I
500 ciclos de treinamento
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
O perfil das incertezas e o perfil das FP´s
considerando ou não as incertezas
0.40
0.35
0.30
0.25
0.20
0.15
0.10
0.05
MLP com 30 neurônios ocultos
0.00
F1
F2
F3
F4
F5
F6
Incertezas estimadas
0.04172
0.04087
0.11814
0.03005
0.03938
0.36916
FP da rede / incertezas iguais a unidade
0.05608
0.06784
0.04048
0.01352
0.02575
0.04137
FP da rede / incertezas estimadas
0.00446
0.05558
0.25303
0.00245
0.01156
0.18137
Os resultados obtidos
As contribuições para a metrologia
• O confinamento na aproximação da Curva de Calibração.
• As predições como indicador de repetitividade.
• A determinação do intervalo de calibração.
As contribuições para as MLP´s
• A consideração das incertezas nas MLP´s.
Itamar Magno Barbosa
[email protected]
[email protected]