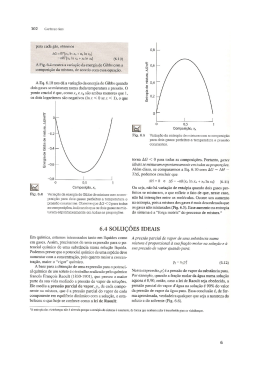
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
28 de junho a 1º de julho de 2004 – Curitiba-PR
1
MINIMIZAÇÃO DE CUSTOS EM MISTURAS CERÂMICAS CIMENTANTES
J. V. Nardi (1), (3), D. Hotza (2), (3)
Rua Lauro Bustamante 36, Itaguaçu, 88085-590Florianópolis – SC
[email protected]
(1)
Centro Federal de Educação Tecnológica (CEFET/SC)
(2)
Departamento de Engenharia Química da UFSC
(3)
Programa de Pós-Graduação em Ciência e Engenharia de Materiais da UFSC
RESUMO
O trabalho tem como finalidade demonstrar a possibilidade de minimizar custos,
na produção de materiais cerâmicos, através da análise de superfície de resposta. O
estudo em fase preliminar é desenvolvido em mistura composta por três
componentes que, reagindo entre si, origina um produto final com propriedade
cimentante. Utilizam-se procedimentos da teoria de projetos de misturas que,
através de ensaios laboratoriais, da representação gráfica triangular e de um valor
máximo pré-estabelecido para a resistência do produto, determinarão as proporções
dos componentes que irão minimizar o custo final do material em questão.
Palavras-chave: Minimização de custos, materiais cerâmicos, cimentação.
INTRODUÇÃO
A teoria de planejamento e otimização de experimentos permite o
conhecimento, através dos valores esperados, da variação do comportamento das
propriedades mecânicas de produtos, quando formados através de misturas entre
diversos componentes. Como é de conhecimento, diferentes proporções entre os
mesmos componentes podem manter constante uma determinada propriedade a ser
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
2
28 de junho a 1º de julho de 2004 – Curitiba-PR
estudada
(1)
. Levando este caso para a produção industrial, concluímos que: é
possível minimizar o custo de um produto em função de correlações existentes entre
a variação de suas percentagens na mistura, mantendo o mesmo padrão de
qualidade do produto final em questão.
Deseja-se
desenvolver
um
material
cimentante
constituído
por
três
componentes (x1, x2 e x3) e que após reação de hidratação desenvolva uma
resistência esperada à compressão, em torno, de 3.000 kPa. As condições de
projeto impõem à determinação das percentagens dos componentes que minimizem
o custo por tonelada do produto final, através da adaptação de um modelo
quadrático com, no mínimo, um coeficiente de correlação (r2) igual a 0,90.
MATERIAIS E MÉTODOS
Na Tabela I é mostrada a análise química dos materiais pulverulentos (x1 e x2)
utilizados. O primeiro constituído por um rejeito industrial e o segundo por uma cal
hidratada comercial.
Tabela I Análise química dos materiais pulverulentos sólidos utilizados.
ÓXIDOS
COMPONENTE 1 (x1, %)
COMPONENTE 2 (x2, %)
SiO2
53,60
0,3
Fe2O3
8,33
-
Al2O3
28,60
71,40
CaO
1,35
-
MgO
0,91
-
Na2O
1,10
-
K2O
2,32
-
SO3
0,82
-
Perda ao fogo
4,01
28,20
insolúvel
0,39
-
O terceiro componente é constituído pela água (x3), que atua nas reações de
hidratação para a obtenção do produto final cimentante.
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
3
28 de junho a 1º de julho de 2004 – Curitiba-PR
A teoria matemática sobre planejamento e otimização de experimentos
encontra-se
em
literatura
especializada
(2),
(3),
(4)
.
A
relação
entre
os
pseudocomponentes e os componentes originais é dada pelas expressões em (A).
x'i =
( xi − Li )
1− L
(A)
3
L = ∑ Li < 1
i =1
Sendo:
x'i Æ pseudocomponentes;
xi Æ componentes originais;
Li Æ limite inferior; e
i Æ componentes (i = 1, 2, 3).
Para este caso o estudo é desenvolvido através de modelo quadrático, dado
pela expressão matemática em (B).
Re = b1x'1 + b2x'2 + b3 x'3 + b12x'1x'2 + b13x'1x'3 + b23x'2x'3
(B)
sendo:
Re Æ Resistência esperada à compressão;
x'1 Æ % do componente 1;
x'2 Æ % do componente 2;
x'3 Æ % do componente 3; e
b1, b2, b3, b12, b13, e b23 Æ coeficientes da equação adaptada.
O coeficiente de correlação (r2) é obtido através da Equação em (C).
9
r2 =
∑ (R
− R )2
∑ (R
− R)
i =1
9
i =1
sendo:
ei
i
(C)
2
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
4
28 de junho a 1º de julho de 2004 – Curitiba-PR
ReiÆ Resistências esperadas (resultados do modelo quadrático);
R Æ Média de todas as resistências observadas (laboratório);
Ri Æ Resistências observadas (laboratório); e
i
Æ 1, 2, .....,9 (no de ensaios laboratoriais).
Na confecção dos corpos de prova, inicialmente, a mistura foi trabalhada a seco
e em seguida, mecanicamente, numa misturadora a baixa velocidade durante 5
minutos. Após a adição de água, para a obtenção da umidade desejada, o mistura
prosseguiu por mais 5 minutos. A moldagem dos corpos de prova, com 20cm de
altura por 10 cm de diâmetro, foi efetuada através de compactação mecânica, em
cilindros de paredes laterais tripartidas, com uma energia de compactação de
1.320,84 kPa. Os corpos de prova foram ensacados para evitar a carbonatação
devido ao dióxido de carbono do ar e mantidos por um período de 28 dias de cura.
Cada ponto representa a média de três corpos de prova, com tensões calculadas em
kPa e variação de ± 10% em torno da média. O planejamento experimental inicial
envolve misturas onde as proporções dos materiais variam de 7,93% a 38,91% para
a primeira componente (x1), 38,06% a 67,57% para a segunda (x2) e 15,09% a
40,54% para a terceira (x3). O planejamento inicial envolve 9 casos (27 corpos de
prova) e a pesagem dos materiais, em laboratório, foi efetuada com precisão do
centésimo da grama. Na Tabela II é visualizado o planejamento experimental
desenvolvido através dos 9 casos testados em laboratório.
Tabela II Planejamento experimental.
CASOS
x1 (%)
x2 (%)
x3 (%)
x'1
x'2
x'3
R (kPa)
1
25,65
41,70
32,65
0,33193
0,0
0,66807
2510
2
31,68
51,51
16,81
0,58625
0,41375
0,0
2260
3
17,78
46,23
35,99
0,0
0,19106
0,80894
2304
4
22,45
58,37
19,18
0,19696
0,70308
0,09996
2143
5
21,715
43,935
34,32
0,16596
0,09426
0,73851
3400
6
28,665
46,605
24,73
0,45909
0,20877
0,62048
2650
7
27,065
54,94
17,995
0,39161
0,55841
0,04998
3605
8
20,115
52,30
27,585
0,09848
0,44707
0,45445
3300
9
24,39
49,4525
26,1575
0,27879
0,32697
0,39424
3810
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
5
28 de junho a 1º de julho de 2004 – Curitiba-PR
Os valores da tabela anterior são apresentados sob as formas de coordenadas
originais (x1, x2, x3), de pseudocomponentes (x'1, x'2, x'3) obtidos pelas expressões
em (A) e as correspondentes resistências observadas em laboratório (R).
RESULTADOS E DISCUSÃO
Aplicando-se a teoria do método dos mínimos quadrados nos dados da Tabela
II obtemos a Equação (D), que corresponde à adaptação do modelo quadrático em
(B) e que gera o valor da resistência esperada à compressão como uma função das
percentagens dos componentes, expressa sob a forma de pseudocomponentes.
Re= -10897,38x'1 -3911,77x'2+1984,09x'3+41989,17x'1x'2+21253,68x'1x'3 +10469,96x'2x'3 (D)
Para esta equação os cálculos indicam ser o coeficiente de correlação (r2) igual
a 0,93, segundo a Equação (C) . Para valores menores que 0,90 o desenvolvimento
de novo planejamento experimental é necessário, de tal forma que conduza a outra
equação com ajuste mais adequado.
A expressão matemática dada em (D) pode ser representada espacialmente
por um gráfico com base triangular, onde os valores das resistências esperadas são
Resistência (R e , kPa)
plotados ortogonalmente sobre esse triângulo, conforme visualizado na Figura 1.
abaixo de 3000 kPa
3000
above
acima de 3000 kPa
X'3
X'1
X'2
Figura 1 Representação espacial da Equação (D) obtida através do planejamento
experimental, dado pela Tabela II em pseudocomponentes.
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
28 de junho a 1º de julho de 2004 – Curitiba-PR
6
O gráfico espacial é dividido em duas regiões, sendo que no contato entre
ambas estão localizadas todas as proporções, entre os três componentes, que
atendem à condição desejada: uma resistência esperada em torno de 3.000 kPa.
A projeção da superfície espacial sobre a base triangular fornece a Figura 2,
através da representação sob a forma gráfica triangular. Corresponde à superfície
de resposta à adaptação do modelo quadrático, através de curva de nível cujo valor
esperado varia em torno de 3000 kPa, conforme o estipulado nas condições iniciais
de projeto.
X'3
A
0,9
0,1
abaixo de 3000 kPa
3000
above
acima de 3000 kPa
5
0,3
B
a
30,8
0,2
0,7
1
0,6
0,4
0,5
0,5
8
0,6
b
0,4
9
6
0,7
0,3
0,2
0,8
0,9
0,1
4
7
X'1
0,1
0,2
0,3
0,4
2
0,5
0,6
0,7
0,8
0,9
X'2
Figura 2 Representação da superfície de resposta da Equação (D) obtida através do
planejamento experimental, dado pela Tabela II em pseudocomponentes.
A outra condição de projeto se refere à determinação das percentagens dos
componentes, de tal forma que minimizem o custo por tonelada do produto final. São
cotados os custos em R$ 118,00 por tonelada para o componente 1, em R$ 26,00
por tonelada para o componente 2 e em R$ 3,31 por metro cúbico do componente
3. Desejando-se o menor custo, para o produto final, traça-se na Figura 2 uma reta
paralela ao eixo x'2 x'3 e que seja tangente à curva de nível fixada por 3000 kPa
(paralela A interceptando o ponto tangente em a). Os valores x'1 = 0,054, x'2 = 0,246
e x'3 = 0,70 satisfazem as condições. Transformando em coordenadas originais
teremos x1 = 19,06%, x2 = 47,54% e x3 = 33,40%. Para estes valores o custo terá um
valor mínimo de R$ 35,96 por tonelada. Por outro lado, várias são as proporções dos
componentes capazes de produzir um produto final que satisfaça a condição de
resistência em torno de 3000 kPa. Isto nos leva à existência da possibilidade oposta,
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
28 de junho a 1º de julho de 2004 – Curitiba-PR
7
que seria o caso do maior custo (paralela B interceptando o ponto tangente em b).
Os valores de x'1 = 0,513, x'2 = 0,472 e x'3 = 0,015 satisfazem a referida condição.
Transformando em coordenadas originais teremos x1 = 29,94%, x2 = 52,89% e x3 =
17,17%. Para estes valores o custo terá um valor máximo de R$ 49,65 por tonelada.
Como se constata pode-se produzir um produto final, que satisfaça as condições
desejadas, variando de R$ 35,96 a R$ 49,65. A utilização do primeiro caso resultará
em uma redução de R$ 13,69 por tonelada de produto, correspondendo a uma
economia de 27,57% em relação ao mais oneroso.
Este procedimento é válido para o caso em questão e o custo refere-se
somente ao preço dos componentes, não levando em consideração outros fatores
que entram na composição do custo final do produto acabado.
CONCLUSÃO
ÆA superfície de resposta obtida através da adaptação do modelo quadrático
respondeu favoravelmente ao coeficiente de correlação solicitado, isto é: r2 > 0,90;
ÆA equação ajustada, através do método dos mínimos quadrados, permite
representar a propriedade mecânica na forma espacial e/ou superficial. Isso é feito
através da resistência esperada em função da variação das percentagens dos três
componentes formadores do produto em questão;
ÆOs valores obtidos de 19,06% para o componente 1, de 47,54% para o
componente 2 e 33,40% para o componente 3 minimizam o custo final;
ÆA economia na utilização deste artifício é de R$ 13,69 por tonelada,
correspondendo a uma capitalização de 27,57% em relação ao maior custo; e
ÆIndependente de se impor ou não uma série de restrições, sejam elas condições
matemáticas, limites nos intervalos de variação dos componentes, ou na própria
propriedade mecânica do produto à obtenção da característica desejada, conclui-se
ser possível a utilização deste procedimento na minimização do custo final.
REFERÊNCIAS BIBLIOGRÁFICAS
1.
J. V. Nardi, W. Acchar, D. Hotza, Enhancing the Properties of Ceramic Products
Through Mixture Design and Response Surface Analysis, Journal of the
European Ceramic Society, 24 (2004) pp.375-379.
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
28 de junho a 1º de julho de 2004 – Curitiba-PR
2.
J. A.
8
Cornell, How to Run Mixture Experiments for Product Quality, Vol. 5
(American Society for Quality Control, 1990).
3.
A. D. Montgomery, Desing and Analysis of Experiments, 4 ed. (Arizona State
University, 1996).
4.
Statistica, Volume 4, Industrial Statistic, Statsoft, 1995.
Anais do 48º Congresso Brasileiro de Cerâmica
th
Proceedings of the 48 Annual Meeting of the Brazilian Ceramic Society
28 de junho a 1º de julho de 2004 – Curitiba-PR
9
COSTS MINIMIZATION IN CEMENTING CERAMIC MIXTURES
ABSTRACT
This paper is intended to demonstrate the possibility to minimize the production cost
of ceramic materials through the analysis of the response surface. This preliminary
study was developed for a three components-mixture, which after reacting together
creates a final cement propriety product. The procedures are based on laboratorial
tests, triangular graphic representation and pre-established maximum value for the
product strength. Based on the affirmations above, it was possible to determine the
components proportion to decrease the final cost.
Key-words: cost minimization, ceramic materials, cimentation