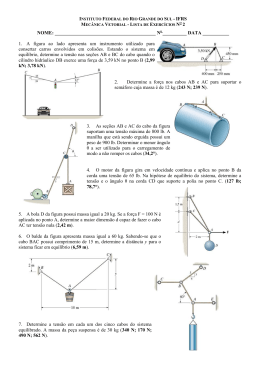
Lista de Exercícios – Aula 02
Vetores, Soma de vetores e Sistema de coordenadas.
1 - No diagrama abaixo, represente:
a)
b)
c)
d)
e)
⃗ =𝑨
⃗⃗ + 𝑩
⃗⃗
𝑪
⃗⃗ = −𝑨
⃗⃗
𝑫
⃗𝑬
⃗ = 𝟐𝑩
⃗⃗
⃗𝑭 = 𝟐𝑨
⃗ − ⃗𝑩
⃗
⃗⃗𝑮 = 𝟑𝑨
⃗ + 𝟎, 𝟓𝑩
⃗⃗
2 - (R. C Hibbeler ) O gancho mostrado na figura abaixo está sujeito a duas
forças F1 = 60N e F2 = 90 N. Determine o
módulo da força resultante, utilizando a lei
dos cossenos.
R  F = 94,36 N
1
3 - (R. C Hibbeler – Mecânica) O elo mostrado na figura abaixo está sujeito a
duas forças F1 e F2. Determine o módulo
da força resultante, utilizando a lei dos
cossenos.
R  F = 685,44 N
4 - Os cabos de sustentação AB e AC estão presos no topo da torre de
transmissão. A força de tração no cabo AC vale 8 kN. Determine a força de tração
T necessária no cabo AB, tal que o efeito resultante das duas forças de tração nos
cabos, seja uma força direcionada para baixo no ponto A. (lei dos senos)
5 - Represente os vetores abaixo em termos dos vetores unitários 𝒊̂ 𝒆 𝒋̂.
2
6 - Encontre o vetor força através dos
ângulos diretores e seu módulo, conforme
a figura ao lado.
R  F = 300 N




F = 212,13 N i + 150 N j - 582,8 N k
7 - (Cap 1 Ex 57 Tipler 6a ed) Determine o módulo, a direção e o sentido




do vetor resultante: D = -2 A + 3 C - 4 B




A = 3,4 i + 4,7 j ,
para:


B = -7,7 i +3,2 j e



C = 5,4 i - 9,1 j
8 - Encontre o valor do vetor força resultante do sistema, sua intensidade
(módulo) e sua direção.



R  F = 113,34 N Fr = -50,64 N i + 101,40 N j  = -63,46o
FC = 60 N
FA = 80 N
25o
36o
36o
FB = 90 N
FA = 80 N
9 – (R. C Hibbeler – Mecânica - Estática – Ex 2.38 p.27) Determine os
vetores força que atuam sobre a caixa e calcule o vetor força resultante, seu
módulo e sua orientação. Considere
que F1 = 500 N e o  = 20º.


R  F = 1030,53 N Fr = 37,42 N i

+ 1.029,85 N j  = 87,92o
3
10 –Denomina-se treliça plana, o conjunto de elementos de construção (barras
redondas, chatas, cantoneiras), interligados entre si, sob forma geométrica
triangular, através de pinos, soldas, rebites, parafusos, que visam formar uma
estrutura rígida, com a finalidade de resistir a esforços normais apenas. A
denominação treliça plana deve-se ao fato de todos os elementos do conjunto
pertencer a um único plano. A sua utilização na prática pode ser observada em
pontes, viadutos, coberturas, guindastes, torres, etc.
Todas as cargas são aplicadas aos nós, normalmente o peso próprio é
desprezado pois a carga suportada é bem maior que o peso do elemento. Para que
o sistema esteja em equilíbrio a resultante das forças em cada nó deve ser nula.
Entretanto um engenheiro ao projetar uma estrutura errou no cálculo do valor do
ângulo , gerando uma força resultante no nó, comprometendo o equilíbrio da
estrutura.
Encontre o valor do vetor força resultante do sistema, sua intensidade e
sua direção.



R  Fr = 362,09 N i + 755,99 N j Fr = 838,23 N  = 64,41o
FA = 8.000 N
35º
50º
FD = 5.000 N
FB = 14.000 N
FC = 12.000 N
11 - (Cap 3 Ex 39 Tipler pág 87) Um urso caminha 60º para nordeste por
12 m e, em seguida, para leste por 12 m. Mostre cada deslocamento
graficamente e obtenha o vetor deslocamento resultante e seu módulo.



R  r = 20,78 m r = 18 m i + 10,39 m j  = 29,97o
12 – (Resnick 5ª ed cap 2 ex 12 ) Um carro é dirigido para o leste por uma
distância de 54 km e, então, para norte por mais 32 km e, finalmente, para uma
direção 28º a noroeste por 27 km. Desenhe o diagrama de vetores e determine o
deslocamento total do carro a partir de seu ponto de partida.



R  r = 53,91 km r = 30,16 km i + 44,68 km j  = 55,98o
4
13 - (Sears & Zemansky – ex. 5.8 p.167) Uma bola grande de um guindaste
de demolição é mantida em equilíbrio por
dois cabos de aço leves. Se a massa m da
bola for igual a 4.090 kg, qual é :
a) a tração TB no cabo que faz um
ângulo de 40º com a vertical?
b) a tração TA no cabo horizontal?
R – T1= 5.000 N
T2=4330,13 N
14 (R. C Hibbeler ) O material granuloso
provoca o carregamento, distribuído sobre a viga
500 N/m
como mostrado na figura ao lado. Determine a
intensidade e a localização da força do material
granuloso.
200 N/m
R  FR = 1.400N
4m
15 - R. C. Hibbeler 2.106 A torre é mantida reta pelos três cabos. Se a força
em cada cabo que atua sobre a torre for aquela mostrada na figura, determine o
vetor força em cada cabo. Considere que x = 20 m, y = 15m.

FDC
=

FDA
=

FDB
=
5