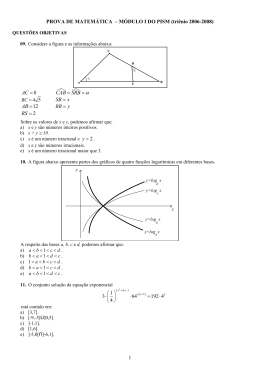
151. (EEAer-2007) Se uma reta passa pelo ponto P(3, 4) e tem coeficiente angular 2, então o
coeficiente linear dessa reta é:
a) - 4
b) - 2
c) 1
d) 3
152. (EEAer-2007) Considere o gráfico da função f : ℝ → ℝ e as afirmativas a seguir:
I) D(f) = ℝ
II) Im(f) = ℝ
III) f(−1) = f(1)
IV) f é crescente no intervalo [1, 3].
y
5
3
-1
1
3
5
x
f
Das 4 afirmativas:
a) todas são verdadeiras.
b) apenas uma é falsa.
c) duas são falsas.
d) apenas uma é verdadeira.
153. (EEAer-2007) Feito um levantamento sobre a altura dos 50 alunos da 5.ª série A de um
colégio, chegou-se aos seguintes resultados:
Altura (cm)
150 |–– 154
154 |–– 158
158 |–– 162
n.º de alunos
6
12
14
Altura (cm) n.º de alunos
162 |–– 166
8
166 |–– 170
6
170 |–– 174
4
Nessas condições, o número de alunos da 5.ª A que não atingem 1,58 m de altura, e a
porcentagem de alunos cuja altura é maior ou igual a 1,62 m são, respectivamente:
a) 12 e 12%.
b) 12 e 20%.
c) 18 e 36%.
154. (EEAer-2007) Se 3 e –3 são duas das raízes da equação x
raízes são:
a) 3i e 2i
b) 2i e –2i
d) 18 e 20%.
4
– 5x
2
– 36 = 0, as outras
c) –i e –3i
1 −1
 −1
1
t
155. (EEAer-2007) Sejam as matrizes A = 
 e B =  0 −3 . Se A e B
2
2




transpostas de A e de B, respectivamente, então At + B t é igual a:
0 2 

0 −1
a) 
2 1

 −2 −3
156. (EEAer-2007) Dois ângulos medem
a) 30
0 2

 −2 −2 
b) 
b) 40
c) 
2π
rad
9
e
5π
18
d) 3i e –3i
t
são as matrizes
0 −1

0 5 
d) 
rad. O menor deles, em graus, mede:
c) 50
d) 60
157. (EEAer-2007) Dois polígonos convexos têm o número de lados expressos por n e por
n + 3. Sabendo que um polígono tem 18 diagonais a mais que o outro, o valor de n é:
a) 10
b) 8
c) 6
d) 4
1
158. (EEAer-2007) O conjunto imagem da função f(x) = 3 + 5sen x é:
a) [-2, 8]
b) [ 3 ,7]
c) [-1, 5]
d) [ 0, 4]
159. (EEAer-2007) Se log 8 = a, então log 3 2 vale:
a)
a
2
b)
a
4
c)
a
9
d)
a
6
160. (EEAer-2007) A medida da altura de um prisma triangular regular é igual à medida da
aresta de sua base. Se a área lateral desse prisma é 10 m 2, então sua altura mede, em m:
a)
15
b)
c)
30
15
d)
2
30
3
161. (EEAer-2008) A soma dos elementos da diagonal principal da matriz A = (aij) 3x3, tal que
 2
a i j=  i se i ≠ j
i + j se i = j
é um número:
a) múltiplo de 3
b) múltiplo de 5
c) divisor de 16
d) divisor de 121
162. (EEAer-2008) O baricentro de um triângulo, cujos vértices são os pontos M (1, 1),
N (3, − 4) e P (− 5, 2), tem coordenadas cuja soma é:
a) 2
b) 1
c) −
2
3
d) −
1
3
163. (EEAer-2008) Em um polígono regular, a medida de um ângulo interno é o triplo da
medida de um ângulo externo. Esse polígono é o:
a) hexágono
b) octógono
c) eneágono
d) decágono
164. (EEAer-2008) Se S = 6ℓ cm 2 é a área de um quadrado de lado ℓ cm, o valor de ℓ é:
a) 3
b) 6
c) 9
d) 12
165. (EEAer-2008) O valor da expressão
a)
1
3
b)
1
2
tg x
,
cos sec x − 1
para 0 < x <
c)
2
3
π
1
e sen x = , é:
2
3
d)
2
8
166. (EEAer-2008) Os pontos A(3, 5), B(4, 3), C(1, 0) e D(0, 4) são vértices de um quadrilátero
ABCD. A área desse quadrilátero é:
a)
15
2
b)
7
2
c) 11
d) 15
167. (EEAer-2008) Seja a circunferência e duas de suas cordas, AB e CD. A medida de CD, em
cm, é:
a) 10
b) 12
c) 14
d) 16
2
168. (EEAer-2008) O número de poliedros regulares que têm faces triangulares é:
a) 1
b) 2
c) 3
d) 4
169. (EEAer-2008) Na figura, AB = AC e BC = CM. O valor de x é:
a) 50°
b) 45°
c) 42°
d) 38°
170. (EEAer-2008) Retirando aleatoriamente um elemento do conjunto A={1, 2, 3, 4,..., 100}, a
probabilidade de ele ser múltiplo de 5 é:
a)
2
5
b)
1
5
c)
1
10
d)
3
10
171. (EEAer-2008) Seja a distribuição de freqüência, onde f i é a freqüência simples absoluta:
A média dessa distribuição é:
a) 10,28
b) 11,17
172. (EEAer-2008) Uma esfera tem 9π cm
raio deve ter sua medida aumentada em:
a)
70
9
%
b)
70
3
c) 13,36
2
d) 14,15
de área. Para que a área passe a 100π cm
%
c)
700
9
%
d)
2
,o
700
%
3
173. (EEAer-2008) A diagonal da secção meridiana de um cilindro equilátero mede10 2 cm.
A área lateral desse cilindro, em cm 2, é:
a) 250π
b) 200π
c) 100π
d) 50π
174. (EEAer-2008) Em um triângulo ABC, retângulo em A, a hipotenusa mede 5 dm e
sen B̂ =
a) 3
1
2
sen Ĉ . Nessas condições, o maior cateto mede, em dm:
b) 4
c) 5
d) 2 5
c) – i
d) – 1
175. (EEAer-2008) Calculando i 2053 , obtém-se:
a) 1
b) i
176. (EEAer-2008) Em um trapézio, a base média mede 6,5 cm e a base maior, 8 cm. A base
menor desse trapézio mede, em cm:
a) 4
b) 5
c) 6
d) 7
177. (EEAer-2008) A raiz real da equação 25
a) 7
b) 5
x
-24 . 5
= 25 é um número múltiplo de:
c) 3
d) 2
x
3
178. (EEAer-2008) Segundo a distribuição de freqüências, o número de funcionários que
ganham a partir de 4 salários mínimos e menos de 10 é:
a) 110
b) 130
c) 185
d) 205
179. (EEAer-2008) No triângulo, cujos lados medem 5cm, 10 cm e 6 cm, o maior ângulo tem
cosseno igual a
a)
7
10
180. (EEAer-2008) Se (x + b)
então o valor de a + b é:
a) 2
9
20
b)
2
c) −
13
20
d) −
8
10
– (x – a)(x + a) ≡ 2x + 17, sendo a e b números reais positivos,
b) 3
c) 5
d) 6
181. (EEAer-2008) Quatro cubos idênticos são dispostos como na figura a seguir, formando um
único sólido. Considerando que a diagonal de cada cubo mede 10 3 cm, a diagonal desse
sólido é, em cm, igual a:
a) 30 3
b) 40 3
c) 20
d) 30
182. (EEAer-2008) Estudando um grupo de crianças de uma determinada cidade, um pediatra
concluiu que suas estaturas variavam segundo a fórmula h = log ( 100,7. i ), onde h é a
estatura (em metros), e i é a idade (em anos). Assim, segundo a fórmula, a estatura de uma
criança de 10 anos dessa cidade é, em m:
a) 1,20
b) 1,18
c) 1,17
d) 1,15
183. (EEAer-2008) A soma dos n primeiros termos da PG (1, – 2, 4, – 8, ... ) é – 85. Logo, n é:
a) 8
b) 10
184. (EEAer-2008) Se 0 < α <
a)
3
3
b)
c) 12
d) 14
π
2
e sen α = , então sen 2α é igual a:
2
3
5
3
c)
4 5
9
d)
4 3
9
185. (EEAer-2008) Para que f(x) = (2m – 6) x + 4 seja crescente em ℝ , o valor real de m deve
ser tal que:
a) m > 3
b) m < 2
c) m < 1
d) m = 0
4
186. (EEAer-2009-BCT) Sejam x, y e b números reais maiores que 1. Se log b x = 2 e log b y = 3,
então o valor de log b ( x². y³ ) é:
a) 13
b) 11
c) 10
d) 8
187. (EEAer-2009-BCT) A aresta da base de um prisma quadrangular regular mede 2 cm. Se a
diagonal desse prisma mede 2 11 cm, sua altura, em cm, mede:
a) 8
b) 6
c) 4
d) 2
188. (EEAer-2009-BCT) São negativas, no 4º quadrante, as funções:
a) seno, cosseno e tangente
b) seno, cosseno e cotangente
c) cosseno, tangente e secante
d) seno, tangente e cossecante
189. (EEAer-2009-BCT) Ao dividir x5 – 3x4 + 2x2 + x + 5 por x – 3, obtém-se um quociente cuja
soma dos coeficientes é
a) 4
b) 6
c) 8
d) 10
190. (EEAer-2009-BCT) Uma lanchonete tem em sua dispensa 5 espécies de frutas.
Misturando 3 espécies diferentes, pode-se preparar ___ tipos de suco.
a) 24
b) 15
c) 10
d) 8
191. (EEAer-2009-BCT) Se x e y são números reais positivos, colog
então x + y é igual a:
a) 2
b) 4
c) 7
2
1
32
=
x e log
y
256 = 4,
d) 9
192. (EEAer-2009-BCT) Sejam uma circunferência de centro O e um ponto A exterior a ela.
Considere AT um segmento tangente à circunferência, em T. Se o raio da circunferência mede
4 cm e AT = 8 2 cm, então a medida de AO , em cm, é:
a) 10
b) 12
c) 13
d) 15
193. (EEAer-2009-BCT) Na figura, OABC é um quadrado de lado 3. Sabendo que o ponto D
tem coordenadas (0, 6), o coeficiente angular da reta r é:
y
D
C
O
a) – 6
B
x
A
b) – 4
c) – 2
d) – 1
194. (EEAer-2009-BCT) Na figura, o ponto P representa um número complexo, cujo conjugado
é:
y
-4
P
a) – 3 + 4i
b) – 4 + 3i
x
-3
c) 4 – 3i
d) 3 – 4i
5
195. (EEAer-2009-BCT) Em um cone, a medida da altura é o triplo da medida do raio da base.
Se o volume do cone é 8π dm3, a medida do raio da base, em dm, é:
a) 0,5
b) 1,5
c) 2
d) 3
196. (EEAer-2009-BCT) Se 3, 5 e – 2, são as raízes da equação 4(x – a)(x – b)(x – 5) = 0, o
valor de a + b é:
a) 0
b) 1
c) 2
d) 3
197. (EEAer-2009-BCT) A área de um setor circular de 30° e raio 6 cm, em cm2, é,
aproximadamente:
a) 7,48
b) 7,65
c) 8,34
d) 9,42
198. (EEAer-2009-BCT) Num triângulo ABC, o ponto médio do lado AB é M(4,3). Se as
coordenadas de B são ambas iguais a 2, então as coordenadas de A são:
a) (7,5)
b) (6,4)
c) (5,3)
d) (3,4)
199. (EEAer-2009-BCT) Quatro números naturais formam uma PG crescente. Se a soma dos
dois primeiros números é 12, e a dos dois últimos é 300, a razão da PG é:
a) 7
b) 5
c) 4
d) 2
200. (EEAer-2009-BCT) Na figura, MN // BC . Se AB = 30 cm, então MB mede, em cm:
8cm C
18cm
N
12cm
A
a) 5
b) 10
M
c) 15
B
d) 20
6