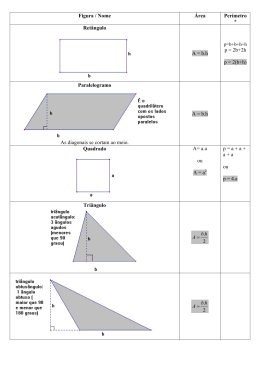
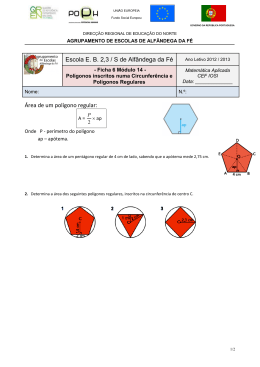
Atividade: REVISÃO TSE
OBS: (ECA 04 – A atividade será verificada em 29/09/2014).
Série: 1ª Série do Ensino Médio
Etapa: 3ª Etapa 2014
Professor: Cadu Pimentel
GEOMETRIA: REVISÃO TSE
ATENÇÃO: Estimados alunos, venho lembrar que somente será aceito o ECA daqueles alunos que
apresentarem todas as soluções completas dos exercícios no caderno. Os exercícios de casa serão anotados
como COMPLETOS (ECA realizado
90%), INCOMPLETOS (50%
ECA realizado
90%) ou NÃO
REALIZADOS (ECA realizado 50%).
01. Na figura, temos uma circunferência inscrita em um hexágono regular. Sem substituir o valor aproximado
de nenhuma raiz, determine o apótema do hexágono regular ABCDEF, sendo o raio da circunferência 4 cm.
02. Determine a medida do apótema de um quadrado inscrito numa circunferência de
de raio.
03. Considere um hexágono regular (H1) ABCDEF e um outro hexágono regular (H2) PQRSTU, onde P é
ponto médio de AB, Q é ponto médio de BC, R é ponto médio de CD e assim sucessivamente até U que é
ponto médio de FA. Neste caso, determine a medida do perímetro de H2, sendo de 48 cm o comprimento da
circunferência circunscrita ao hexágono (H1). Utilize
.
04. (UFPEl–RS - Adaptada) O Brasil é considerado mundialmente o país do futebol.
Em Copas ou em Jogos Olímpicos, esse esporte está sempre presente e muito
orgulho tem trazido para nosso povo, ao receber títulos significativos como o
Pentacampeonato Mundial.
O brasileiro, independentemente de classe econômica, desde cedo tem familiaridade
com a bola de futebol.
Nos cálculos propostos a seguir, suporemos uma bola de couro que possui sua superfície coberta com
pentágonos e hexágonos regulares. Baseando-se em seus conhecimentos e considerando que os hexágonos
que cobrem a bola têm a distância do centro ao ponto médio dos seus lados igual a √
, determine o
perímetro de cada pentágono.
05. A figura abaixo foi cortada de uma cartolina e é formada por um hexágono regular e seis quadrados. Sobre
esta figura sabe-se que a menor diagonal deste hexágono mede √
.
Calcule o raio da circunferência que poderia circunscrever cada um dos quadrados da figura.
06. Um triângulo equilátero está inscrito em uma circunferência inscrita em um quadrado inscrito em uma outra
circunferência inscrita a um hexágono regular. Se o perímetro do hexágono vale 12 cm, determine o perímetro
do triângulo equilátero.
07. Calcule a razão entre o perímetro de uma circunferência inscrita e uma circunferência circunscrita a um
hexágono regular de lado 4 cm.
08. Determine as medidas do lado e do apótema de cada um dos polígonos regulares abaixo:
09. Numa circunferência está inscrito um triângulo equilátero cujo apótema mede 3 cm. A medida do diâmetro
dessa circunferência é:
(A) 6 cm.
(B) 10 cm.
(C) 12 cm.
(D) 42 cm.
(E) 36 cm.
10. O apótema de um triângulo equilátero inscrito numa circunferência mede 8 cm. O lado do hexágono regular
inscrito nessa circunferência mede:
(A)
.
(B) √
.
(C)
.
(D)
√
.
11. Observe a figura abaixo: o perímetro do hexágono regular inscrito na circunferência é
do triângulo equilátero circunscrito a essa mesma circunferência é:
(E)
√
.
. O perímetro
(A) 36 cm.
(B) 90 cm.
(C) 54 cm.
(D) 72 cm.
(E) 48 cm.
12. O lado de um quadrado inscrito em uma circunferência mede
equilátero inscrito nesta mesma circunferência é:
(A)
(B)
(C)
(D)
(E)
√
. A medida do lado do triângulo
√
√
√
√
√
13. Determine, através do Teorema de Tales, a medida de cada incógnita desconhecida:
a)
b)
c)
d)
e)
f)
g)
h)
i)
14. A figura ao lado indica três lotes de terreno com frente para a rua A e para rua B. as divisas dos lotes são
perpendiculares à rua A. As frentes dos lotes 1, 2 e 3 para a rua A, medem, respectivamente, 15 m, 20 m e 25
m. A frente do lote 2 para a rua B mede 28 m. Qual é a medida da frente para a rua B dos lotes 1 e 3?
15. Um feixe de quatro retas paralelas determina sobre uma transversal três segmentos consecutivos, que
medem 5 cm, 6 cm e 9 cm. Calcule os comprimentos dos segmentos determinados pelo feixe em outra
transversal, sabendo que o segmento desta, compreendido entre a primeira e a quarta paralela, mede 60 cm.