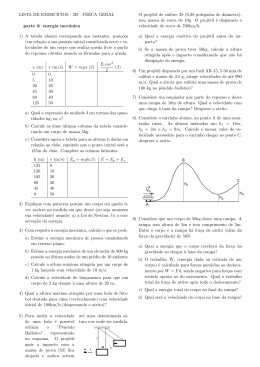
Problemas de Mecânica Clássica
Lic. Fı́sica e Quı́mica–Ramo Educacional
Folha 3 (2003/2004)
1. A figura mostra uma roda de raio r e massa M que sobe um degrau de altura h ao ser puxada
por uma força horizontal aplicada no seu eixo. (The Phys. Teacher 38 (2000) 183-184)
r
F
h
(a) Calcular o valor da força horizontal necessária para inciar essa tarefa.
(b) Discutir os seguintes casos especiais: (i) h = 0; e (ii) h > r.
(c) Dizer, justificando, porque motivo carruagens e veı́culos todo o terreno têm, em geral, rodas
com grandes diâmetros.
2. Considere uma caixa de massa M que se pretende arrastar sobre uma superfı́cie horizontal. Se a
força aplicada actua segundo uma direcção que faz um ângulo θ com a horizontal, como mostra
a figura, qual deve ser a intensidade necessária para iniciar o movimento da caixa sendo µ o
coeficiente de atrito estático. Referir as vantagens de aplicar a força mais horizontalmente ou
mais verticalmente. (The Phys. Teacher 38 (2000) 506-508)
F
θ
3. Um bloco de massa M permanece em repouso sobre um plano que faz um ângulo α com a
horizontal, sob a acção de uma força F~ aplicada horizontalmente como se mostra na figura.
A linha de acção desta força passa pelo centro geométrico do objecto e o coeficiente de atrito
estático é µ. Calcule os valores mı́nimo e máximo de F consistentes com o equilı́brio estático.
F
y
α
α
x
4. Um automóvel descreve uma curva sem inclinação com raio r à velocidade ~v . Admite-se que o
centro de massa, situado à altura H, está simetricamente colocado em relação às rodas. Determinar a velocidade crı́tica para a qual o automóvel tende a capotar, sabendo que a distância
entre as rodas é D. R: vmax = (g r D/(2 H))1/2
5. A figura representa a posição relativa das rodas (massa desprezável) de um automóvel e do
centro de massa do sistema. O automóvel tem tracção às rodas traseiras e arranca sem derrapar
movendo-se da direita para a esquerda. Note que o momento angular das rodas em relação
ao centro de massa é nulo quando se considera que a massa destas é desprezável. Calcular a
aceleração máxima possı́vel do automóvel, sendo µ o coeficiente de atrito estático.
CM
h
b1
b2
6. Um corpo de massa 50 g, partindo do repouso a 1 m de altura, cai no chão e percorre 2 cm,
desde que entra em contacto com o chão até parar. O objectivo do problema consiste em estimar
o tempo de colisão e a força média exercida pelo solo sobre o corpo. Clarificar as leis fı́sicas
relevantes na resolução do problema. Referir as vantagens do uso do princı́pio do impulsoquantidade de movimento. A resolução do problema poderá também ser baseada no teorema da
trabalho-energia cinética? Justificar.
7. Um projéctil de chumbo de 19 g movia-se com velocidade 100 m/s no instante em que penetrou
num bloco de madeira de espessura 10 cm, saindo com a velocidade de 20 m/s. A variação de
energia interna do projéctil é de 8 J.
Responder às questões abaixo indicadas referindo os processos de transformação de energia que
ocorrem no sistema, bem como a utilidade do modelo de centro de massa.
(a) Verificar que não há conservação da energia mecânica.
(b) Calcular o trabalho da força que o bloco exerce sobre o projéctil. Justificar detalhadamente
todos os cálculos.
(c) Determinar o valor médio da força exercida pelo bloco sobre o projéctil.
8. Uma bola metálica de massa 5, 2 g é lançada verticalmente, de cima para baixo, de uma altura
h1 = 18 m com velocidade inicial v0 = 14 m/ s. Depois de percorrida a distância h1 o objecto
enterra-se na areia, imobilizando-se à profundidade h2 = 21 cm como mostra a figura. Desprezar
a força de resistência do ar.
Responda às questões abaixo indicadas explicitando claramente as leis fı́sicas em que fundamenta
a sua resposta.
m
v0
h1
h2
(a) Qual a variação da energia mecânica da bola?
(b) Qual a variação da energia interna do sistema bola-Terra-areia?
(c) Qual a intensidade da força média exercida pela areia sobre a bola?