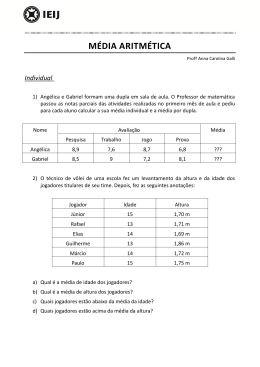
Onde:
πi (s*i , s*-i) > π (si , s*-i), para todo si e todo s-i => Equilíbrio de Nash28
Ou seja, é interessante para M adotar 1/1, ou seja cooperarem para o caso de os seus respectivos subgrupos {a,...d} alterem suas posições.
Perceba que nossos exemplos acima foram representados somente pela categoria de jogos
simultâneos. Isso se deve a necessidade imperativa de analisar situações onde a maioria e a minoria devem tomar suas decisões ao mesmo tempo. Entretanto, a realidade numa situação política
é de uma interação repetida desses jogos, e não apenas a existência de um único jogo de estratégias: ao contrário, na vida política tais jogos resultam, em etapas que se repetem. Levando, os jogadores (M, m) a apreciarem o resultado da etapa antecedente, mas ignorarem as etapas seguintes,
onde serão chamados a decidir novamente29.
Conforme já compreendido, certos jogos infinitamente repetidos, ao se levar em conta a
recompensa dos jogadores, e tomando por certo o fator de desconto30 como elevado, a cooperação
pode ser sustentada em longo prazo. Caso M e m adotem uma estratégia gatilho31, isto pode ser
perfeitamente viável.
Conclusão
Hans Kelsen procurou em sua obra a democracia, aplicar o desenvolvimento de sua teoria
que explique o fenômeno democrático em consonância com sua teoria pura, adotando um relativismo político como fundamento.
Ao longo de sua obra pressupõe solucionar a falsa dicotomia entre liberdade e igualdade,
para ele pressupostos fundamentais do homem político. Para solucionar tal dicotomia, ele vai construindo através de um diálogo ainda que velado com os grandes contratualistas do passado: Hobbes, Locke e Rosseau. E quanto ao último faz ceder não só a crítica que este fez a dominação, mas
também à ausência de representação da vontade do particular pela vontade geral.
Quanto à dominação, Kelsen sustenta que a dominação democrática é válida. Se formos
dominados – ele sustenta – deveremos ser por nós mesmos, através da regra da maioria para que
haja um contrato social estável e duradouro.
Quanto à idéia de liberdade, este não concorda com a afirmação que a liberdade seja causal
e natural. Para a obtenção da paz social almejada, temos que traduzir a liberdade como um conceito relativo e político.
Conforme já observado, o princípio do voto majoritário é a chave não só da vontade geral (e
liberdade política) como também o fundamento da democracia. Entretanto, a limitação da atuação
do princípio democrático da maioria deve se assentar no respeito aos direitos fundamentais das
minorias resultantes do processo democrático, instituídos em uma carta constitucional.
O equilíbrio de Nash, conforme apresentado, vêm confirmar não só em jogos de estratégias
simultâneos, mas também em sua modalidade de repetição a sustentabilidade do respeito aos direitos humanos no projeto democrático da teoria pura.
28
Nota do autor: Onde a função de recompensa do jogador πi, as suas jogadas são apresentadas como si, e as estratégias de
outros jogadores que não i são –i. O asterisco (*) é sinal de equilíbrio nashiano.
29
Nota do autor: Sugerimos a leitura do capítulo “a regra do jogo” sobre a adoção da estratégia tit-for- tat. SAGAN, Carl.
Bilhões e Bilhões: reflexões sobre vida e morte na virada do milênio. São Paulo: Companhia das letras, 1998. p.197-209.
30
“Contudo, conforme tivemos oportunidade de ver ao analisar negociações de barganha, no capítulo anterior, receber um
real hoje é algo diferente de receber um real amanhã. Na verdade, receber $1 hoje é melhor que receber $1 amanhã, no sentido preciso de que $1 amanhã vale um pouco menos do que hoje. Em outras palavras, precisamos descontar um valor futuro (o recebimento
de um real amanhã), para atualizarmos esse valor futuro, isto é, para trazê-lo ao valor presente. Para isso, precisamos aplicar ao
recebimento futuro, ou futura recompensa, um fator de desconto.” FIANI, Ronaldo. Teoria dos Jogos. idem. p.160.
31
“Uma estratégia gatilho é uma estratégia que determina, para o jogador que a adota, seguir um curso de ação enquanto
uma determinada condição é satisfeita e, caso essa condição em qualquer momento deixe de ser satisfeita, seguir um outro curso
de ação pelo resto do jogo.” FIANI, Ronaldo. Teoria dos Jogos. idem. p.163.