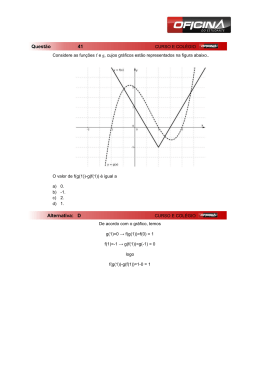
▼
Questão 61
Considere a função
f(x) = 1 –
4x
,
(x + 1) 2
a qual está definida para x ≠ –1. Então, para todo x ≠ 1 e x ≠ 1, o produto f(x) f(–x) é igual a
a) –1
b) 1
c) x + 1
d) x2 + 1
e) (x – 1) 2
Resolução
Para todo x ≠ 1 e x ≠ –1, tem-se:
f(x) = 1 –
4x
(x + 1)2 – 4x (x – 1)2
=
=
(x + 1)2
(x + 1)2
(x + 1)2
e
f(–x) = 1 +
4x
4x
(x – 1)2 + 4x (x + 1)2
=1+
=
=
2
2
(x – 1)2
(1 – x)
(x – 1)
(x – 1)2
Portanto,
f(x) ⋅ f(–x) =
Resposta: b
(x – 1)2 (x + 1)2
⋅
=1
(x + 1)2 (x – 1)2