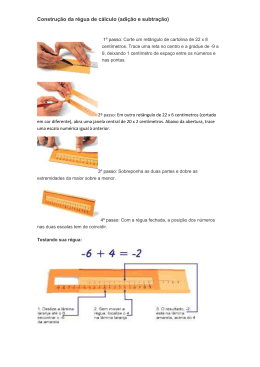
Aproximando a medida do pi
Objetivos: Obter uma aproximação decimal para a constante pi.
Descrição: O objeto propõe uma atividade prática que permitirá aos alunos a obtenção de um
valor aproximado a pi.
Material Necessário: Lápis, borracha, calculadora, régua, barbante (novelo), tesoura, folhas
de ofício (ou cartolina) e compasso.
1º momento - desenhando circunferências:
 Cada aluno deverá desenhar com o compasso, em suas folhas de ofício, três
circunferências de raios distintos (Uma sugestão de medidas de raio: 5, 10 e 15
centímetros, sendo a de 15 centímetros em uma folha maior, talvez uma cartolina, já
que o diâmetro será de 30 centímetros).
 Uma forma de conseguirmos raios diferentes é traçando segmentos de reta com o
auxílio da régua, identificando algumas medidas, por exemplo, 5, 10 e 15 centímetros
cada. Com essas medidas, o aluno pode traçar as circunferências com o compasso. É
importante que o centro delas seja marcado, para que o raio de cada circunferência
fique evidente.
2º momento – registrando medidas:
 Em cada caso desenhado, com o auxílio do barbante e da régua, os alunos irão medir o
comprimento e o diâmetro de cada circunferência, registrando na tabela abaixo, que
deve ser distribuída a cada aluno:
Comprimento da
Circunferência
Diâmetro D (2 raios)
Valor Obtido pela divisão:
Comprimento
Diâmetro(2r )
3° momento – Obtenção do valor aproximado para pi:
 Feito o registro dos valores obtidos para medidas aproximadas do comprimento e do
diâmetro, agora a tarefa será a obtenção de um valor aproximado para pi. O método
consiste em tomar o valor da medida do comprimento de uma circunferência e dividilo pelo valor da medida do seu diâmetro, obtendo assim um valor próximo de 3. Neste
momento, a turma poderá utilizar calculadora como ferramenta auxiliar para a divisão.
 O número obtido deverá ser registrado na terceira coluna da tabela anterior. O valor
encontrado após a realização das divisões é uma aproximação à constante pi.
 Note que esta atividade poderá gerar um alto grau de imprecisão, o que não caracteriza
um problema, pois poderá ser um assunto discutido com os próprios alunos.
 Sugerimos que o professor não revele este fato aos alunos, de que o número resultante
desta divisão é muito próximo de uma constante.
 Podem ser lançadas perguntas aos alunos, como por exemplo "O que há de semelhante
ou de diferente entre os resultados?", auxiliando os alunos a perceberem que
encontraram uma aproximação para a constante pi.
 Uma vez que os alunos compreendam o significado da divisão, o professor pode
continuar o diálogo perguntando: "Isso acontece para qualquer circunferência que
traçamos? Por que isso acontece?".