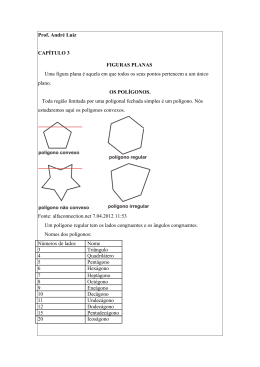
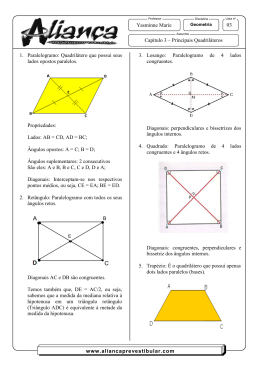
2ª série - REVISÃO Prova - 26 de abril 2ª chamada – 29 de abril Professor Cezar [email protected] Nome dos polígonos De acordo com o número de n lados, os polígonos recebem nomes especiais. Veja a seguir as correspondências: n= n= n= n= n= n= n= n= n= n= n= n= n= n= n= n= n= n= 3 triângulo ou trilátero 4 quadrângulo ou quadrilátero 5 pentágono 6 hexágono 7 heptágono 8 octógono 9 eneágono 10 decágono 11 undecágono 12 dodecágono 13 tridecágono 14 tetradecágono 15 pentadecágono 16 hexadecágono 17 heptadecágono 18 octodecágono 19 enedecágono 20 icoságono O número de diagonais d de um polígono de n lados (n 3) é dado por: d n(n 3) 2 A soma dos ângulos internos de um polígono convexo é: Si (n 2) 180 º Expressão do ângulo interno de um polígono regular ai Si n ai 180 º (n 2) n Colégio Maxi www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar Rua Estevão de Mendonça, 1000 Bairro Quilombo Cuiabá – MT CEP 78043-405 Fone (65) 3614-5454 2ª série - REVISÃO Prova - 26 de abril 2ª chamada – 29 de abril Professor Cezar [email protected] O número de diagonais que passam pelo centro dPC de um polígono de n lados (n par) é dado por: n 2 dPC d total de diagonais de um polígono Consideran do dPC diagonais que passam pelo centro temos d NPC diagonais que não passam pelo centro d dPC dNPC Cálculo de lado e apótema dos polígonos regulares em função do raio r da circunferência circunscrita l4 r 2 a4 r 2 2 l6 r a6 r 3 2 l3 r 3 a3 r 2 Colégio Maxi www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar Rua Estevão de Mendonça, 1000 Bairro Quilombo Cuiabá – MT CEP 78043-405 Fone (65) 3614-5454 2ª série - REVISÃO Prova - 26 de abril 2ª chamada – 29 de abril Professor Cezar [email protected] Quadriláteros Notáveis Trapézio Um quadrilátero plano convexo é um trapézio se, e somente se, possui dois lados paralelos Os lados paralelos são as bases do trapézio De acordo com os outros dois lados não bases temos: trapézio isósceles, se estes lados são congruentes trapézio escaleno, se estes lados não são congruentes trapézio retângulo é um retângulo que tem dois ângulos retos. Paralelogramo Um quadrilátero plano convexo é um paralelogramo se, e somente se, possui os lados opostos paralelos. Retângulo Um quadrilátero plano convexo é um retângulo se, e somente se, possui os quatro ângulos congruentes. Colégio Maxi www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar Rua Estevão de Mendonça, 1000 Bairro Quilombo Cuiabá – MT CEP 78043-405 Fone (65) 3614-5454 2ª série - REVISÃO Prova - 26 de abril 2ª chamada – 29 de abril Professor Cezar [email protected] Losango Um quadrilátero plano convexo é um losango se, e somente se, possui os quatro lados congruentes Quadrado Um quadrilátero plano convexo é um quadrado se, e somente se, possui os quatro ângulos congruentes e os quatro lados congruentes. Propriedades dos paralelogramos 1) Em todo paralelogramo dois ângulos opostos quaisquer são congruentes. 2) Todo quadrilátero convexo que tem ângulos congruentes é paralelogramo. Todo retângulo é paralelogramo 3) Em todo paralelogramo, dois lados opostos quaisquer são congruentes. 4) Todo quadrilátero convexo que tem lados opostos congruentes é paralelogramo. Todo losango é paralelogramo 5) Em todo paralelogramo, as diagonais interceptam-se nos respectivos pontos médios. 6) Todo quadrilátero convexo em que as diagonais interceptam-se nos respectivos pontos médios é paralelogramo. 7) Todo quadrilátero convexo que tem dois lados paralelos e congruentes é um paralelogramo. 8) Em todo retângulo as diagonais são congruentes 9) Todo losango tem diagonais perpendiculares. Todo quadrado é retângulo e também losango Colégio Maxi www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar Rua Estevão de Mendonça, 1000 Bairro Quilombo Cuiabá – MT CEP 78043-405 Fone (65) 3614-5454 2ª série - REVISÃO Prova - 26 de abril 2ª chamada – 29 de abril Professor Cezar [email protected] Bases Médias Base média do triângulo Se um segmento tem extremidade nos pontos médios de dois lados de um triângulo, então: a) ele é paralelo ao terceiro lado; b) ele é metade do terceiro lado. BC MN 2 Base média do trapézio Se um segmento tem extremidade nos pontos médios dos lados não paralelos de um trapézio, então: c) ele é paralelo às bases; d) ele é igual à semi-soma das bases. AB CD MN 2 Áreas de figuras planas Quadriláteros Quadrado Dado um quadrado de lado a temos: AQuadrado a 2 Retângulo Dado um retângulo de lado b (base) e lado h (altura) temos: ARe tângulo b h Paralelogramo Dado o paralelogramo de lado b (base) e altura h, ele é equivalente a um retângulo cuja base mede b e altura mede h. Logo: AParale log ramo b h Colégio Maxi www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar Rua Estevão de Mendonça, 1000 Bairro Quilombo Cuiabá – MT CEP 78043-405 Fone (65) 3614-5454 2ª série - REVISÃO Prova - 26 de abril 2ª chamada – 29 de abril Professor Cezar [email protected] Losango Dado o losango cujas diagonais perpendiculares são representadas por D (diagonal Dd maior) e d (diagonal menor), temos: ALosango 2 Trapézio Dado o trapézio com as bases B (base maior) e b (base menor) e a distância entre (B b) h as bases h (altura), temos: ATrapézio 2 Expressões da área do triângulo Em função dos lados e respectivas alturas: ATriângulo b h 2 Área do triângulo eqüilátero de lado a com altura h l 3 l2 3 : ATriângulo 2 4 Área do triângulo em função dos lados: abc Dados: lados a, b e c e com p , temos: ATriângulo p(p a)(p b)(p c) 2 Área do triângulo em função dos lados e do raio r da circunferência inscrita. abc Dados: lados a, b e c e com p , temos: ATriângulo p r 2 Área do triângulo em função de dois lados a e b e ângulo compreendido: 1 ATriângulo a b sen 2 Hexágono Um hexágono regular de lado a é a reunião de 6 triângulos eqüiláteros de lado a. 3 3 2 AHexágono a 2 Colégio Maxi www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar Rua Estevão de Mendonça, 1000 Bairro Quilombo Cuiabá – MT CEP 78043-405 Fone (65) 3614-5454
Baixar