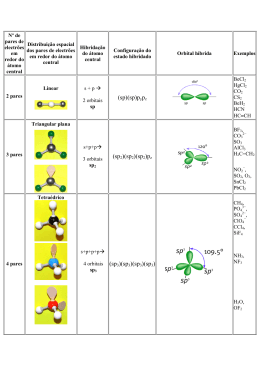
Moléculas poliatómicas: CH4
Molécula tetraédrica
(4 ligações equivalentes!)
OA’s não dão!
(ângulos de 90º)
H H
C
H
H
109.47º
H
H
θ
θ
C
C
θ
H
H
H
=
θ
C
H
θ = 109º 28´
H
H
TEV
Hibridação
TEV
Combinações lineares de OA’s
(mesmo n, R(r) semelhante)
p.e.: uma orbital s e uma orbital p
sp
s
p
s+p
sp
sp
sp
sp
ou, na representação
simplificada
s-p
sp
s±p
redistribuição da
núvem electrónica
2 orbitais sp
parte-se de N OA’s → chegam-se
a N orbitais híbridas
1
(Ψs + Ψ p )
Ψsp′ =
2
Ψsp′ =
1
(Ψs − Ψ p )
2
Hibridação
Se forem duas orbitais p:
TEV
+
−
+
-
+
p±p
direcção espacial da
núvem electrónica
É como somar vectores…
Hibridações
sp
(
1
Ψs ± Ψ p
x
2
)
Geometria linear
2 orbitais!
Hibridações
sp2
y
(
1
Ψs + 2 Ψ p x
3
)
x
⎞
1 ⎛
1
3
⎜ Ψs −
⎟
Ψ
±
Ψ
p
p
x
y
⎟
2
2
3 ⎜⎝
⎠
Geometria triangular plana
…não tem pz…
3 orbitais!
Hibridações
sp3
(
)
(
)
1
Ψs + Ψ p x − Ψ p y − Ψ p z
2
1
Ψs + Ψ p x + Ψ p y + Ψ p z
2
(
)
(
)
1
Ψs − Ψ p x + Ψ p y − Ψ p z
2
1
Ψs − Ψ p x − Ψ p y + Ψ p z
2
z
y
x
Geometria tetraédrica
4 orbitais!
Hibridações
dsp2
1⎛
⎜Ψs + Ψd 2 2 + 2 Ψpx ⎞⎟
x −y
⎠
2⎝
1⎛
⎜Ψs +Ψd 2 2 − 2 Ψpx ⎞⎟
x −y
⎠
2⎝
y
1⎛
⎜Ψs −Ψd 2 2 + 2 Ψpy ⎞⎟
x −y
⎠
2⎝
1⎛
⎜Ψs −Ψd 2 2 − 2 Ψpy ⎞⎟
x −y
⎠
2⎝
…sem pz e com dx2-y2…
x
Geometria quadrangular plana
4 orbitais!
Hibridações
dsp3
(
1
Ψs + 2 Ψ p x
3
)
⎞
1 ⎛
1
3
⎜ Ψs −
Ψpx +
Ψ p y ⎟⎟
⎜
2
2
3⎝
⎠
z
⎞
1 ⎛
1
3
⎜ Ψs −
Ψpx −
Ψ p y ⎟⎟
⎜
2
2
3⎝
⎠
(
1
Ψ p z + Ψd 2
z
2
(
1
Ψ pz − Ψd 2
z
2
x
)
y
)
a s, as três p e mais uma d
Geometria bipirâmide trigonal
5 orbitais!
d2sp3
Hibridações
(
1
Ψs + 2Ψd 2 + 3Ψ p z
z
6
)
⎞
1 ⎛
1
3
⎜ Ψs −
Ψd 2 +
Ψd x 2 − y 2 + 3Ψ p x ⎟⎟
⎜
z
2
2
6⎝
⎠
⎞
1 ⎛
1
3
⎜ Ψs −
⎟
Ψ
−
Ψ
+
Ψ
3
d 2
d x2 − y2
py ⎟
⎜
z
2
2
6⎝
⎠
⎞
1 ⎛
1
3
⎜ Ψs − Ψd + Ψd x2 − y 2 − 3Ψp ⎟
x⎟
2 z2
2
6 ⎜⎝
⎠
z
x
y
⎞
1 ⎛
1
3
⎜ Ψs −
⎟
Ψ
−
Ψ
−
Ψ
3
2
2
d 2
d x −y
py ⎟
⎜
z
2
2
6⎝
⎠
(
1
Ψs + 2Ψd 2 − 3Ψ p z
z
6
)
a s, as três p e mais duas d
6 orbitais!
Geometria octaédrica
Hibridações
O que determina a hibridação de um “átomo central” (A)?
Número de direcções independentes no espaço
(em torno de A) em que existem pares de e-’s.
Partilhados ou não!
Será precisa uma orbital híbrida para cada direcção
(i.e., para cada par de e-’s)
Parte-se de igual número de OA’s
CH4
TEV
H H
C
H
H
Nº de direcções em torno de C =
4
Nº de orbitais híbridas =
4
Nº de orbitais atómicas de partida =
4
Quais ?
Todas as de valência (só tem 4):
a 2s e as três 2p (2px, 2py e 2pz)
Combina-se uma orbital s com três orbitais p:
obtêm-se quatro orbitais sp3.
conf. electrónica do átomo isolado
C 2s2 2px1 2py1 2pz0
conf. electrónica do átomo na molécula (valência)
C (sp3)1(sp3)1(sp3)1(sp3)1
CH4
TEV
C 2s2 2px1 2py1 2pz0
C
(sp3)1(sp3)1(sp3)1(sp3)1
Promoção de um e- compensada
pela formação de uma ligação
H 1s1
Quatro ligações σ:
(sp3)C1 – (1s)H1
1s
H
H
sp3
H
H
C2H4, etileno
H
C
H
3 direcções em torno de cada C
TEV
H
C
H
C 2s2 2px1 2py1 2pz0
3 orbitais híbridas
3 orbitais atómicas de partida
C (sp2)1(sp2)1(sp2)1pz1
a s (dá jeito: é esférica) e duas p
sp2
Não foi usada
(perpendicular ao plano das sp2)
y
x
sp2
pz
C2H4, etileno
H
H
H
C
1s1
H
H
C 2s2 2px1 2py1 2pz0
H
H
TEV
H
H
Ligação C=C
dupla: σ + π
C
Promoção de um e- compensada
pela formação de uma ligação
C (sp2)1(sp2)1(sp2)1pz1
Cada C usa as orbitais sp2 para fazer três ligações σ:
duas ligações (sp2)C1 – (1s)H1
e uma ligação (sp2)C1 – (sp2)C1
As orbitais pz dos dois C orientam-se de forma a
ficarem paralelas e a formarem uma ligação π:
(pz)C1 - (pz)C1
z
H
1s
pz
H
C
C
x
sp2
H
H
Isómeros geométricos
z
z
Rotação impedida:
quebra da ligação π
Cl
H
C
Cl
µ= 0
Cl
C
C
H
trans
Cl
C
H
H
cis µ = 0
C2H2, acetileno
2 direcções em torno de cada C
2 orbitais híbridas
2 orbitais atómicas de partida
uma s e uma p
sp
H
C
C
TEV
H
C 2s2 2px1 2py1 2pz0
C (sp)1(sp)1py1pz1
Não foram usadas
(perpendiculares às sp)
sp
py
pz
C2H2, acetileno
H
C
C
C
H 1s1
C 2s2 2px1 2py1 2pz0
Promoção de um e- compensada
pela formação de uma ligação
C (sp)1(sp)1py1pz1
Cada C faz duas ligações σ:
(sp)C1 – (1s)H1
(sp)C1 – (sp)C1
z
pz
1s
sp
H
C
y
C
x
sp
py
H
TEV
H
H
Ligação C≡C
tripla: σ + 2π
e duas ligações π:
(py)C1 – (py)C1
(pz)C1 – (pz)C1
C
H
C
H
H
C
C
H
H
H
H
C
H
H
C
H
H
-1
H
Energia de Ligação (kcal mol )
Multiplicidade da ligação C–C
200
150
100
50
1.1
1.2
1.3
1.4
1.5
1.6
Comprimento de Ligação (Å)
Molécula Tipo de ligação Energia de ligação Comprimento da
C-C / kcal mol-1
ligação C-C /Å
C2H6
σ
83,1
1,54
C2H4
σ, π
148
1,34
C2H2
σ, 2π
194
1,20
Ligações π mais fracas que ligações σ
Direccionalidade das orbitais híbridas
Aumenta com o carácter s das orbitais híbridas
Orbitais sp: 50% de s
+
> direccionalidade > densidade electrónica >
> coalescência → ligações + fortes!
Molécula
Hibridação Energia da ligação Distância
C-H / kcal mol-1
Internuclear C-H /Å
H-C≡C-H
sp
~121
1,06
H2C=CH2
sp2
~106
1,07
CH4
sp3
98
1,09
Radical CH
~p
~80
1,12
Electronegatividade de orbital
Electronegatividade
O
Aumenta com % carácter s das orbitais híbridas
4,0
N
C
3,0
2,0
0
sp3 sp2
20
40
sp
60
80
% de carácter s
Ex.: “Acidez” de alcinos terminais:
R
C
C
(pKa(C2H2) = 25)
H + NaNH2
R
C
C Na
+ NH3
H2O
H 1s1
O 2s2 2px2 2py1 2pz1
O (sp3)2(sp3)2(sp3)1(sp3)1
Duas ligações σ:
(sp3)O1 – (1s)H1
TRPECV:
4 pares de e-’s em volta do O
(2×1 + 6)/2
Dois pares de e-’s
não partilhados:
(sp3)O2
Geometria
tetraédrica
pares não partilhados
(pares de e-’s)
4 direcções com
pares de e-’s
sp3
H
H
H2O
Molécula polar
pares não partilhados
µ
H
H
NH3
H 1s1
N 2s2 2px1 2py1 2pz1
N (sp3)2(sp3)1(sp3)1(sp3)1
Três ligações σ:
(sp3)N1 – (1s)H1
TRPECV:
4 pares de e-’s em volta do N
(3×1 + 5)/2
Um par de e-’s
não partilhados:
(sp3)N2
Geometria
tetraédrica
(pares de e-’s)
H
4 direcções com
pares de e-’s
sp3
par
não-partilhado
1s
sp3
H
H
NH3
Molécula polar
µ
resultante
H
µ
par não partilhado
N
θ = 107º
sp3
H
H
par
não-partilhado
1s
H
H
S
P −1
=
cos θ =
S −1
P
69% p e 31% s
S % de s
P % de p
70% p e 30% s
H H
N
C
H
H
109.47º
sp3 “pura”:
75% p e 25% s
H
107º
H
H
77% p e 23% s
O
H
H
104.5º
80% p e 20% s