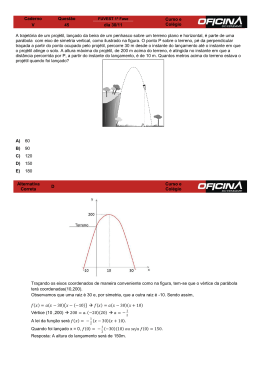
9 - LANÇAMENTO DE PROJÉTIL
1
FEX 1001
Objetivos
Vericar a cinemática do movimento de um projétil. Determinar a velocidade de lançamento de um projétil, tendo medido
o seu alcance para diferentes alturas de lançamento. Vericar que a trajetória do movimento é parabólica.
2
Teoria
Quando lançamos um pequeno objeto, como uma pedra, observamos que seu movimento pode ser descrito como dois
movimentos retilíneos independentes: um na vertical e um na horizontal. Ambos os movimentos estão sujeitos a ação
das forças peso e resistência do ar. Considerando uma situação na qual o ar esteja em repouso em relação ao solo (sem
vento) esta força de resistência atua na direção contrária ao movimento, enquanto a força peso atua na direção vertical
e para baixo. Se a distância de lançamento for relativamente pequena, poderemos desconsiderar o movimento de rotação
da Terra, e se o objeto lançado não for leve o suciente para sentir a força de resistência do ar, poderemos, com boa
aproximação, considerar o movimento horizontal como um movimento retilíneo e uniforme. Então, os dois movimentos
independentes são: um movimento retilíneo uniforme (MRU) na direção ox e um movimento uniformemente acelerado
(MRUV) na direção oy . Pelas equações da cinemática podemos escrever
x
(2.1)
= xo + vox t ,
2
y
= yo + voy t +
at
2
(2.2)
,
conhecidas como equações paramétricas da trajetória do projétil. Nestas equações (x, y ) são as coordenadas1 do projétil
e dão a sua posição num dado instante, medidas em relação a algum sistema de referência. O valor do par (xo , yo )
corresponde a posição inicial de lançamento do projétil, medido no mesmo sistema de referência. Como o projétil
é lançado como velocidade diferente de zero e numa direção qualquer, então (vox , voy ) são os componentes deste vetor
velocidade inicial. Estes componentes são dados em termos do módulo da velocidade inicial, Vo , e do ângulo de lançamento
θo , ambos mostrados na gura 2.1 abaixo.
y
v oy
vo
θο
yo
0
Figura 2.1:
v ox
x
xo
Diagrama ilustrativo do lançamento de um projétil. Os componentes do vetor velocidade inicial são
vox =
Vo cosθo e voy = Vo senθo . A posição inicial é marcada pelo par (xo , yo ) em relação à origem O.
3
Descrição do Experimento
O equipamento utilizado neste experimento é um dispositivo de lançamento, montado sobre uma placa suporte na qual
podem ser escolhidas diferentes alturas e diferentes ângulos para o lançamento da bola. Também podem ser escolhidas
diferentes velocidades de lançamento através da elongação de uma mola, que se encontra no interior do disparador.
Medindo-se o alcance e a altura de voo, pode-se determinar a velocidade de lançamento da bola. A gura 3.1 abaixo
ilustra o aparato experimental. Observe que algumas medidas já estão indicadas na gura para a devida escolha do
sistema de referência. As alturas de lançamento são, medidas de baixo para cima a partir da base de lançamento, 50 mm,
100 mm, 150 mm, 200 mm e 300 mm, e correspondem a altura de lançamento do centro da esfera.
1 O ponto (x, y ) também pode ser representado por (x(t), y(t)) para reforçar a informação que estas coordenadas estão parametrizadas pelo
tempo. O ponto inicial (xo , yo ) ca representado por (x(t = 0), y(t = 0)), ou simplesmente, (x(0), y(0)).
1
1
xm
108 mm
h = 200mm
2
3
Figura 3.1:
Aparato experimental: 1-dispositivo de lançamento (disparador); 2-posição de lançamento da bola; 3-papel
comum e papel carbono. Observe que, ao tocar a mesa, o centro da esfera encontra-se a altura r (raio da esfera) acima
da mesa.
4
Equipamento/Material
1. Papel branco e papel carbono.
2. Trena.
3. Fita adesiva.
4. Esfera, lançador e bastão.
5. Torre de lançamento.
5
Procedimento Experimental
(a)
Coloque o dispositivo de lançamento inicialmente na inclinação de zero grau e escolha um sistema de referência am
de medir, neste sistema, a altura inicial de lançamento, a altura nal e o alcance do centro da esfera.
(b)
Lance a bola para cada uma das cinco alturas de lançamento (50 mm, 100 mm, 150 mm, 200 mm e 300 mm medidas
a partir da base de lançamento) medindo para cada uma delas o alcance da bola e anotando todos os dados na
tabela da folha de questões. Ou seja, para cada lançamento, indique a posição inicial (xo, yo ) do centro da esfera e
sua posição nal (x, y) completando a tabela.
(c)
Responda às questões da folha de relatório.
2
FEX 1001
9 - LANÇAMENTO DE PROJÉTIL
Indicar todas as alturas e todos os alcances em centímetro. Use g = 9, 81 m/s2
x1o =
x1 =
h1 = 50, 0mm
y1o =
y1 =
x2o =
x2 =
h2 = 100, 0mm
y2o =
y2 =
x3o =
x3 =
x4o =
x4 =
h4 = 200, 0mm
y4o =
y4 =
x5o =
x5 =
h5 = 300, 0mm
y5o =
y5 =
h3 = 150, 0mm
y3o =
y3 =
1. Com base no experimento e na escolha das grandezas físicas que foram medidas (altura de lançamento H
e alcance R), responda qual é a variável independente e qual é a variável dependente, justicando sua
resposta.
2. Observando que R = x − xo e H = y − yo , complete a tabela abaixo.
R1 =
h1 = 50, 0mm
H1 =
R4 =
R2 =
h4 = 200, 0mm
H4 =
h2 = 100, 0mm
H2 =
R5 =
R3 =
h5 = 300, 0mm
H5 =
h3 = 150, 0mm
H3 =
3. Sabendo que a relação entre as grandezas envolvidas, R e H , é dada por R2 = −
equação mostrando claramente os coecientes angular e linear da reta.
2vo2
H , linearize esta
g
4. Com base na sua linearização, trace um gráco linear em papel adequado e obtenha, a partir do seu
gráco, a velocidade inicial de lançamento, vo , da esfera. Mostre todos os cálculos com clareza.
5. Calcule o erro percentual no valor obtido para vo com relação ao valor fornecido pelo fabricante
(vo = 3, 53 m/s).
6. Escreva a equação do erro propagado na velocidade lançamento e calcule o correspondente Valor. Para
isto, observe que ∆R = ∆H = 0, 0005m e conside g como constante de precisão innita.
3