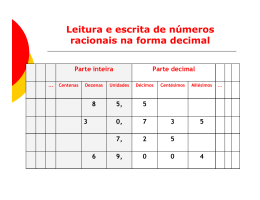
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
Padrões de Desempenho Estudantil
Abaixo do Básico
Básico
Proficiente
Os Padrões de Desempenho são categorias definidas a partir de
cortes numéricos que agrupam os níveis da Escala de Proficiência,
com base nas metas educacionais estabelecidas pelo SAEGO. Esses
cortes dão origem a quatro Padrões de Desempenho, os quais
apresentam o perfil de desempenho dos estudantes
Abaixo do Básico
Avançado
Além disso, as competências e
habilidades agrupadas nos Padrões
não esgotam tudo aquilo que os
estudantes desenvolveram e são
capazes de fazer, uma vez que as
habilidades avaliadas são aquelas
consideradas essenciais em cada
Básico
Proficient
Avançado
etapa de escolarização e possíveis
de serem avaliadas em um teste
de múltipla escolha. Cabe aos
docentes, através de instrumentos
de observação e registros
Desta forma, estudantes que se encontram em um Padrão de
utilizados em sua prática cotidiana,
Desempenho abaixo do esperado para sua etapa de escolaridade
identificarem outras características
precisam ser foco de ações pedagógicas mais especializadas, de
apresentadas por seus estudantes
modo a garantir o desenvolvimento das habilidades necessárias ao
e que não são contempladas nos
sucesso escolar, evitando, assim, a repetência e a evasão.
Padrões. Isso porque, a despeito
Por outro lado, estar no Padrão mais elevado indica o caminho
para o êxito e a qualidade da aprendizagem dos estudantes.
Contudo, é preciso salientar que mesmo os estudantes
posicionados no Padrão mais elevado precisam de atenção, pois é
necessário estimulá-los para que progridam cada vez mais.
dos traços comuns a estudantes
que se encontram em um mesmo
intervalo de proficiência, existem
diferenças individuais que
precisam ser consideradas para a
reorientação da prática pedagógica.
São apresentados, a seguir, exemplos de itens* característicos de cada Padrão.
*O percentual de respostas em branco e nulas
não foi contemplado na análise.
Abaixo do Básico
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
500
até 225 pontos
Nesse Padrão de Desempenho, as habilidades matemáticas que se evidenciam são as relativas aos
significados dos números nos diversos contextos sociais, na compreensão dos algoritmos da adição
de números de até três algarismos com reagrupamento, da subtração de até quatro algarismos com
reserva, da multiplicação de até dois algarismos e da divisão exata por números de um algarismo, além
do reconhecimento de figuras bidimensionais pelo número de lados e pelo ângulo reto, e da planificaçã
do cone e do cubo. Os estudantes diferenciam entre os diversos sólidos, os que têm superfícies
arredondadas; localizam pontos usando coordenadas cartesianas em um referencial quadriculado;
identificam a localização ou a movimentação de objetos em representações gráficas, com base e
referencial igual ou diferente da própria posição.
Constata-se, também, que esses estudantes lidam com os algoritmos das operações aritméticas; localizam
números na reta numérica; reconhecem a escrita por extenso de números naturais e a sua composição
e decomposição em dezenas e unidades, considerando o seu valor posicional na base decimal; resolvem
problemas envolvendo a soma ou subtração de números racionais na forma decimal, constituídos pelo
mesmo número de casas decimais e por até três algarismos, e resolvem problemas envolvendo a soma de
números naturais. Esses estudantes reconhecem as características do Sistema de Numeração Decimal.
Ainda, nesse Padrão, os estudantes já demonstram conhecimentos básicos relativos à Literacia Estatística;
conseguem ler e interpretar informações elementares e explícitas em um gráfico de colunas, por meio
da leitura de valores do eixo vertical, e ler informações em tabelas de coluna única e de dupla entrada.
Identificam dados em uma lista de alternativas, utilizando-os na resolução de problemas, relacionando-os,
dessa forma, às informações apresentadas em gráficos de barras e tabelas. São capazes, ainda, de resolver
problemas envolvendo as operações, usando dados apresentados em gráficos ou tabelas, inclusive com
duas entradas.
Nesse Padrão de Desempenho, os estudantes também demonstram compreender a ação de medir um
comprimento utilizando régua numerada e estabelecer as relações entre as unidades de medida de
comprimento (metros e centímetros). Eles também estabelecem relações entre diferentes medidas de
tempo (dias e semanas, horas e minutos) e realizam cálculos simples com essas medidas; leem horas e
minutos em relógios analógicos e digitais; realizam trocas de moedas em valores monetários pequenos
e identificam cédulas que formam uma quantia de dinheiro inteira; identificam a forma ampliada de um
figura simples em uma malha quadriculada; resolvem problemas de cálculo de área com base na contagem
das unidades de uma malha quadriculada; reconhecem a quarta parte de um todo; estimam medida
de comprimento usando unidades convencionais e não convencionais, além de resolverem problemas
envolvendo operações acerca do Sistema Monetário brasileiro.
As habilidades matemáticas evidenciadas nesse Padrão são elementares para esta série e o desafio que se
apresenta é o de viabilizar condições para que os estudantes possam vencer as próximas etapas escolares.
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
(M050405EX) Sofia encontrou em um livro o molde de um cubo como representado abaixo e resolveu montá-lo.
Qual sólido Sofia montou usando esse molde?
A)
B)
C)
D)
Esse item avalia a habilidade de os estudantes identificarem u
sólido geométrico a partir de sua planificação
Para resolvê-lo, eles devem reconhecer as formas geométricas que
compõe o poliedro. Como a planificação corresponde a um poliedro,
cujas seis faces são todas quadradas, então devem observar que ela
está associada ao cubo, ou seja, aqueles que marcaram a alternativa
B, provavelmente, já desenvolveram a habilidade avaliada pelo item.
Aqueles que escolheram a alternativa A identificaram corretamente
a correspondência entre o número de faces dessa planificação e do
bloco retangular, mas cometeram um equívoco ao identificá-las como
quadrados. Por outro lado, aqueles que optaram pela alternativa
C, provavelmente, não observaram que o número de faces de uma
pirâmide quadrangular é menor do que o número de faces da
planificação dada no suporte e, além disso, não identificaram qu
quatro faces da pirâmide são triângulos. Já os que marcaram a letra
D identificaram, equivocadamente, as bases de um prisma hexagonal
como figuras poligonais de quatro lados iguais.
Como a habilidade avaliada por este item envolve essencialmente
a visualização, para seu desenvolvimento sugere-se que, durante o
processo de ensino, os estudantes tenham alguma experiência de
84
84,0% de acerto
A
B
C
D
4,8% 84,0% 1,9% 7,8%
construção de diversos sólidos a partir de suas planificações, seja
usando papel ou outros materiais, ou mesmo usando algum software.
Dessa maneira, espera-se que eles se apropriem das imagens dos
sólidos geométricos, diferenciando uma da outra por meio de suas
características, e que sejam capazes de “abrir” e/ou “fechar” os sólidos
mentlmente, o que facilita a identificação da planificação. També
é importante que eles sejam capazes de perceber as características
e propriedades das figuras bidimensionais que compõe os sólidos
geométricos.
(MEF0040PC)
Resolva a operação abaixo.
3 096 – 1 997
Qual é o resultado dessa operação?
A) 1 099
B) 1 199
C) 2 198
D) 2 901
Esse item avalia a habilidade de os estudantes
A alternativa D indica que os estudantes que a
calcularem a subtração de números naturais com
marcaram provavelmente identificaram a subtração
reserva.
apenas como retirada do maior pelo menor
Para resolvê-lo, uma das estratégias possíveis é
utilizar o algoritmo da subtração, escrevendo-o na
forma vertical, alinhando as parcelas à direita de
algarismo, independente da posição na armação
da conta, por exemplo, na ordem das unidades
efetuaram a subtração do 7 pelo 6.
modo que os algarismos de cada ordem fique
Ao final do 9º ano do Ensino Fundamental, espera
posicionados verticalmente e calculando a subtração
se que os estudantes compreendam o Sistema de
em cada uma delas. Além disso, devem saber aplicar o
Numeração Decimal e sejam capazes de utilizar
reagrupamento. Dessa forma, aqueles que marcaram
o algoritmo da subtração como estratégia para
a alternativa A, possivelmente, desenvolveram a
cálculos em seus diferentes contextos, inclusive
habilidade avaliada pelo item.
compreendendo o significado dos reagrupamentos
A opção pela alternativa B sugere que os
respondentes provavelmente não utilizaram
corretamente o algoritmo da subtração,
equivocando-se no reagrupamento da ordem das
unidades de milhar para a ordem das centenas.
Já aqueles que marcaram a alternativa C, além
de não se apropriarem do reagrupamento,
podem ter realizado uma contagem equivocada
obtendo 8 como resultado da subtração de 16
por 7. Essa operação mental pode acontecer de
forma inconsciente, apontando para a falta de
compreensão do Sistema de Numeração Decimal.
no contexto de sua aplicação.
53
53,1% de acerto
A
B
C
D
53,1% 14,7% 7,2% 23,5%
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
Observe abaixo mais alguns exemplos de itens representativos desse
padrão de desempenho.
(M050795E4) Em um dia, Marcelo foi ao mercado e comprou 1,8 kg de laranjas e 2,3 kg de maçãs.
Nesse dia, quantos quilogramas de frutas Marcelo comprou, ao todo, no mercado?
A) 4,1 kg
B) 3,1 kg
C) 1,8 kg
D) 0,5 kg
Esse item avalia a habilidade de os estudantes resolverem problemas
envolvendo a adição de números racionais
84
84,5% de acerto
A
B
C
D
84,5% 9,8% 2,3% 1,7%
(MEF0104PC) Resolva
a operação abaixo.
136 ÷ 4
Qual é o resultado dessa operação?
A) 50
B) 34
C) 31
D) 26
Esse item avalia a habilidade de os estudantes efetuarem a divisão
entre números naturais sem resto.
82
82,1% de acerto
A
B
C
D
4,2% 82,1% 6,7% 5,7%
Básico
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
500
de 225 a 275 pontos
Os estudantes que se encontram nesse Padrão de Desempenho demonstram já terem começado um
processo de sistematização e domínio das habilidades consideradas básicas e essenciais ao período de
escolarização em que se encontram. No conjunto dos números naturais esses estudantes identificam
números em um intervalo dado; reconhecem a lei de formação de uma sequência; resolvem uma divisão
exata por números de até dois algarismos e uma multiplicação cujos fatores também são números de
até dois algarismos; resolvem problemas utilizando a multiplicação, reconhecendo que um número não
se altera ao multiplicá-lo por um; resolvem problemas envolvendo várias operações; resolvem problemas
de soma, envolvendo combinações, e de multiplicação, envolvendo configuração retangular; assim como,
resolvem problemas de contagem em uma disposição retangular envolvendo mais de uma operação.
Eles, também, reconhecem a representação numérica de uma fração com apoio de representação gráfica;
comparam números racionais na forma decimal com diferentes partes inteiras; calculam porcentagens;
localizam números racionais (positivos e negativos), na forma decimal, na reta numérica e resolvem
problemas de soma ou subtração de números decimais encontrados no Sistema Monetário brasileiro.
Nesse Padrão demonstram uma compreensão mais ampla do Sistema de Numeração Decimal,
reconhecendo a composição e decomposição na escrita decimal envolvendo casos mais complexos;
calculam expressão numérica envolvendo soma e subtração com uso de parênteses e colchetes; calculam
o resultado de uma divisão por um número de dois algarismos, inclusive com resto; reconhecem a
modificação sofrida no valor de um número quando um algarismo é alterado, além de resolver problemas
envolvendo subtração de números decimais com o mesmo número de casas.
No Padrão Básico, os estudantes do 9°ano também conseguem estimar comprimento utilizando unidade
de medida não convencional e calcular a medida do perímetro com ou sem apoio da malha quadriculada.
Também realizam conversões entre unidades de medida de comprimento (m/km), massa (Kg/g), tempo
(mês/trimestre/ano, hora/minuto, dias/ano), temperatura e capacidade (mL/L). Esses estudantes leem
horas em relógios de ponteiros em situações mais gerais (por exemplo, 8h50min) e atribuem significado
para o metro quadrado. Eles resolvem problemas incluindo o Sistema Monetário brasileiro, além de
comparar áreas de figuras poligonais em malhas quadriculadas
No Campo Geométrico, os estudantes identificam algumas características de quadriláteros relativas aos
lados e ângulos; reconhecem alguns polígonos (triângulos, quadriláteros, pentágonos, hexágonos) e
círculos; reconhecem que a medida do perímetro de um polígono, em uma malha quadriculada, dobra
ou se reduz à metade, quando os lados dobram ou são reduzidos à metade; identificam propriedades
comuns e diferenças entre sólidos geométricos através do número de faces; associam uma trajetória à sua
representação textual e identificam a localização ou movimentação de objeto em representações gráficas
situadas em referencial diferente ao do estudante.
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
Nesse Padrão, percebe-se, ainda, que esses estudantes localizam informações em gráficos de colunas
duplas; resolvem problemas que envolvem a interpretação de dados apresentados em gráficos de barras
ou em tabelas; leem gráficos de setores; identificam gráficos de colunas que corresponde a uma tabe
com números positivos e negativos; localizam dados em tabelas de múltiplas entradas; reconhecem
o gráfico de colunas correspondente a dados apresentados de forma textual; identificam o gráfico
colunas correspondente a um gráfico de setores; leem tabelas de dupla entrada e reconhecem o gráfico de
colunas correspondente, mesmo quando há variáveis representadas.
(M090149B1) O
sólido abaixo é composto por cubos de 1m3 de volume.
Qual é a medida do volume desse sólido?
A) 17 m3
B) 9 m3
C) 8 m3
D) 4 m3
Esse item avalia a habilidade de os estudantes resolverem problemas
envolvendo o volume de um sólido geométrico.
Para resolvê-lo, eles devem calcular o volume por meio da contagem
dos cubinhos que compõe o sólido. Para tal, devem se apropriar
da informação dada no enunciado de que cada cubo possui 1m³
de volume, dessa forma, 8 cubinhos possuem 8 m³ de volume.
Logo, os estudantes que optaram pela alternativa C, possivelmente,
desenvolveram a habilidade avaliada pelo item.
A opção pelas demais alternativas apresenta um possível
desconhecimento do procedimento para o cálculo do volume. Os
estudantes que marcaram a alternativa B, provavelmente, contaram o
cubo que liga a coluna vertical à horizontal duas vezes. Já aqueles que
assinalaram a alternativa D, supostamente, calcularam os cubos que
compõem a coluna horizontal do sólido.
Medir é uma ação essencial no cotidiano, na Matemática e nas
demais ciências em geral, portanto é evidente que os estudantes
devam compreender não somente como medir, mas também o que
significa medir. Medir significa comparar uma grandeza com um
unidade de referência de mesma espécie. No caso do presente item,
medir o volume do sólido significa dizer quantos cubinhos de 1 m³ de
volume o compõe, e a estratégia natural para fazer essa medição é a
contagem dos cubinhos.
No decorrer do processo de ensino, os estudantes devem
compreender a necessidade dos instrumentos e das unidades de
medida convencionais, com os quais é possível associar um número
e uma unidade para a medida de uma determinada grandeza. No
que se refere à grandeza volume, devem também se apropriar de
estratégias para medi-la sem a contagem.
71
71,6% de acerto
A
B
C
D
8,8% 10,6% 71,6% 7,4%
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
(M050816A9)
Observe a reta numérica abaixo. Essa reta está dividida em segmentos de mesma medida.
R
30
30,5
31
S
33
33,5
Nessa reta, quais números correspondem aos pontos R e S?
A) 31,5 e 34.
B) 32 e 34.
C) 32 e 34,5.
D) 32,5 e 34,5.
Esse item avalia a habilidade de os estudantes localizarem números
racionais, em sua representação decimal, na reta numérica.
Para resolvê-lo, eles devem, primeiramente, perceber que a reta
numérica foi subdividida em intervalos de comprimento igual a 0,5.
Em seguida, é preciso reconhecer a ordenação dos números racionais
na forma decimal. Nesse caso, o número 32, representado pelo ponto
R se encontra entre os números 31 e 33, a duas graduações à direita
do 31 ou duas graduações à esquerda do 33. De forma análoga, o
ponto representado pela letra S é representado pelo número 34,5,
pois está duas graduações à direita do 33,5. Portanto, os estudantes
que optaram pela alternativa C, provavelmente, desenvolveram a
habilidade avaliada pelo item.
A seleção das demais alternativas sugere que os respondentes,
possivelmente, não sabem ordenar números racionais na forma
decimal ou não reconhecem a reta numérica.
Ao final do Ensino Fundamental, espera-se que os estudantes sejam
capazes de compreender a correspondência biunívoca existente
entre os números racionais e a sua posição na reta numérica. Como
no Ensino Médio ocorre uma retomada do estudo dos conjuntos
numéricos como pré-requisito para o estudo das funções, então é
esperado que a habilidade avaliada por este item esteja consolidada.
Deve-se levar em consideração que a extensão desta habilidade para
a localização dos números reais requer que os estudantes saibam
reconhecer as diferentes representações de um número racional e
também estimar valores aproximados de radicais.
68
68,5% de acerto
A
B
C
D
8,4% 8,0% 68,5% 13,5%
Observe abaixo mais alguns exemplos de itens representativos desse
padrão de desempenho.
(M070221B1) André
saiu de Beijim e virou à segunda estrada à esquerda. Observe o mapa abaixo.
Fl
or
o
d
in
L
es
as
el
an
C
M
on
te
s
Beijim
Para qual cidade ele foi?
A) Canelas.
B) Flores.
C) Lindo.
D) Montes.
Esse item avalia a habilidade de os estudantes resolverem problema
envolvendo a localização de objetos em mapas.
51
51,9% de acerto
A
B
C
D
29,5% 7,3% 9,5% 51,9%
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
A tabela abaixo informa a quantidade de pessoas que acessaram uma página da internet
durante uma semana.
(M090595ES)
Número de acessos a uma página da internet
Dia da semana
Número de acessos
Segunda-feira
Terça-feira
Quarta-feira
Quinta-feira
Sexta-feira
100
75
50
100
125
O gráfico que melhor representa os dados dessa tabela é
A)
B)
Número de acessos a uma página
da Internet
140
120
120
100
100
Número de
acessos
Número de
acessos
140
80
60
80
60
40
40
20
20
0
Número de acessos a uma página
da Internet
0
Seg
Ter
Qua
Qui
Seg
Sex
Dia da semana
C)
Número de acessos a uma página
da Internet
D)
140
120
120
100
100
80
60
Sex
Número de acessos a uma página
da Internet
80
60
40
40
20
20
0
0
Seg
Ter
Qua
Qui
Sex
Dia da semana
Esse item avalia a habilidade de os estudantes relacionarem
as informações apresentadas em tabelas aos gráficos que as
representam.
Qui
Qua
Dia da semana
Número de
acessos
Número de
acessos
140
Ter
Seg
Ter
Qui
Qua
Sex
Dia da semana
87
87,0% de acerto
A
B
C
D
87,0% 3,9% 2,3% 5,3%
Proficiente
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
500
de 275 a 325 pontos
Nesse Padrão amplia-se o leque de habilidades relativas ao Campo Numérico e ao Campo Algébrico,
notando ainda, o desenvolvimento das noções algébricas.
No conjunto dos números racionais esses estudantes identificam mais de uma forma de representar
numericamente uma mesma fração; transformam fração em porcentagem e vice-versa; localizam números
decimais negativos na reta numérica; estabelecem a relação entre frações próprias e impróprias e as suas
representações na forma decimal; resolvem problemas de soma ou subtração de números decimais na
forma do Sistema Monetário brasileiro em situações mais complexas e identificam fração como parte de
um todo, sem apoio da figura. Resolvem problemas que envolvem proporcionalidade envolvendo mais
de uma operação; problemas utilizando multiplicação e divisão em situação combinatória; problemas
de contagem utilizando o princípio multiplicativo. Eles, também, efetuam cálculos de números naturais
que requer o reconhecimento do algoritmo da divisão inexata; identificam a localização aproximada de
números inteiros não ordenados, em uma reta em que a escala não é unitária. Esses estudantes, também,
ordenam e comparam números inteiros negativos; identificam um número natural não informado na reta
numérica e calculam expressões numéricas com números inteiros.
No Campo Algébrico, esses estudantes identificam equações e sistemas de equações de primeiro grau
que permitem resolver um problema; calculam o valor numérico de uma expressão algébrica, incluindo
potenciação e identificam a equação do 1º grau adequada à solução de um problema
No Campo Geométrico, os estudantes identificam elementos de figuras tridimensionais; resolve
problemas envolvendo as propriedades dos polígonos regulares inscritos (hexágono), para calcular o seu
perímetro; reconhecem um quadrado fora da posição usual; avaliam distâncias horizontais e verticais em
um croqui, usando uma escala gráfica dada por uma malha quadriculada, reconhecendo o paralelismo;
contam blocos em um empilhamento; sabem que em uma figura obtida por ampliação ou redução
os ângulos não se alteram; identificam a localização de um objeto requerendo o uso das definiçõe
relacionadas ao conceito de lateralidade, tendo por referência pontos com posição oposta a do observador
e envolvendo combinações. Esses estudantes também reconhecem diferentes planificações de um cubo;
identificam as posições dos lados de quadriláteros (paralelismo); relacionam poliedros e corpos redondos
às suas planificações além de localizarem pontos no plano cartesiano
Os estudantes, nesse Padrão, compreendem o significado da palavra perímetro, realizam conversão e
soma de medidas de comprimento e massa (m/km, g/kg), resolvem problemas de cálculo de área com base
em informações sobre ângulos de uma figura e calculam a medida do volume por meio da contagem de
blocos. Percebe-se, ainda, que esses estudantes reconhecem o gráfico de linhas correspondente a uma
sequência de valores ao longo do tempo (com valores positivos e negativos).
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
(M090772ES) Após a secagem de um determinado tipo de grão, um produtor verificou que houve uma redução
em quilogramas desse grão na razão de 3 para 1. Esse produtor colheu 327 kg desse grão.
Mantendo essa proporção, quantos quilogramas esse produtor terá após essa secagem?
A) 981 kg
B) 327 kg
C) 324 kg
D) 109 kg
Esse item avalia a habilidade de os estudantes resolverem problemas
envolvendo variação proporcional direta entre grandezas.
Para resolvê-lo, eles devem se apropriar da informação presente
no enunciado que, durante o processo de secagem, ocorre uma
redução no grão a uma razão de 3 kg para 1 kg. Eles podem utilizar
uma regra de três para modelar e resolver o problema, separando
em uma coluna a quantidade de grãos colhidos (que passarão por
essa secagem) e em outra coluna a quantidade do produto após o
processo de secagem.
Como as grandezas são diretamente proporcionais, devem perceber
que a quantidade de grãos (em quilogramas) após o processo de
secagem pode ser encontrado por meio da resolução da igualdade:
Outro procedimento mais direto é perceber que existe uma redução
de
da quantidade de grãos (em quilogramas) durante o processo
de secagem. Logo, os estudantes poderiam realizar de forma direta o
cálculo 327 x
= 109 . Os estudantes que marcaram a alternativa D
demonstram ter desenvolvido a habilidade avaliada.
Aqueles que marcaram a opção A, provavelmente, compreenderam
de forma equivocada que, ao invés de ocorrer uma redução da
quantidade de grãos no processo, ocorreu um aumento, verificando
que a quantidade de grãos triplicou após a secagem.
A escolha das alternativas B ou C indica que esses estudantes,
possivelmente, não se apropriaram da relação de proporcionalidade
direta implícita no enunciado do item e apenas mantiveram a mesma
quantidade de grãos após a secagem (alternativa B) ou realizaram
apenas a subtração 327 – 3, encontrando como resposta 324 kg
(alternativa C).
36
36,1% de acerto
A
B
C
D
19,2% 17,0% 25,0% 36,1%
Constata-se, ao analisar esse item, que os estudantes só irão
desenvolver essa habilidade quando conseguirem compreender
a relação existente entre as quantidades envolvidas nos diversos
contextos e forem capazes de entender a operação aritmética que
subjaz a manipulação dessas quantidades. Para isso, é preciso que
se perceba a forma como eles manipulam as quantidades extensivas1
e intensivas, bem como quantidades contínuas e descontínuas2 . A
partir dessa observação, é necessário fazer intervenções pedagógicas
pontuais, criando situações-problema que permitam intervir na forma
como o pensamento aritmético desses estudantes é desenvolvido.
1. Entendemos por quantidade extensiva aquela relativa à comparação de duas
quantidades de mesma natureza e na lógica parte-todo¬¬ e, por quantidade intensiva, a
quantidade medida através da comparação entre duas quantidades diferentes.
2. Segundo salienta Nunes (2009, p.120), as quantidades descontínuas são aquelas em
que as unidades são objetos distintos, exemplo: no caso de “botões”, a unidade a qual
nos referimos quando dizemos “3 botões” é uma unidade natural, pois um botão também
é um objeto. Nesse contexto, concluímos que, no caso das quantidades contínuas, as
diferentes unidades que compõem a quantidade não são percebidas separadamente.
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
(M090065ES) O
valor numérico da expressão
A) 1
B)
8
3
C)
11
3
x2 – 2y
, para x = 3 e y = – 1, é
x
D) 5
Esse item avalia a habilidade de os estudantes calcularem o valor
numérico de uma expressão algébrica.
Para resolvê-lo, inicialmente, os estudantes devem substituir os
valores atribuídos a x e y na expressão algébrica, tornando-a
uma expressão numérica:
2
. Para continuar a resolução
desse problema, o estudante deve se atentar para a Ordem das
Operações Aritméticas ou Algébricas3, encontrando como resposta
. Os estudantes que assinalaram a alternativa C, possivelmente,
desenvolveram a habilidade avaliada pelo item.
Aqueles que optaram pela alternativa B realizam a substituição dos
valores de x e y na expressão corretamente, porém associaram
a potência como uma multiplicação da base pelo expoente,
encontrando:
+
. Os estudantes que optaram pelas
alternativas A ou D, possivelmente, realizaram uma simplificação
do termo x2 no numerador e o termo x no denominador, ainda na
parte no numerador e o termo x no denominador, ainda na parte
algébrica, fazendo
(alternativa D) ou
(alternativa A).
A compreensão de uma expressão algébrica requer que os
estudantes se apropriem das operações aritméticas e de suas
propriedades. No caso desse item, por exemplo, eles devem perceber
que a simplificação
está incorreta, pois não atende à
propriedade distributiva. Cabe ressaltar que as identidades algébricas
e as afirmativas sobre expressões algébricas podem ser verificada
na própria substituição, como é o caso do presente item, no qual
e
para x = 3 e y = -1.
O estudo de problemas que podem ocorrer no cálculo do valor
numérico de uma expressão algébrica deve supor, a não ser em casos
3. Em matemática, ordem de operações refere-se à ordem pela qual devem ser realizadas
as operações.
35
35,2% de acerto
A
B
C
D
21,7% 28,0% 35,2% 13,5%
óbvios, que os estudantes já saibam resolver equações e inequações
simples. Por exemplo, para saber que a substituição
possível em
não é
eles já devem saber resolver a equação 2x - 1 = 0.4
Do ponto de vista operacional, o cálculo do valor numérico de uma
expressão não apresenta nada de novo, pois é equivalente a efetuar
operações numéricas. Assim, ao trabalhar com substituição, devese mostrar para que ela serve e não transformá-la, apenas, em
um exercício mecânico de cálculo numérico. A parte estritamente
numérica – isto é, efetuar as operações indicadas após realizada a
substituição – pode servir para o professor se certificar de que os
estudantes têm as habilidades manipulativas necessárias.
4. Adaptação das Orientações Pedagógicas de Matemática – Ensino Fundamental – 6º ao
9º ano do Centro de Referência Virtual do Professor – SEE/MG. Disponível em: <http://crv.
educacao.mg.gov.br/> Último acesso em dez. 2013.
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
Abaixo, seguem outros exemplos de itens característicos desse
Padrão de Desempenho.
(M090695ES) Carol e Alexandre têm, juntos, 1 000 reais, sendo que o dobro do valor de Alexandre corresponde
ao triplo do valor de Carol.
Chamando o valor de Carol de C e o valor de Alexandre de A, qual sistema de equações permite determinar
esses dois valores?
A)
B)
C)
D)
'
C + A = 1 000
2C = 3A
'
C + A = 1 000
3C = 2A
'
2C + 3A = 1 000
2C = 3A
'
2C + 3A = 1 000
3C = 2A
Esse item avalia a habilidade de os estudantes identificarem um
sistema de equações do 1° grau que expressa um problema.
48
48,7% de acerto
A
B
C
D
24,8% 48,7% 14,4% 10,8%
observou que 1 de suas blusas são listradas.
4
O percentual de blusas listradas que Rute tem é de
(M050688A9) Rute
A) 4%
B) 12%
C) 25%
D) 50%
Esse item avalia a habilidade de os estudantes relacionarem a
representação fracionária de um número racional com a sua
representação percentual.
32
32,7% de acerto
A
B
C
D
47,0% 16,6% 32,7% 2,3%
Avançado
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
500
acima de 325 pontos
As habilidades características desse Padrão de Desempenho evidenciam uma maior expansão dos Campos
Numérico e Geométrico. Os estudantes demonstram compreender o significado de números racionais em
situações mais complexas, que exigem deles uma maior abstração em relação a esse conhecimento. Eles
reconhecem as diferentes representações decimais de um número fracionário, identificando suas ordens
(décimos, centésimos e milésimos); calculam expressões numéricas com números decimais positivos e
negativos; localizam frações na reta numérica; reconhecem o valor posicional de um algarismo decimal e
a nomenclatura das ordens; efetuam adição de frações com denominadores diferentes; efetuam cálculos
de divisão com números racionais nas formas fracionária e decimal simultaneamente, calculam expressões
com numerais na forma decimal com quantidades de casas diferentes, além de calcular o resultado de
expressões envolvendo, além das quatro operações, números decimais (positivos e negativos, potências e
raízes); efetuam cálculos de raízes quadradas e identificam o intervalo numérico em que se encontra uma
raiz quadrada não exata; efetuam arredondamento de decimais; resolvem problemas envolvendo variação
proporcional entre mais de duas grandezas além de resolverem problemas envolvendo porcentagens
diversas e suas representações na forma fracionária (incluindo noção de juros simples e lucro).
Nesse Padrão, os estudantes demonstram resolver problemas com números inteiros positivos e negativos
não explícitos com sinais e conseguem obter a média aritmética de um conjunto de valores. Embora o
cálculo da média aritmética requeira um conjunto de habilidades já desenvolvidas pelos estudantes em
anos escolares anteriores, que utilizam, na prática, essa ideia para compor a nota bimestral ou em outros
contextos extraescolares, o conceito básico de estatística, combinado com o raciocínio numérico, só é
desempenhado pelos estudantes nesse Padrão da Escala.
Percebe-se, ainda, um salto cognitivo em relação ao estudo da Álgebra, pois esses estudantes identificam
a inequação do primeiro grau adequada para a solução de um problema; resolvem problemas de adição
e multiplicação; resolvem problemas envolvendo a identificação de um sistema de equações do primeiro
grau com duas incógnitas; resolvem problemas envolvendo o cálculo numérico de uma expressão algébrica
em sua forma fracionária; resolvem problemas envolvendo equação do 2° grau e sistema de equações do
1° grau. Resolvem, também, problemas envolvendo juros simples.
No Campo Geométrico, há um avanço significativo no desenvolvimento das habilidades. Os estudantes
resolvem problemas envolvendo a lei angular de Tales; o teorema de Pitágoras e as demaisrelações
métricas no triângulo retângulo; propriedades dos polígonos regulares, inclusive por meio de equação
do primeiro grau. Eles também aplicam as propriedades de semelhança de triângulos na resolução
de problemas; reconhecem que a área de um retângulo quadruplica quando seus lados dobram;
resolvem problemas envolvendo círculos concêntricos; resolvem problemas utilizando propriedades de
triângulos e quadriláteros; identificam propriedades comuns e diferenças entre figuras bidimensionais
tridimensionais, relacionando estas às suas planificações, além de identificar o sólido que correspond
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
a uma planificação dada, reconhecem a proporcionalidade entre comprimentos em figuras relacionada
por ampliação ou redução; calculam ângulos centrais em uma circunferência dividida em partes iguais.
Esses estudantes também localizam pontos em um referencial cartesiano; classificam ângulos em agudos,
retos ou obtusos de acordo com suas medidas em graus; calculam ampliação, redução ou conservação da
medida de ângulos informada inicialmente, lados e áreas de figuras planas; além de realizarem operações,
estabelecendo relações e utilizando os elementos de um círculo ou circunferência (raio, corda, diâmetro)
e solucionam problemas em que a razão de semelhança entre polígonos é dada, por exemplo, em
representações gráficas envolvendo o uso de escalas
Os estudantes nesse Padrão calculam a medida do perímetro de polígonos sem o apoio de malhas
quadriculadas e calculam a área de figuras simples (triângulo, paralelogramo, retângulo, trapézio). Em
relação ao conceito de volume, esses estudantes conseguem determinar a medida do volume do cubo
e do paralelepípedo pela multiplicação das medidas de suas arestas e realizam conversões entre metro
cúbico e litro.
No Padrão Avançado da Escala, os estudantes utilizam o raciocínio matemático de forma mais complexa,
conseguindo identificar e relacionar os dados apresentados em diferentes gráficos e tabelas par
resolver problemas ou fazer inferências. Analisam gráficos de colunas representando diversas variáveis,
comparando seu crescimento e leem informações fornecidas em gráficos envolvendo regiões do plano
cartesiano.
Para plantar uma flor, Vanessa comprou um vaso com formato de cubo, cuja aresta interna
mede 8 cm, e terra suficiente para encher esse vaso.
Qual é a quantidade de terra, em cm³, necessária para encher completamente esse vaso?
(M080135E4)
A) 24
B) 64
C) 72
D) 512
Esse item avalia a habilidade de os estudantes
largura e comprimento, os estudantes precisam já
resolverem problemas envolvendo o volume de um
ter se apropriado do significado de capacidade po
cubo.
meio de experiências com materiais manipuláveis.
Em etapas iniciais de escolarização, os estudantes
Para resolvê-lo, eles devem, primeiramente, se
podem usar esses materiais (cubinhos, água, areia,
apropriar da informação de que o vaso tem o
formato de um cubo. Em seguida, para determinar
a quantidade de terra necessária para encher
completamente esse vaso, eles devem calcular seu
volume, o que pode ser feito por meio do produto de
suas dimensões internas (8 cm x 8 cm x 8 cm = 512
arroz, etc.) para preencher recipientes e medir a
quantidade utilizada. Em etapas subsequentes,
eles devem perceber que na representação de um
tipo especial de recipiente (prisma retangular com
dimensões a, b, c), como mostra o prisma abaixo,
cm³) ou com o uso da fórmula
.Logo, os estudantes que optaram pela alternativa D,
possivelmente, desenvolveram a habilidade avaliada
pelo item.
Aqueles que assinalaram a alternativa A,
provavelmente, não se apropriaram do conceito
de volume e realizaram a soma das dimensões
(comprimento, largura e altura) ao invés do produto.
Cabe ressaltar que os estudantes também podem
ter escolhido esse distrator por causa de um erro
durante a manipulação aritmética da fórmula, ao
associar a potência 8 como a multiplicação 8 x 3,
3
encontrando como resposta 24cm3. Aqueles que
optaram pela alternativa B, possivelmente, não se
apropriaram do enunciado do item e realizaram
o cálculo da área do quadrado, encontrando 64.
Os estudantes que marcaram a alternativa C,
provavelmente, realizaram o cálculo da área da base
do cubo fazendo
, mas, ao invés
de multiplicarem esse valor com a altura, realizaram
uma soma, encontrando:
.
Para lançar os fundamentos para a compreensão de
como calcular o volume dos prismas retangulares,
bem como entender a relação existente entre altura,
a base (uma camada) pode ser preenchida por (a x
b) cubos de 1 unidade cúbica de medida, para então
reconhecer que há c dessas camadas na estrutura
vertical. Portanto, o volume do prisma retangular
pode ser dado por (a x b) x c. (Confrey et al, 2012)5.
14
14,8% de acerto
A
B
C
D
44,6% 28,8% 10,5% 14,8%
5. Confrey, J., Nguyen, K. H., Lee, K., Panorkou, N., Corley, A.
K., and Maloney, A. P. (2012). Turn-On Common Core Math:
Learning Trajectories for the Common Core State Standards for
Mathematics. Disponível em: <www.turnonccmath.net> . Último
acesso em nov.2013.
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
(M080068E4)
Resolva a operação abaixo.
5 2 1
+ +
4 3 2
Qual é o resultado dessa operação?
29
12
B) 21
12
C) 8
9
D) 8
24
A)
Esse item avalia a habilidade de os estudantes efetuarem cálculo entre
números racionais representados na forma fracionária.
Para resolvê-lo, uma estratégia possível é calcular o mínimo múltiplo
comum (M.M.C) dos denominadores das frações (4, 3, 2), encontrando
12. Em seguida, deve-se dividir o valor encontrado pelo denominador
de cada fração e multiplicar o valor encontrado pelos respectivos
, encontrando como
numeradores, fazendo
resultado a fração
. Os estudantes que assinalaram a alternativa A
demonstraram ter desenvolvido a habilidade avaliada pelo item.
Aqueles que optaram pela alternativa B, possivelmente, calcularam
corretamente o mínimo múltiplo comum dessas frações e realizaram
a divisão desse valor pelo denominador de cada fração, mas ao
invés de multiplicar esse valor pelo numerador, realizam a soma,
. Os estudantes que assinalaram
encontrando
a alternativa C, provavelmente, apenas somaram os numeradores e
os denominadores das frações, encontrando
. Já os que optaram
pela alternativa D, possivelmente, somaram o numerador dessas
frações (5 + 2 + 1 = 8) e multiplicaram os denominadores (4x3x2=24),
encontrando a fração
.
O aspecto mais delicado no estudo dos números racionais é o de se
dar um significado às “regras” operatórias de adição, multiplicação
e, principalmente, a divisão. Como se sabe, os números inteiros são
racionais particulares. As “regras” operatórias para o racionais devem
ser tais que, se aplicadas aos inteiros, preservam os resultados e
as propriedades já conhecidas. Essa justificativa para as diferenças
notórias entre as operações com inteiros e com racionais não
inteiros, ultrapassa o nível de compreensão dos alunos do Ensino
12
12,1% de acerto
A
B
C
D
12,1% 6,2% 74,0% 6,3%
Fundamental. No entanto, ela deve ser explicitada para servir de
referência na busca de significados para estudantes desse nível
Sugere-se que as operações com frações sejam iniciadas pela adição
de frações com mesmo denominador. Aqui também é recomendável
a utilização de material concreto. Para a adição de frações com
denominadores diferentes, sugere-se que sejam apresentados
exemplos para mostrar que a mera adição dos numeradores entre si
e dos denominadores entre si não funciona. Por exemplo, eles devem
compreender que
é maior que
não é igual a
, porque
é igual a
,e
. Logo, o recurso é transformar essas frações em frações
equivalentes de mesmo denominador. Para essa transformação, é
necessário que os estudantes percebam a conveniência da simplificação
das frações e do uso do mínimo múltiplo comum, para se evitar o
trabalho com números “muito grandes”. O trabalho com a subtração
deve ser feito de forma análoga ao da adição6.
6. Adaptação das Orientações Pedagógicas de Matemática – Ensino Fundamental – 6º ao
9º ano do Centro de Referência Virtual do Professor – SEE/MG. Disponível em: <http://crv.
educacao.mg.gov.br/> Último acesso em jan. 2014.
Observe abaixo outros exemplos de itens característicos desse padrão
de desempenho.
(M090186C2) Um portão retangular com barras de metal teve sua estrutura reforçada por barras metálicas
mais resistentes, formando um triângulo retângulo, conforme representado no desenho abaixo.
P
N
M
H
1,2 m
3,5 m
O comprimento da barra PM, em metros, é, aproximadamente,
A) 2,04
B) 3,70
C) 4,05
D) 4,70
Matemática - 9º ano do Ensino Fundamental | SAEGO 2013
Esse item avalia a habilidade de os estudantes resolverem problemas
envolvendo relações métricas no triângulo retângulo.
21
21,2% de acerto
A
B
C
D
11,5% 30,0% 21,2% 35,5%
(M090244E4) Na
circunferência de centro O abaixo foram traçados alguns segmentos.
O segmento que representa um raio dessa circunferência é
A) RP.
B) OS.
C) MS.
D) PS.
Esse item avalia a habilidade de os estudantes reconhecerem a
circunferência, seus elementos e algumas de suas relações.
43
43,5% de acerto
A
B
C
D
40,9% 43,5% 9,8% 4,7%