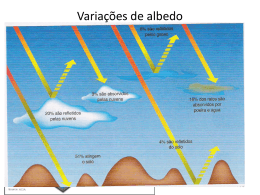
Hidrologia Urbana
Precipitação
RODRIGO F. JUNQUEIRA
FEITEP
Precipitação
 Definição: água da atmosfera depositada na
superfície terrestre.
 Formas: chuvas; granizo; neve; orvalho; neblina;
geada.
 Variabilidade temporal e espacial.
Precipitação
Mecanismo de formação: massa de ar úmido se eleva,
a temperatura diminui, mais vapor se condensa, gotas
crescem e se precipitam.
Do ponto de vista do hidrólogo a chuva tem três
mecanismos fundamentais de formação:
• chuva frontais ou ciclônicas;
• chuvas orográficas;
• chuvas convectivas térmicas.
Precipitação
Precipitação OROGRÁFICA
Precipitação CONVECTIVA
Precipitação FRONTAL
Medição de chuva
•
Benedetto Castelli, século XVII
• Quanto deve aumentar o nível da água de um lago
com a chuva?
Medição de chuva
Pluviômetros:
Pluviômetro
Fonte : Sabesp
Pluviômetro
Precipitação:
Medida com :
• Pluviômetros – leitura diária às 7 horas;
• Pluviógrafos.
Estação Pluviográfica
Estação Pluviográfica
Estação
Pluviográfica com
Telemetria
Fonte : Sabesp
Pluviógrafo
Pluviógrafo
Fonte : Sabesp
Precipitação:
Precipitação:
Radar Meteorológico
Estimativa por Satélite
• Estimativas baseadas em temperatura de brilho do
topo de nuvem (Lei de Planck):
2h c2
1
B(T)  5  hc / kT

e
1
• Quanto mais quente a nuvem “parece”, mais água
ela contém.
Testes Preliminares
90
Precipitação diária (mm)
80
Chuva média interpolada dos postos
70
Chuva média do TRMM
60
50
40
30
20
10
0
1/1/1998
2/3/1998
1/5/1998
30/6/1998
29/8/1998
28/10/1998
27/12/1998
Testes Preliminares
50
Chuva média interpolada dos postos
45
Precipitação diária (mm)
35
Diferença nas
magnitudes
Chuva média do TRMM
40
Satélite “atrasa”
30
25
Satélite “adianta”
20
15
10
Estiagem bem
representada
5
0
4/6/1998
4/7/1998
3/8/1998
2/9/1998
2/10/1998
1/11/1998
Resumo medição de chuvas
•
Pluviômetros
• Pluviógrafos
• Radar
• Satélite
Grandezas características
da precipitação
• Altura ou lâmina de chuva – medida normalmente em
milímetros
• 1 mm de chuva = 1 litro de água distribuído em 1 m2
• Intensidade da chuva é a razão entre a altura
precipitada e o tempo de duração da chuva [mm h-1].
• Grandezas:
– Duração
– Intensidade
– Freqüência
Exemplo de Registro de Chuva
Tempo Chuva
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
0
0
0
3
0
4
8
12
5
9
7
7
5
1
0
0
0
0
0
0
0
0
0
0
0
Duração da Chuva
• Tempo transcorrido entre o início e o fim do evento
chuvoso.
Duração da Chuva
• Tempo transcorrido entre o início e o fim do evento
chuvoso.
Início 03:00
Fim: 13:00
Duração = 10 horas
Chuva Acumulada
Tempo Chuva
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
0
0
0
3
0
4
8
12
5
9
7
7
5
1
0
0
0
0
0
0
0
0
0
0
0
Chuva Acumulada
0
0
0
3
3
7
15
27
32
41
48
55
60
61
61
61
61
61
61
61
61
61
61
61
61
Intensidade média
• Total precipitado = 61 mm
• Duração da chuva = 10 horas
• Intensidade média = 6,1 mm/hora
• Intensidade máxima = 12 mm/hora entre 6 e 7 horas
• Intensidade média do dia = 61/24 = 2,5 mm/hora
Freqüência
• Chuvas fracas são mais freqüentes
• Chuvas intensas são mais raras
• Por exemplo:
− Todos os anos ocorrem alguns eventos de 10 mm
em 1 dia em Porto Alegre.
− Chuvas de 180 mm em 1 dia ocorrem uma vez a
cada 10 ou 20 anos, em média.
Série de dados de chuva de um posto
pluviométrico na Região Sul
Bloco
Freqüência
P = zero
P < 10 mm
10 < P < 20 mm
20 < P < 30 mm
30 < P < 40 mm
40 < P < 50 mm
50 < P < 60 mm
60 < P < 70 mm
70 < P < 80 mm
80 < P < 90 mm
90 < P < 100 mm
100 < P < 110 mm
110 < P < 120 mm
120 < P < 130 mm
130 < P < 140 mm
140 < P < 150 mm
150 < P < 160 mm
160 < P < 170 mm
170 < P < 180 mm
180 < P < 190 mm
190 < P < 200 mm
P < 200 mm
5597
1464
459
289
177
111
66
38
28
20
8
7
2
5
2
1
1
1
2
1
0
0
Total
8279
Freqüência
Chuva média anual
Chuvas anuais
• Distribuição das chuvas se aproxima de uma
distribuição normal (exceto em regiões áridas).
• Distribuição normal tabelada para
Z = (x-)/
• Conhecendo a média e o desvio padrão das chuvas
anuais é possível associar uma chuva a uma
probabilidade.
Chuvas anuais em Blumenau - SC
Ano
Chuva (mm)
1945
1352
1946
1829
1947
1516
1948
1493
1949
1301
1950
1403
1951
1230
1952
1322
1953
1290
1954
1652
1955
1290
1956
1266
1957
1941
1958
1844
Chuva média mensal
Em Porto Alegre de 1961 a 1990
Chuvas médias mensais
Belém
Cuiabá
Porto Alegre
Florianópolis
Chuvas médias mensais
Porto Alegre
Cuiabá
Chuvas intensas
• As chuvas intensas são as causas das cheias e as
cheias são causas de grandes prejuízos quando os
rios transbordam e inundam casas, ruas, estradas,
escolas, podendo destruir plantações, edifícios, pontes
etc. e interrompendo o tráfego.
• As cheias também podem trazer sérios prejuízos à
saúde pública ao disseminar doenças de veiculação
hídrica.
Chuvas intensas
• Por estes motivos existe o interesse pelo
conhecimento detalhado de chuvas máximas no
projeto de estruturas hidráulicas como bueiros,
pontes, canais e vertedores.
• O problema da análise de freqüência de chuvas
máximas é calcular a precipitação P que atinge uma
área A em uma duração D com uma dada
probabilidade de ocorrência em um ano qualquer. A
forma de relacionar quase todas estas variáveis é a
curva de Intensidade – Duração – Freqüência (curva
IDF).
Chuvas intensas
• Obtida por análise estatística de séries longas de dados de
um pluviógrafo (mais de 15 anos, pelo menos).
• Seleção das maiores chuvas de uma duração escolhida (por
exemplo 15 minutos) em cada ano da série de dados.
• Ajuste de uma distribuição de freqüências que melhor
represente a distribuição dos valores observados.
• Procedimento repetido para diferentes durações de chuva (5
minutos; 10 minutos; 1 hora; 12 horas; 24 horas; 2 dias; 5
dias).
• Resultados resumidos na forma de um gráfico, ou equação,
com a relação das três variáveis: Intensidade, Duração e
Freqüência (ou tempo de retorno).
Chuva máxima anual
• Tomar o valor máximo de chuva diária de cada ano
de um período de N anos.
• Organizar N valores de chuva máxima em ordem
decrescente.
• A cada um dos valores pode ser associada uma
probabilidade de que este valor seja atingido ou
excedido em um ano qualquer.
• Fórmula empírica:
P  i (N  1)
Probabilidade x tempo de retorno
• Uma chuva que é igualada ou superada 10 vezes
em 100 anos tem um período de retorno de 10
anos. A probabilidade de acontecer esta chuva
em um ano qualquer é de 1/10 (ou 10 %).
• TR = 1/Prob
Tempos de retorno adotados
Dispositivo
considerado
Microdrenagem urbana
Drenagem urbana
Tempo de retorno
(anos)
2 a 5 anos
5 a 25 anos
Pontes e bueiros com
pouco trânsito
10 a 100 anos
Pontes e bueiros com
muito trânsito
100 a 1.000 anos
Grandes obras
hidráulicas
10.000 anos
Exemplo de uso da curva IDF
• Qual é a precipitação máxima de 1 hora de duração
em Porto Alegre?
• Qual é a precipitação máxima de 1 hora de duração
em Porto Alegre com 1% de probabilidade de ser
excedida em um ano qualquer?
• ps: IDF = intensidade, duração e freqüência.
Mapas de
chuva
Linhas de mesma
precipitação são
chamadas
ISOIETAS
Isoietas
• Apresentação em mapas
• Utiliza dados de postos pluviométricos
• Interpolação
Precipitação média numa bacia
• Precipitação = variável com grande heterogeneidade
espacial
Precipitação média numa bacia
• Média aritmética (método mais simples)
• 66+50+44+40= 200 mm
• 200/4 = 50 mm
66 mm
44 mm
• Pmédia = 50 mm
50 mm
40 mm
42 mm
Precipitação média numa bacia
• Problemas da média
• 50+70= 120 mm
• 120/2 = 60 mm
• Pmédia = 60 mm
Obs.: Forte precipitação
junto ao divisor não
está sendo considerada
120 mm
50 mm
70 mm
Precipitação média na bacia
Posto 2
1400 mm
Posto 1
1600 mm
Posto 3
900 mm
Precipitação média na bacia
1700
1600
Posto 2
1400 mm
1500
1300
Posto 1
1600 mm
1200
1000
Posto 3
900 mm
1700
1400
1200
1100
900
SIG
Precipitação média
por Thiessen
• Polígonos de Thiessen
Áreas de influência de
cada um dos postos
n
P   a i  Pi
i 1
120 mm
50 mm
ai = fração da área da bacia
sob influencia do posto I
Pi = precipitação do posto i
70 mm
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
1 – Linha que une dois
postos pluviométricos
próximos
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
2 – Linha que divide ao
meio a linha anterior
Definição dos
Polígonos de Thiessen
50 mm
2 – Linha que divide ao
meio a linha anterior
120 mm
Região de
dos postos
70 mm
75 mm
82 mm
influência
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
3 – Linhas que unem
todos
os
postos
pluviométricos vizinhos
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
4 – Linhas que dividem
ao meios todas as
anteriores
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
5 – Influência de
cada um dos postos
pluviométricos
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
5 – Influência de
cada um dos postos
pluviométricos
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
5 – Influência de
cada um dos postos
pluviométricos
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
5 – Influência de
cada um dos postos
pluviométricos
Definição dos
Polígonos de Thiessen
50 mm
120 mm
70 mm
75 mm
82 mm
5 – Influência de
cada um dos postos
pluviométricos
Definição dos
Polígonos de Thiessen
P  0,15.120 0,4.70  0,3.50  0,05.75  0,1.82
50 mm
30%
120 mm
70 mm
15%
40%
5%
10%
75 mm
82 mm
5 – Influência de
cada um dos postos
pluviométricos
Precipitação média
50 mm
• Média aritmética = 60 mm
120 mm
70 mm
• Média aritmética com
postos de fora da bacia =
79,4 mm
• Média por polígonos de
Thiessen = 73 mm
75 mm
82 mm
Falhas nos dados observados
• Preenchimento de falhas
(intervalo mensal; intervalo
anual)
Y
X1
X2
X3
120
74
85
122
83
70
67
93
55
34
60
50
-
80
97
130
89
67
94
125
100
78
111
105
Correlação entre chuvas anuais
Correlação entre chuvas anuais
Correção de falhas
• Se a correlação entre as chuvas de dois postos
próximos é alta, eventuais falhas podem ser
corrigidas por uma correlação simples.
• O ideal é utilizar mais postos para isto.
– Método da ponderação regional
Correção de falhas
• Posto Y apresenta falha
• Postos X1, X2 e X3 tem
dados.
• Ym é a precipitação média
do posto Y
PY 
1  PX1 PX2 PX3 



 Ym

3  Xm1 Xm 2 Xm 3 
• Xm1 a Xm3 são as médias
dos postos X
• PX1 a PX3 são as precipitações nos postos X1 a X3 no intervalo
de tempo em que Y apresenta falha.
• PY é a precipitação estimada em Y no intervalo que apresenta
falha.
Análise de consistência de dados
• Erros grosseiros
• Erros de transcrição
• "Férias" do observador
• Crescimento de árvores em torno do pluviômetro
• Mudança de posição
• O método Dupla Massa
Método Dupla Massa
Método Dupla Massa
Exercício
Precipitação
A = 78 mm
B = 84 mm
C = 64 mm
Exercício
Ano
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
Posto A
1658
1158
1161
1301
926
1784
1854
1233
1494
1411
1709
1258
1348
1350
Posto B
1672
1104
1264
1484
1000
1720
1850
1250
1396
1600
1649
1862
1329
1358
1602
1278
Posto C
1685
1226
1213
1392
1330
1771
1852
1751
1382
1850
1887
2014
1399
1369
1681
1153
Exercício
• Um balde com formato cônico foi deixado na chuva durante um
evento de 80 minutos de duração. Ao final do evento o balde, que
estava inicialmente vazio, apresentava o nível d’água h = 6 cm.
Qual foi a intensidade da chuva durante este evento (em
mm/hora)? A altura do balde é de 40 cm. O diâmetro maior do
balde é de 40 cm e o diâmetro menor de 25 cm.
Volume de tronco de cone
Exercício
Considerando a curva IDF do
DMAE para o posto pluviográfico
do Parque da Redenção, qual é a
intensidade da chuva com
duração de 60 minutos que tem
1% de probabilidade de ser
igualada ou superada em um
ano qualquer em Porto Alegre?
E qual a intensidade com Td = 20
minutos e probabilidade de
10%?
•
Exercício
• Uma análise de 40 anos de
dados revelou que a chuva média
anual em um local na bacia do rio
Uruguai é de 1800 mm e o desvio
padrão
é
de
350
mm.
Considerando que a chuva anual
neste local tem uma distribuição
normal, qual é o valor de chuva
anual de um ano muito seco, com
tempo de recorrência de 40
anos?