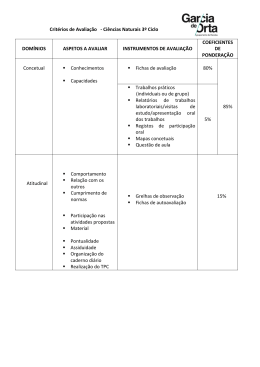
Álgebra Linear • TagusPark • Primavera ’11
Responsável: João Pedro Boavida
9 de Fevereiro de 2011
Este curso está organizado de forma algo diferente do habitual. Este documento explica as
opções que tomei e porque penso que vos ajudarão a aprender Álgebra Linear. Três aspectos
são especialmente importantes:
Usaremos várias formas de comunicação, não só para vos encorajar a esclarecer as vossas
dúvidas e a participar activamente na aula, mas também para minimizar os efeitos negativos
da frustração—a qual, apesar de ser frequentemente sintoma de progresso, tende a causar
relutância em fazer perguntas, sentimentos de isolamento, e desânimo.
As aulas servirão de apoio ao vosso estudo (e não ao contrário). A aprendizagem é sempre
um processo individual e o vosso sucesso dependerá crucialmente do trabalho regular; o meu
papel é orientar-vos e ajudar-vos a estudar eficazmente.
O papel principal da avaliação é ajudar-vos a aprender. Além dos testes, teremos avaliação
contínua frequente, para vos dar feedback regular sobre o vosso progresso. A nota final é
calculada de forma diferente da habitual.
Funcionamento
Como este é um curso de seis créditos, devem contar com cerca de uma hora de trabalho
por dia (para estudo, resolução de exercícios, esclarecimento de dúvidas, resolução de fichas
electrónicas), para além das aulas. É provável que tenham dúvidas e se sintam frustrados—
isso é normal e faz parte do processo. Por isso, é importante que todos se sintam confortáveis
a fazer perguntas (ou comentários construtivos) e que tenham uma ideia das dúvidas dos
vossos colegas.
RECEBERÃO GUIAS com o plano aproximado das aulas, sugestões de leitura, e exercícios
recomendados, para vos ajudar a identificar as ideias mais importantes (já que é fácil ficar-se
perdido no mar de informação), perceber as relações entre os diferentes tópicos, e decidir
como organizar o vosso estudo.
O LIVRO DE APOIO é o mesmo do semestre passado: David C. Lay, Linear Algebra and Its
Applications, third edition (update), Pearson Education. Embora respeitando as convenções e
notações do livro, não vamos sempre seguir a mesma sequência (os guias irão indicando as
secções relevantes).
A AVALIAÇÃO CONTÍNUA incentiva o estudo regular (alinhando os benefícios de curto prazo
com os objectivos a longo prazo) através de fichas electrónicas (cerca de duas por semana)
baseadas nos exercícios recomendados ou em assuntos discutidos nas leituras ou nas aulas.
Embora opcional, a avaliação contínua pode ter um peso substancial na nota final (incluindo
na época especial de Julho de 2011) e reduzir (parcial ou totalmente) a nota mínima necessária
nos testes.
•
1/4
Álgebra Linear • TagusPark • Primavera ’11
João Pedro Boavida
9 de Fevereiro de 2011
TEREMOS INQUÉRITOS (anónimos) no Fénix, sobre o vosso acompanhamento do material,
dúvidas que tenham, ou comentários sobre o funcionamento das aulas. Os resultados serão
disponibilizados a toda a turma através do Fénix, para que todos possam saber quais são as
dúvidas e dificuldades mais frequentes.
USAREMOS OS FÓRUNS (não anónimos) do Fénix para discutir dúvidas (mas não as fichas
electrónicas), o funcionamento das aulas, ou questões levantadas nos inquéritos.
O HORÁRIO DE DÚVIDAS será logo após as aulas teóricas, até às 19:15. Vão ter directamente à
sala 2N2.2 ou ao meu gabinete. (Excepto em dias de teste, podem procurar-me a outras horas
nos mesmos dias. Em particular, devem conseguir encontrar-me entre as 9:00 e a primeira
aula prática.)
A MELHOR FORMA DE ME CONTACTAR (fora das aulas e dos horários de dúvidas) é enviando email
para <[email protected]>. Ocasionalmente poderei demorar dois ou três dias a
responder, e nas 48 horas anteriores a cada teste planeio não responder a dúvidas por email.
AS AULAS serão fortemente influenciadas pelas discussões no fórum, as dúvidas levantadas
nos inquéritos, e as dificuldades que tenham nas fichas electrónicas. É crucial que estudem
regularmente, para que nas aulas possamos concentrar-nos no material mais complicado, em
vez de gastar tempo com o material mais fácil que todos podem perceber sozinhos. Alguns
assuntos serão discutidos só nas aulas teóricas ou só nas aulas práticas, e portanto o ideal
é frequentarem tanto umas como as outras. (Porém, eu sei que alguns de vocês têm aulas
sobrepostas com a nossa aula teórica. Nesse caso, talvez valha a pena combinarem trocar
apontamentos das aulas com colegas vossos.)
FAÇAM PERGUNTAS, seja durante as aulas, nos horários de dúvidas, por email, no fórum do
Fénix, ou nos inquéritos. Identifiquem e esclareçam as vossas dúvidas em tempo útil.
RESPEITEM os vossos colegas, bem como o seu tempo e trabalho. É importante que a aula
seja produtiva, e que todos sintam que podem participar activamente. Em particular, não
conversem durante a aula sobre assuntos externos à aula, não causem distracções, e respeitem
as intervenções dos vossos colegas.
Método de Avaliação
A AVALIAÇÃO CONTÍNUA será feita através de fichas electrónicas (cerca de duas por semana, com
um prazo de cerca de uma semana para cada uma). Ao longo de todo o semestre, haverá um
total de 63 perguntas. A nota C da avaliação contínua é o número de respostas correctas,
dividido por 3. Assim, C é um múltiplo de 1/3, com 0 ≤ C ≤ 21. As fichas devem ser resolvidas
individualmente, mas é permitido consultar apontamentos pessoais.
•
2/4
Álgebra Linear • TagusPark • Primavera ’11
João Pedro Boavida
9 de Fevereiro de 2011
OS TRÊS TESTES têm notas inteiras, com 0 ≤ T1 , T2 ≤ 25 e 0 ≤ T3 ≤ 50. Os testes T1 e T2
terão a duração de 0:50, o teste T3 terá a duração de 1:30. Haverá um exame de recurso, em
que poderão tentar melhorar ou só a primeira metade M1 = T1 + T2 (duração de 1:30), ou só
a segunda metade M2 = T3 (duração de 1:30), ou o total E = M1 + M2 (duração de 3:00). A
nota correspondente é alterada apenas se tiver melhorado.
A pontuação combinada nos testes ou exame é E = M1 + M2 = T1 + T2 + T3 . Excepto se
E for obtida totalmente no exame de recurso, aplica-se a nota mínima M1 , M2 ≥ 21 − C .
Os testes/exame são feitos individualmente. Não é permitido usar equipamento electrónico,
nem consultar colegas, apontamentos, ou quaisquer materiais.
A NOTA FINAL é NF =
o
çã
ia
l
a
7
av
0
0
1
co
ua
ín
t
n 14
2
C
3
21
4
0
E·
99−C
99
5
+C
(a figura ilustra o efeito desta fórmula).
pontuação combinada nos testes ou exame E = M1 + M2 = T1 + T2 + T3
10
20
30
40
50
60
70
80
90
100
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
nota final NF , arredondada ao inteiro mais próximo
A nota final NF é identificada pelas faixas verticais. A avaliação contínua C é opcional e tem um
peso tanto maior quanto mais possa ajudar a passar. A nota mínima para ser avaliado por testes é
M1 , M2 ≥ 21 − C . Os círculos assinalam alguns exemplos concretos:
• Com C = 0, é preciso M1 , M2 ≥ 21 (42% em cada metade) para ser avaliado por testes, E ≥ 48
para obter NF > 9.5, E ≥ 68 para obter NF > 13.5, e E ≥ 88 para obter NF > 17.5.
• Com C = 7, é preciso M1 , M2 ≥ 14 (28% em cada metade) para ser avaliado por testes, E ≥ 44
para obter NF > 9.5, E ≥ 66 para obter NF > 13.5, e E ≥ 87 para obter NF > 17.5.
• Com C = 14, é preciso M1 , M2 ≥ 7 (14% em cada metade) para ser avaliado por testes, E ≥ 40
para obter NF > 9.5, E ≥ 63 para obter NF > 13.5, e E ≥ 86 para obter NF > 17.5.
• Com C = 21, é preciso E ≥ 34 para obter NF > 9.5, E ≥ 60 para obter NF > 13.5, e
E ≥ 85 para obter NF > 17.5.
NA ÉPOCA ESPECIAL DE 2011, a nota C , se obtida neste semestre, será contabilizada da mesma
forma (com a nota do exame convertida para o intervalo 0 ≤ E ≤ 100).
TRABALHADORES-ESTUDANTES ou outros alunos com razões válidas e documentadas que
realmente os impeçam de fazer os testes/exame nas datas marcadas, devem contactar-me logo
que saibam desse conflito. Baseado nas circunstâncias de cada caso, decidirei se o exame de
recuperação permite resolver o conflito, ou se é necessário planear outras alternativas.
•
3/4
Álgebra Linear • TagusPark • Primavera ’11
João Pedro Boavida
9 de Fevereiro de 2011
Calendário Aproximado
21 DE FEVEREIRO–4 DE MARÇO. Introdução. “Mapa” de toda a álgebra linear. Revisão de
operações de matrizes, combinações lineares, operações elementares e método de Gauss.
9–23 DE MARÇO. Espaços vectoriais, espaços de combinações lineares e espaços de soluções.
Núcleo, espaço das linhas, espaço das colunas. Classificação de sistemas.
24 DE MARÇO. Teste 1, na aula teórica.
28 DE MARÇO–29 DE ABRIL. Transformações lineares, representação matricial, mudança de base.
Valores, vectores, e subespaços próprios. Determinantes e volumes. Diagonalização.
3 DE MAIO. Teste 2, na aula teórica.
4–17 DE MAIO. Produtos internos, bases ortonormadas. Diagonalização de matrizes simétricas
e ortogonais. Transformações em 2-D e 3-D. Equações de k-planos.
28 DE MAIO. Teste 3, no sábado após o fim das aulas.
16 DE JUNHO. Exame de recuperação.
ÉPOCA ESPECIAL em Julho, em data a anunciar.
•
4/4