CPV seu Pé Direito no INSPER
INSPER Resolvida – 2/novembro/2014 – Prova A
ANÁLISE QUANTITATIVA E LÓGICA
Resolução:
Utilize as informações a seguir para as questões 01 e 02.
Os ingressos para a pré-estreia mundial de um filme começaram
a ser vendidos 20 dias antes da exibição do filme, sendo que:
● nos 10 primeiros dias desse período, as vendas foram feitas
exclusivamente nas bilheterias;
● nos dez últimos dias, as vendas ocorreram simultaneamente
nas bilheterias e pela internet.
Para t = 0 dia Þ v = 0
Para t = 10 dias Þ v = 20 milhões
Portanto V(t) = 2t
Considere que t representa o tempo, em dias, desde o início
das vendas e v(t) o total de ingressos vendidos, em milhões,
até o tempo t.
01. Durante as vendas exclusivas nas bilheterias, a capacidade
de atendimento dos guichês dos cinemas do mundo todo, ao
longo do tempo, era sempre a mesma, totalizando a venda
de 2 milhões de ingressos por dia. Assim, o gráfico que
melhor descreve v(t) para esse período, em função de t, é:
Alternativa C
02. No período de vendas simultâneas nas bilheterias e pela
internet, a função v(t) é dada por:
v(t) = − 0,1t2 + 4t − 10.
O número de ingressos vendidos apenas nos 10 dias que
antecederam a exibição do filme foi:
a)
b)
c)
d)
e)
10 milhões
20 milhões
30 milhões
40 milhões
50 milhões
Resolução:
CPV
INSPERNOV2014
Se v(t) = –0,1 t2 + 4t – 10 é válido somente nos dias de vendas
simultâneas, então o número de ingressos é dado por:
v(20) – v(10) = [–0,1 (20)2 + 4 (20) – 10] – [–0,1 (10)2 + 4 (10) – 10]
v(20) – v(10) = 10 milhões
Alternativa A
1
2
INSPER – 02/11/2014
Seu Pé D ireito
nas
Utilize as informações a seguir para as questões 03 a 05.
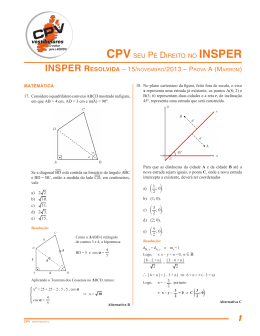
A figura abaixo mostra o alvo de uma academia de arco e flecha.
A pontuação que um jogador recebe ao acertar uma flecha em
cada uma das faixas circulares está indicada na respectiva faixa.
O raio do círculo maior mede 60 cm, o do menor mede 10 cm e a
diferença entre os raios de quaisquer dois círculos consecutivos
é de 10 cm. Todos os círculos têm o mesmo centro.
Melhores Faculdades
04. Para treinar, Rafael posicionou o seu arco a 5 metros do alvo
e lançou uma flecha utilizando uma mira a laser, mostrando
que sua flecha foi lançada numa direção perpendicular ao
plano do alvo, na direção do centro dos círculos. Entretanto,
o vento e o efeito da gravidade deslocaram sua flecha, que
atingiu o alvo 12 cm para a esquerda e 9 cm para baixo
em relação ao centro dos círculos. Rafael afastou o arco
para 15 metros de distância do alvo, mantendo a mesma
direção da mira e lançou mais uma flecha. Se o desvio
provocado pelo vento e pelo efeito da gravidade nesse
novo lançamento se manteve proporcional à distância de
lançamento, a pontuação correspondente à faixa em que
essa segunda flecha atingiu o alvo foi:
a) 10 pontos
b) 20 pontos
c) 40 pontos
d) 80 pontos
e) 160 pontos
Resolução:
Pelo texto, a flecha atinge o alvo no ponto A:
12 cm
9 cm
03. A soma das áreas das faixas em cinza na figura é igual a:
a)
b)
c)
d)
e)
900π cm2
1100π cm2
1300π cm2
1500π cm2
1700π cm2
Resolução:
Se S1 , S2 , S3 , S4 e S5 são, respectivamente, as áreas dos círculos
de raio 10, 20, 30, 40 e 50 cm, então a soma das áreas das faixas
em cinza é dada por:
S = π (502 – 402 + 302 – 202 + 102)
S = 1500 π cm2
CPV
INSPERNOV2014
A
Aplicando o Teorema de Pitágoras, temos que x = 15 cm,
portanto na faixa dos 160 pontos.
Ao afastar para uma distância de 15 metros, mantida a
proporcionalidade, o alvo será atingido a uma distância de
3x = 45 cm, portanto na faixa de 20 pontos.
Alternativa B
05. O treinador de Rafael propôs a ele o cálculo de um índice
de precisão que avalie a sua habilidade como atirador. Para
calculá-lo, Rafael precisa:
Alternativa D
x
S = S5 – S 4 + S 3 – S 2 + S 1
0
● multiplicar cada pontuação possível do alvo pela
probabilidade de ele acertar uma flecha na faixa
correspondente;
● somar os resultados das multiplicações feitas para as
6 faixas.
Rafael registrou na tabela a seguir as pontuações que ele
obteve durante um treino no qual ele lançou 200 flechas.
Pontuação 10 20 40 80 160 320
Acertos
20 30 40 50 40 20
Seu Pé D ireito
nas
Melhores Faculdades
Usando os dados da tabela para estimar as probabilidades,
o índice de precisão de Rafael é:
a) 96
b) 97
c) 98
d) 99
e) 100
Resolução:
Pelo texto, o índice de precisão é:
I=
I = 1 + 3 + 8 + 20 + 32 + 32
I = 96
20
30
40
50
40
20
.10 +
.20 +
.40 +
.80 +
.160 +
.320
200
200
200
200
200
200
Alternativa A
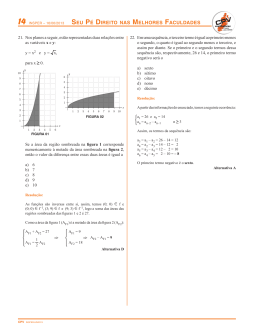
06. O número n de pessoas presentes em uma festa varia ao
longo do tempo t de duração da festa, em horas, conforme
mostra o gráfico a seguir.
INSPER – 02/11/2014
3
07. Uma operadora de telefonia celular oferece a seus clientes
dois planos:
Superminutos: o cliente paga uma tarifa fixa de R$ 100,00
por mês para os primeiros 200 minutos que utilizar. Caso
tenha consumido mais minutos, irá pagar R$ 0,60 para
cada minuto que usou a mais do que 200.
Supertarifa: o cliente paga R$ 60,00 de assinatura mensal
mais R$ 0,40 por minuto utilizado.
Todos os meses, o sistema da operadora ajusta a conta de
cada um de seus clientes para o plano mais barato, de acordo
com as quantidades de minutos utilizadas. Nesse modelo,
o plano Superminutos certamente será selecionado para
consumidores que usarem
a)
b)
c)
d)
e)
menos do que 60 minutos no mês.
entre 40 e 220 minutos no mês.
entre 60 e 300 minutos no mês
entre 100 e 400 minutos no mês.
mais do que 400 minutos no mês.
Resolução:
C1: Plano Superminutos
C1 (t) = 100 + (t – 200) . 0,60
C2: Plano Supertarifa
C2 (t) = 60 + 0,40 . t
Assim: C1 (t) < C2 (t) e C2 (t) > 100
100 + 0,6 t – 120 < 60 + 0,4 t
0,2 t < 80
t < 400 e 60 + 0,40 t > 100
e
0,40 t > 40
e t > 100
O Plano Superminutos será selecionado para consumidores que
usarem 100 < t < 400 minutos por mês
Alternativa D
Das opções abaixo, aquela que melhor descreve a função
n(t) é:
a)
b)
c)
d)
e)
n(t) = −10t2 + 4t + 50
n(t) = −10t2 + 40t + 50
n(t) = −10t2 + 4t
n(t) = −t2 + 40t
n(t) = −10t2 + 40t
Utilize as informações a seguir para as questões 08 e 09.
Uma artista plástica está criando uma nova obra, que será um
quadro com alto relevo de formas geométricas. Para iniciar o
projeto, ela desenhou o quadrado base da obra, mostrada abaixo.
Resolução:
O gráfico do enunciado é de uma função quadrática dada por:
n(t) = a . (t) . (t – 4) e
n (2) = 40 Þ – 4a = 40 Þ a = – 10
Assim, n(t) = – 10 t2 + 40t
Alternativa E
Esse quadrado tem 40 cm de lado e o ponto P foi posicionado
8 cm para a direita e 8 cm para baixo do ponto A. Tra¸cando a
diagonal do quadrado e tomando o ponto P como vértice, ela
construiu o triângulo em preto e, usando a simetria em relação
à diagonal, ela construiu o triângulo em branco, com vértice
no ponto Q.
INSPERNOV2014
CPV
4
INSPER – 02/11/2014
Seu Pé D ireito
nas
Em seguida, reproduzindo esse quadrado base 16 vezes, ela
construiu o quadro em relevo mostrado abaixo, elevando
2 tetraedros sobre cada quadrado base, cada um com altura de
6 cm em relação ao plano do quadrado base, conforme ilustra
a figura a seguir.
Melhores Faculdades
Na figura:
BC é a diagonal do quadrado cujo lado mede 40 cm e portanto
BC = 40
PH é a diagonal do quadrado cujo lado mede 12 cm e portanto
PH = 12
Então, a área do triangulo PBC é:
APBC =
2 cm;
2 cm.
40
2 . 12
2
2 = 480 cm2
Alternativa B
09. Para garantir o efeito visual que desejava, a artista plástica
fez as faces dos tetraedros de material transparente e
encheu com um líquido contendo material reflexivo. O
volume de líquido necessário para encher todo o quadro
é de, aproximadamente,
08. A área do triângulo PBC do quadrado base é igual a:
a)
b)
c)
d)
e)
320 cm2
480 cm2
640 cm2
800 cm2
960 cm2
8
45 litros
47 litros
49 litros
51 litros
53 litros
Resolução:
A base de cada tetraedro será equivalente ao triângulo ABC e
40 . 40
portanto a área da base é
= 800 cm2.
2
O volume dos 32 tetraedros pedidos é:
1
Vtotal = 32 .
. 800 . 6 = 51.200 cm3 = 51,2 litros
3
Alternativa D
Resolução:
A
a)
b)
c)
d)
e)
12
20
8
C
10. Considere dois números positivos x e y, com x > y, tais
que
x + y + x – y = 8
x2 – y2 P
12
H
Nessas condições, 2x é igual a
a)
b)
c)
d)
e)
= 15.
31
32
33
34
35
Resolução:
20
B
CPV
INSPERNOV2014
Se quadrarmos a 1a equação, temos:
(
x+y+2.
2x + 2 .
2x + 2 . (15) = 64
2x = 34
x+y+
x – y) = (8)2
2
x+y.
x – y + x – y = 64
x2 – y2 = 64
Alternativa D
Seu Pé D ireito
nas
Melhores Faculdades
11. No jogo da multiplicação unitária deve-se preencher cada
um dos círculos sombreados na figura com um dos números
1 ou −1. Em seguida, deve-se multiplicar os números dois
a dois, obtendo um resultado para cada linha que liga dois
círculos. Por último, deve-se somar os resultados de todas
essas multiplicações, obtendo o resultado do jogo.
O menor resultado que esse
jogo pode ter é:
a)
b)
c)
d)
e)
INSPER – 02/11/2014
5
12. O gráfico abaixo representa o número de gols marcados
(barras em cinza) e o número de gols sofridos (barras em
preto) por uma equipe de futebol de salão nos 10 jogos de
um campeonato.
0
−1
−2
−4
−6
Resolução:
Se tivermos todos iguais a 1:
1
1
1
Se tivermos três 1 e um –1:
1
1
Se tivermos dois 1 e dois –1:
1
c) 0
A média do saldo de gols é:
x=
2 + 2 + (–2) + 4 + 0 + (–2) + 0 + (–1) + (–3) + 3
= 0,3
10
Alternativa E
1–1+1–1–1–1=–2
–1
–1
–1
–1 + 1 + 1 – 1 – 1 + 1 = 0
–1
E, finalmente, se tivermos todos iguais a –1:
–1
–1
A soma a + b e a diferença b − a são, respectivamente,
iguais a:
a) 3 e 1
d) −1 e π
–1
Então, o menor resultado do jogo é –2
b) 1 e −3
e) 3 e −1
c) π e 1
Resolução:
+1 + 1 + 1 + 1 + 1 + 1 = 6
–1
b) –0,1
e) 0,3
Se tivermos três –1 e um 1:
1
a) –0,3
d) 0,1
13. A figura abaixo representa o gráfico da função
f (x) = a cos(x) + b.
1
–1
1–1–1+1–1+1=0
–1
Resolução:
1
Em cada partida, o saldo de gols da equipe é dado pela
diferença entre os gols marcados e os gols sofridos. A média
dos saldos de gols da equipe nesses dez jogos é igual a:
1+1+1+1+1+1=6
1
Alternativa C
x = π Þ f (π) = –1 Þ a cos π + b = –1 Þ b – a = –1
x = 2π Þ f (2π) = 3 Þ a cos 2π + b = 3 Þ a + b = 3
Alternativa E
INSPERNOV2014
CPV
6
Seu Pé D ireito
INSPER – 02/11/2014
nas
14. A fila para entrar em uma balada é encerrada às 21h e,
quem chega exatamente nesse horário, somente consegue
entrar às 22h, tendo que esperar uma hora na fila. No
entanto, quem chega mais cedo espera menos tempo: a
cada dois minutos de antecipação em relação às 21h que
uma pessoa consegue chegar, ela aguarda um minuto a
menos para conseguir entrar. Se uma pessoa não quiser
esperar nem um segundo na fila, o horário máximo que
ela deve chegar é:
a)
b)
c)
d)
e)
Melhores Faculdades
Utilize as informações a seguir para as questões 16 e 17.
O Sr. Antônio resolveu construir um poço em seu sítio. Ele
passou ao engenheiro o esquema abaixo, indicando a posição da
piscina e do vestiário em relação à localização da casa.
19h
19h15min
19h30min
19h45min
20h
Resolução:
Montando duas equações para os horários de chegada (C), de
1
entrada (E) e levando em consideração que 1 min =
hora temos:
60
2k
k
k
C = 21 –
E=C+ 1–
Þ E = 22 –
60
60
20
( )
Para uma pessoa entrar na balada no momento que chegar
devemos ter:
C = E
Portanto, C = E = 19 horas
Þ
21 –
2k
k
= 22 –
Þ
60
20
k = 60
Alternativa A
15. Uma rede de cafeterias vende copos térmicos para que o
cliente possa comprar seu café e levá-lo em seu próprio
recipiente. Como, nesse caso, a empresa economiza com os
copos descartáveis, quando o cliente usa o copo térmico da
rede, recebe um desconto de R$ 0,25 no café. Para decidir
se compraria um copo térmico, um cliente calculou que
seria necessário receber este desconto 397 vezes para que
ele recuperasse o valor a ser pago no copo.
O preço do copo térmico é um valor entre:
a)
b)
c)
d)
e)
16. O Sr. Antônio disse ao engenheiro que queria o poço numa
localização que estivesse à mesma distância da casa, da
piscina e do vestiário. Para atendê-lo o engenheiro deve
construir o poço na posição, em relação à casa, dada por,
aproximadamente,
a)
b)
c)
d)
e)
4,2 m para o leste e 13,8 m para o norte.
3,8 m para o oeste e 13,1 m para o norte.
3,8 m para o leste e 13,1 m para o norte.
3,4 m para o oeste e 12,5 m para o norte.
3,4 m para o leste e 12,5 m para o norte.
Resolução:
Tomando a casa como origem de um plano cartesiano, temos a
seguinte figura:
y
C (12; 24)
B (–8; 20)
PISCINA
VESTIÁRIO
R$ 85,00 e R$ 90,00.
R$ 90,00 e R$ 95,00.
R$ 95,00 e R$ 100,00.
R$ 105,00 e R$ 110,00.
R$ 110,00 e R$ 115,00.
P (x; y)
POÇO
A (0; 0)
CASA
x
Resolução:
Pelo enunciado, temos:
QUANTIDADE
.
DESCONTO
Preço do copo = 397 0,25
=
99,25
O preço do copo térmico é um valor entre R$ 95,00 e R$ 100,00
Alternativa C
CPV
INSPERNOV2014
Seja P (x; y) um ponto tal que PA = PB = PC.
Assim, temos:
PA
= (x – 0)2 + (y – 0)2 =
PB
(x + 8)2 + (y – 20)2
x2 + y2 = x2 + 16x + 64 + y2 – 40y + 400 Þ 2x – 5y + 58 = 0
Seu Pé D ireito
PA
= (x – 0)2 + (y – 0)2 =
nas
Melhores Faculdades
PC
(x – 12)2 + (y – 24)2
x2 + y2 = x2 – 24x + 144 + y2 – 48y + 576 Þ x + 2y – 30 = 0
Resolvendo o sistema, temos:
2x – 5y + 58 = 0
x @ 3,8
x + 2y – 30 = 0
y @ 13,1
INSPER – 02/11/2014
7
18. A relação entre o investimento x (em milhões de reais) na
propaganda para a divulgação de um produto e o número
k de potenciais consumidores (em milhões) atingidos por
essa campanha é dada por uma função k(x), cujo gráfico
está representado a seguir.
Alternativa C
17. Aproveitando que iria iniciar uma obra, o Sr. Antônio decidiu
construir uma quadra. Sua esposa, no entanto, exigiu as
seguintes condições para que se definisse a localização da
quadra, para que ninguém viesse suado para a casa:
● as localizações da quadra, do vestiário e da casa devem
estar sobre uma mesma linha reta;
● o vestiário deve ser um ponto do segmento de reta que
liga a casa à quadra.
O Sr. Antônio fez uma anotação adicional em seu esquema
para o arquiteto. Das opções a seguir, a única que atende às
exigências impostas pela esposa do Sr. Antônio é:
a)
b)
c)
Para avaliar o retorno dessa campanha, calculam-se dois
índices, como se segue:
● identificam-se os valores x1, x2 e x3 para os quais 1, 2
e 4 milhões de potenciais consumidores são atingidos,
respectivamente;
x2
● a razão
resulta no índice Ia;
x1
x3
resulta no índice Ib.
x2
● a razão
Para a função k(x) acima, o valor de
a)2
b) 3
c) 4
d)5
e) 6
Ib + Ia
é:
Ib – Ia
Resolução:
d)
No gráfico obtemos:
1 = f (x1) Þ x1 = 1/3
2 = f (x2) Þ x2 = 1
4 = f (x3) Þ x3 = 5
e)
Ia =
Resolução:
Pelas restrições da esposa do Sr. Antônio, temos que a quadra ficará
mais afastada do que o vestiário (tanto ao norte quanto a oeste).
A única alternativa que satisfaz as condições da esposa é a
alternativa a.
Alternativa A
Ib =
x2
x1
x3
x2
Ib + Ia
Ib – Ia
=
1
=3
1/3
=
5
=5
1
=
5+3
=4
5–3
Alternativa C
INSPERNOV2014
CPV
8
INSPER – 02/11/2014
Seu Pé D ireito
nas
19. O esquema abaixo mostra as duas rodas dentadas e a correia
do sistema de transmissão de uma bicicleta.
Considere que a correia se ajuste sem folga aos dentes de
ambas as rodas. Se R é a medida do raio da circunferência que
dá forma à roda maior e r é a medida do raio da circunferência
R
que dá forma à roda menor, então a razão é igual a:
r
Melhores Faculdades
21. A diferença entre a maior e a menor raiz de p(x) é igual a:
a) 5
b) 6
c) 7
d) 8
Resolução:
Pelo gráfico, f (2) = 0, então f (2) = α p (2) Þ 0 = α p (2) Þ p (2) = 0
Assim, 2 é raiz de p (x) e:
a) 2,0
2
1
–1
–22
40
b) 2,5
1
1
–20
0
c) 3,0
d) 3,5
e) 4,0
Resolução:
Observando a figura dada temos como referência de medida de
comprimento o número de dentes de cada roda.
C2: roda menor → 8 dentes
20 = 2 . π . R e 8 = 2 . π . r
R
2.π.R
20
=
Þ
= 2,5
r
8
2.π.r
p(x) =
−
(x – 2) (x2 + x – 20) = 0
Portanto:
x2 + x – 20 = 0
x = –5 ou x = 4
4 – (–5) = 9
do quadrado, então
Alternativa B
Considere o polinômio dado por
x2
p (x) = (x – 2) (x2 + x – 20)
Alternativa E
Se a é a medida do segmento AB e l é a medida do lado
Utilize as informações a seguir para as questões 20 e 21.
x3
22. Na figura, AD é um diâmetro da circunferência que contém
o lado BC do quadrado sombreado, cujos vértices E e F
pertencem à circunferência.
C1: roda maior → 20 dentes
e) 9
− 22x + 40.
A figura a seguir mostra
parte do gráfico da função f,
dada por f (x) = α . p(x),
em que α é um número real.
l é igual a:
a
a)5 – 2
b)
5–1
2
5+1
2
c)
5
d)
2
e)5 + 2
Resolução:
20. O valor de α é:
a) 0,05 b) 0,5
d)
5e)
20
c) 2
l2 = a (l + a), então
Pela figura abaixo, devemos ter:
l2 – al – a2 = 0 Þ Δ = a2 + 4a2 = 5a2 e
l=
Portanto:
a±a
2
a (1 ± 5)
2
1+ 5
l
=
2
a
5
=
Resolução:
Observando o gráfico temos que
f (0) = 2 Þ 2 = α . p (0)
2 = α . (40) Þ α = 0,05
l
a
Alternativa A
l+a
l
Alternativa C
CPV
INSPERNOV2014
Seu Pé D ireito
nas
Melhores Faculdades
23. Em uma noite, a razão entre o número de pessoas que estavam
jantando em um restaurante e o número de garçons que as
atendiam era de 30 para 1. Em seguida, chegaram mais 50
clientes, mais 5 garçons iniciaram o atendimento e a razão
entre o número de clientes e o número de garçons ficou em
25 para 1. O número inicial de clientes no restaurante era:
a) 250 b) 300
d)
400e)
450
c) 350
Resolução:
Sejam C o número de clientes e G o número de garçons.
Então:
C
30
=
C = 30 G
G
1
Þ
Þ
C = 450
G = 15
C + 50
25
=
G+5
1
30 G + 50 = 25 G + 125
Alternativa E
24. Uma empresa tem 15 funcionários e a média dos salários
deles é igual a R$ 4.000,00. A empresa é dividida em três
departamentos, sendo que:
A média dos salários dos outros funcionários, do departamento
comercial, é igual a:
a)
b)
c)
d)
e)
R$ 3.800,00
R$ 3.900,00
R$ 4.000,00
R$ 4.100,00
R$ 4.200,00
Sejam:
å adm = a soma dos salários dos 6 funcionários administrativos
å des = a soma dos salários dos 4 funcionários de desenvolvimento
å com = a soma dos salários dos 5 outros funcionários
Então:
å adm = 3750 . 6 = 22500
22500 + 16500 + å com
e 4000 =
15
å des = 4125 . 4 = 16500
a)
b)
c)
d)
e)
19 e 37
20 e 37
20 e 38
19 e 38
20 e 39
Resolução:
Ao dividirmos 633 por 33 obtemos quociente 19 e resto 6, portanto
o número mínimo de pessoas deve ser 19 + 1 = 20.
Ao dividirmos 633 por 17 obtemos quociente igual a 37 e resto 1,
portanto o número máximo de pessoas é 37.
Alternativa B
26. Para percorrer 1 km, o jovem Zeno adota a estratégia de
dividir seu movimento em várias etapas, percorrendo, em
cada etapa, metade da distância que ainda falta até o ponto
de chegada. A tabela mostra a distância percorrida por ele
em cada etapa.
Resolução:
de onde obtemos
21000
= R$ 4.200,00
5
Alternativa E
Etapa
Distância percorrida (km)
1
1/2
2
1/4
3
1/8
n
1/2n
Ao final da etapa n, a distância total percorrida por Zeno
será igual a:
2n – 1
2n + 1
a) n b) n 2
2
2n – 1
2n + 1
d) n e) n
2
2
c)
n
2n
Resolução:
A distância total percorrida por Zeno é a soma de uma P.G. finita
1
1
de primeiro termo , razão
e n termos.
2
2
Assim,
å com = 21000.
Logo, a média dos salários dos 5 outros funcionários é igual a:
9
25. Um bazar beneficente arrecadou R$ 633,00. Nenhum dos
presentes contribuiu com menos de R$ 17,00, mas também
ninguém contribuiu com mais de R$ 33,00. O número
mínimo e o número máximo de pessoas presentes são,
respectivamente, iguais a:
● A média dos salários dos 6 funcionários administrativos
é igual a R$ 3.750,00.
● A média dos salários dos 4 funcionários de
desenvolvimento de produto é igual a R$ 4.125,00.
INSPER – 02/11/2014
D =
D=
1
.
2
(( ) )
2n – 1
2n
1 n
–1
2
1
–1
2
=
( )
1 1 – 2n
.
2
2n
1
–
2
= –
( )
1 – 2n
2n
Alternativa A
INSPERNOV2014
CPV
10
INSPER – 02/11/2014
Seu Pé D ireito
nas
Resolução:
27. Na figura, que mostra o gráfico
da função polinomial
3x3
−
16x2
p(x) =
os valores a e c são tais que
a + c = 4.
Dessa forma,
o valor de c é igual a:
a) 1 +
7
b) 2 +
3
c) 2 +
6
d) 3 +
2
e) 3 +
5
9
.
algarismos
de 1 a 9
.
C5,2
.
↓
escolha de
2 algarismos
de paridades
diferentes dos
dois primeiros
P3
↓
permutação
dos 3
escolhidos
Portanto, 9 . 4 . 10 . 6 = 2160 números
Alternativa D
29. A proposição “se você trabalhar muito, então você
enriquecerá” é equivalente à proposição:
3x3 – 16x2 + 19x = 4
Þ 3x3 – 16x2 + 19x – 4 = 0 Þ a + b + c =
Pelo enunciado a + c = 4, assim b =
Fazendo Briot-Ruffini, temos:
– 16
.
C4,1
↓
escolha de
1 algarismo
de mesma
paridade do
primeiro
3
.
↓
Como a, b e c são as raízes da equação p (x) = 4, temos:
4
3
O número total de anos de sorte é dado por:
+ 19x,
Resolução:
Melhores Faculdades
19
“se você não trabalhar muito, então não enriquecerá”.
“se você enriquecer, então você trabalhará muito”.
“não trabalhe muito, ou você enriquecerá”.
“se você enriquecer, então você não trabalhará muito”.
“se você trabalhar muito, então não enriquecerá”.
Resolução:
16
3
4
.
3
–4
3 – 12
3
0
3x2 – 12x + 3 = 0 de onde obtemos a = 2 –
a)
b)
c)
d)
e)
3ec=2+
3
Consideremos as proposições
p: você trabalha muito,
~p: você não trabalha muito
q: você enriquecerá
p → q: se você trabalhar muito, então você enriquecerá.
As proposições “p → q” e “~p ou q” são equivalentes.
Temos:
Alternativa B
~p
q
p→q
~p ou q
V
F
V
V
V
V
F
F
F
F
F
V
V
V
V
F
V
F
V
V
p
28. Certa comunidade mística considera 2015 um ano de sorte.
Para tal comunidade, um ano é considerado de sorte se, e
somente se, é formado por 4 algarismos distintos, sendo 2
pares e 2 ímpares. No período que vai do ano 1000 até o
ano 9999, o número total de anos de sorte é igual a:
30. O rótulo de uma embalagem de suco concentrado sugere
que o mesmo seja preparado na proporção de sete partes de
água para uma parte de suco, em volume. Carlos decidiu
preparar um copo desse suco, mas dispõe apenas de copos
cônicos, mais precisamente na forma de cones circulares
retos.
CPV
a) 1680
b) 1840
c) 1920
d) 2160
e)2400
INSPERNOV2014
Assim, “~p ou q” pode ser descrito pela expressão “não trabalhe
muito, ou você enriquecerá”.
Alternativa C
Para seguir exatamente as instruções do rótulo, ele deve
acrescentar no copo, inicialmente vazio, uma quantidade
de suco até:
a) metade da altura.
c) um oitavo da altura.
e) sete oitavos da altura.
b) um sétimo de altura.
d) seis sétimos da altura.
Seu Pé D ireito
nas
Melhores Faculdades
A
H
31. Para que o carro perca 80% do seu valor, é necessário que
se passem
h
A
7
=
Þ A = 7S
S
1
Pelo enunciado temos:
Como a quantidade de suco é semelhante à quantidade total,
( ) (
11
Informação II
Um carro, que no ato da compra vale R$ 40.000,00, tem uma
desvalorização de 15% ao ano. Ou seja, após um ano, o carro
tem, a cada instante, um valor 15% menor do que o valor que
tinha exatamente um ano antes.
Resolução:
S
INSPER – 02/11/2014
) ( )
h 3
S
h 3 S
=
Þ
=
H
A+S
H
8S
h
1
H
Þ
=
Þ h=
H
2
2
a)
b)
c)
d)
e)
entre 5 e 6 anos.
entre 6 e 7 anos.
entre 7 e 8 anos.
entre 8 e 9 anos.
entre 9 e 10 anos.
Resolução:
Portanto, deve-se acrescentar suco até a metade da altura.
Alternativa A
Utilize as informações a seguir para as questões 31 e 32.
Informação I
A figura a seguir exibe parte do gráfico da função
f (x) = log0,85 x, cujo domínio é {x Î  | 0 < x ≤ 0, 85}.
O carro sofre uma desvalorização de 15% ao ano.
Se v (em reais) é o valor do veículo t anos após sua aquisição,
temos:
v = 40.000 . (1 – 0,15)t \ v = 40.000 . 0,85t
Para que o automóvel perca 80% de seu valor, seu preço de revenda
é igual a 20% de seu preço inicial. Assim:
V = 40.000 . 0,2
40.000 . 0,85t = 40.000 . 0,2
0,85t = 0,2
t = log0,85 0,2
Do gráfico, temos que log0,85 0,2 » 9,5.
Assim, para que o carro perca 80% do seu valor, é necessário que
se passem entre 9 e 10 anos da data da compra do veículo.
Alternativa E
32. Passados 20 anos, o carro valerá cerca de:
a)
b)
c)
d)
e)
R$ 600,00
R$ 1.600,00
R$ 6.000,00
R$ 16.000,00
R$ 25.000,00
Resolução:
Observação: foram utilizadas escalas diferentes nos dois eixos
para facilitar a visualização do gráfico.
Passados 20 anos, o valor v (em reais) do veículo é:
v = 40.000 . 0,8520
Do gráfico: log0,85 0,04 = 20.
Portanto:
0,8520 = 0,04.
Assim:
v = 40.000 . 0,04 = 1600 reais
Alternativa B
INSPERNOV2014
CPV
12
Seu Pé D ireito
INSPER – 02/11/2014
nas
33. Considere que a seguinte afirmação é verdadeira: “Se uma
pessoa é inteligente, então ela tem opiniões bem embasadas
ou está disposta a ouvir os argumentos dos outros.”
Uma pessoa está disposta a ouvir os argumentos dos outros.
Então,
a)
b)
c)
d)
ela é inteligente.
ela tem opiniões bem embasadas.
se ela tiver opiniões bem embasadas, ela é inteligente.
mesmo que tenha opiniões bem embasadas, pode não
ser inteligente.
e) se ela não tiver opiniões bem embasadas, não é
inteligente.
Resolução: Consideremos as proposições:
p: uma pessoa é inteligente;
q: uma pessoa tem opiniões bem embasadas;
r: uma pessoa está disposta a ouvir os argumentos dos outros.
Assim, do enunciado, a afirmação “se p, então r ou q” é verdadeira
e a proposição “r” é verdadeira. Temos:
p
q
r
q ou r
p → (q ou r)
V
V
V
V
V
V
F
V
V
V
F
V
V
V
V
F
F
V
V
V
Nas condições da tabela, mesmo que a pessoa tenha opiniões bem
embasadas (“q” é verdade), pode não ser inteligente (“p” é falsa).
Alternativa D
34. Um determinado micro-organismo tem o seguinte ciclo de
vida:
● 1 dia após ser gerado, produz 2 cópias de si mesmo;
● 2 dias após ser gerado, produz outras 2 cópias de si
mesmo e, imediatamente, morre.
no final do
dia 1
no final do
dia 2
no final do
dia 3
com 1 dia de vida
1
2
6
recém gerados
2
6
16
que acabaram de
morrer
0
1
2
vivos, no total
3
8
22
Passados 6 dias, logo após as gerações e as mortes, a cultura
terá:
a) 46 indivíduos.
c) 564 indivíduos.
e) 2048 indivíduos.
CPV
Resolução:
INSPERNOV2014
b) 448 indivíduos.
d) 1073 indivíduos.
Completando a tabela, temos:
no final do
dia 4
no final do
dia 5
no final do
dia 6
16
44
120
44
120
328
6
16
44
16 + 44 = 60
44 + 120 = 164
120 + 328 = 448
Portanto, a cultura terá 448 indivíduos.
Alternativa B
35. Uma universidade decidiu fazer uma análise sobre a
quantidade de alunos cursando dependências, ou seja, aqueles
que foram reprovados em alguma matéria em determinado
semestre e tiveram de cursá-la novamente no semestre
seguinte. As conclusões, todas referentes a uma mesma
turma de um curso, foram:
● Cerca de 30% dos alunos tiveram dependência em pelo
menos uma matéria ao término do 1o semestre do curso;
● Ao término do 2o semestre, cerca de 80% dos que não
cursavam dependências foram aprovados em todas as
matérias, ao passo que apenas 30% dos que cursavam
alguma dependência foram aprovados em todas as
matérias;
● As mesmas porcentagens do 2o semestre se repetiram
ao final do 3o semestre.
Assim, ao término do 3o semestre, os alunos livres de
dependências para o semestre seguinte representavam:
a) 35,0% da turma.
c) 50,0% da turma.
e) 65,0% da turma.
b) 37,5% da turma.
d) 62,5% da turma.
Resolução:
com dependência
Considere uma cultura que, no início do dia 1, possuía
apenas 1 micro-organismo, imediatamente após ser gerado.
A tabela a seguir mostra a evolução da população ao longo
dos 3 primeiros dias.
Quantidade de
micro-organismos...
Melhores Faculdades
sem dependência
1o S 30%
70%
2o S 20%.70% + 70%.30% = 35%
80%.70% + 30%.30% = 65%
3o S 20%.65% + 70%.35% = 37,5% 80%.65% + 30%.35% = 62,5%
Portanto, ao final do 3o semestre, 62,5% da turma estará livre de
dependências.
Alternativa D
COMENTÁRIO DO CPV
A prova de Análise Quantitativa e Lógica do processo seletivo
do INSPER novembro/2014 manteve suas características,
propondo questões contextualizadas e fazendo uso constante
de gráficos.
A prova mostrou evolução extraordinária em relação às
edições passadas, com o nível de dificuldade mais adequado
ao vestibulando.
Com isso, acreditamos que o objetivo de selecionar os melhores
candidatos seja atingido com mais precisão.