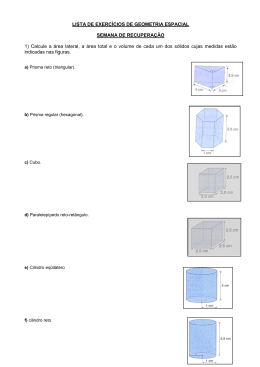
Sólidos Inscritos e Circunscritos
1. (Fuvest 2013) Os vértices de um tetraedro regular são também vértices de um cubo de
aresta 2. A área de uma face desse tetraedro é
a) 2 3
b) 4
c) 3 2
d) 3 3
e) 6
2. (Uerj 2013) Um cristal com a forma de um prisma hexagonal regular, após ser cortado e
polido, deu origem a um sólido de 12 faces triangulares congruentes. Os vértices desse
poliedro são os centros das faces do prisma, conforme representado na figura.
Calcule a razão entre os volumes do sólido e do prisma.
www.nsaulasparticulares.com.br
Página 1 de 10
3. (Ufrn 2013) Por motivo de segurança, construiu-se um superaquário de vidro, em formato
esférico, dentro de um cilindro também de vidro, conforme esquematizado na figura a seguir. A
esfera está completamente cheia de água e, caso quebre, toda a água passará para o cilindro.
Desconsidere a pequena diferença entre os raios da esfera e do cilindro e o volume de água
deslocado pelos pedaços de vidro da esfera quando quebrada. Supondo que R é igual a 2 m,
determine:
a) O volume de água da esfera.
b) A capacidade volumétrica do cilindro.
c) A altura do nível da água no cilindro, caso a esfera quebre.
4. (Udesc 2012) Algumas caixas de pizza para entrega têm o formato de um prisma regular de
base hexagonal. Considere uma caixa destas com altura de 4 cm e, com base, um polígono de
perímetro 72 cm. Se a pizza tem o formato de um cilindro circular, então o volume máximo de
pizza que pode vir nesta caixa é:
a) 216 3 cm3
b) 576π cm3
c) 864 3 cm3
d) 108π cm3
e) 432π cm3
5. (Uff 2010) Em 1596, em sua obra Mysterium Cosmographicum, Johannes Kepler
estabeleceu um modelo do cosmos onde os cinco poliedros regulares são colocados um dentro
do outro, separados por esferas. A ideia de Kepler era relacionar as órbitas dos planetas com
as razões harmônicas dos poliedros regulares.
A razão harmônica de um poliedro regular é a razão entre o raio da esfera circunscrita e o raio
da esfera inscrita no poliedro. A esfera circunscrita a um poliedro regular é aquela que contém
todos os vértices do poliedro. A esfera inscrita, por sua vez, é aquela que é tangente a cada
uma das faces do poliedro.
A razão harmônica de qualquer cubo é igual a:
a) 1
b) 2
c)
2
d)
3
www.nsaulasparticulares.com.br
e)
3
2
Página 2 de 10
6. (Ufscar 2010) A figura mostra um prisma retangular reto de base quadrada com um cilindro
circular reto inscrito no prisma. O lado da base do prisma mede 4 dm e a altura é dada por h(x)
= x3 – 5x2 + 8x dm, com x > 0.
a) Calcule o volume do prisma para x = 3 dm.
b) Para x = 1 dm o volume do cilindro inscrito é 16  dm3. Encontre os outros valores de x para
os quais isto acontece.
7. (Uerj 2010) Uma embalagem em forma de prisma octogonal regular contém uma pizza
circular que tangencia as faces do prisma.
Desprezando a espessura da pizza e do material usado na embalagem, a razão entre a medida
do raio da pizza e a medida da aresta da base do prisma é igual a:
a) 2 2
3 2
4
2 1
c)
2
d) 2 2  1
b)


8. (Fgv 2009) Considere uma pirâmide regular de altura
3 6
cuja base é um quadrado de lado
2
3. Calcule:
a) o volume da pirâmide.
b) o raio da esfera circunscrita à pirâmide.
www.nsaulasparticulares.com.br
Página 3 de 10
9. (Puc-rio 2009) Um cilindro reto de base circular de raio r e altura h é inscrito numa esfera
de raio 5.
a) Encontre a altura do cilindro quando r = 3.
b) Calcule a área total do cilindro quando r = 3.
c) Escreva a área total do cilindro como função de r.
10. (Uerj 2009) A figura a seguir representa uma caixa, com a forma de um prisma triangular
regular, contendo uma bola perfeitamente esférica que tangencia internamente as cinco faces
do prisma.
Admitindo π= 3, determine o valor aproximado da porcentagem ocupada pelo volume da bola
em relação ao volume da caixa.
11. (Unesp 2008) Um porta-canetas tem a forma de um cilindro circular reto de 12 cm de altura
e 5 cm de raio. Sua parte interna é um prisma regular de base triangular, como ilustrado na
figura, onde o triângulo e equilátero e está inscrito na circunferência.
A região entre o prisma e o cilindro é fechada e não aproveitável. Determine o volume dessa
região. Para os cálculos finais, considere as aproximações π = 3 e
www.nsaulasparticulares.com.br
3 = 1,7.
Página 4 de 10
12. (Ueg 2008) Um fabricante de bolas deseja adquirir uma caixa de forma cúbica para
acondicionar uma bola de volume Vb. A razão entre os volumes dessa bola e do menor cubo
possível para acondicioná-la é:
a) π/4
b) π/5
c) π/3
d) π/6
13. (Ufmg 2007) Nesta figura, estão representados o cubo ABCDEFGH e o sólido OPQRST:
Cada aresta do cubo mede 4 cm e os vértices do sólido OPQRST são os pontos centrais das
faces do cubo. Então, é correto afirmar que a área lateral total do sólido OPQRST mede
a) 8 2 cm2.
b) 8 3 cm2.
c) 16 2 cm2.
d) 16 3 cm2.
14. (Puc-rio 2007) Seja E uma esfera de raio 1 metro. Considere dois cubos, um contido em E,
de maior volume possível e outro que contém E, de menor volume possível. Ache a razão entre
os volumes dos dois cubos.
15. (Ufu 2007) Calcule a medida da diagonal de um cubo circunscrito a uma esfera de volume
36π cm3.
16. (Fuvest 2006) Um cone circular reto está inscrito em um paralelepípedo reto retângulo, de
base quadrada, como mostra a figura. A razão b/a entre as dimensões do paralelepípedo é
3
2
e o volume do cone é π.
Então, o comprimento g da geratriz do cone é
a)
5
b)
6
c)
7
www.nsaulasparticulares.com.br
d)
10
e)
11
Página 5 de 10
17. (Pucsp 2006) De um cristal de rocha, com o formato de uma esfera, foi lapidada uma joia
na forma de um octaedro regular, como mostra a figura seguinte.
Se tal joia tem 9 2 cm3 de volume, quantos centímetros cúbicos de rocha foram retirados do
cristal original para lapidá-la? (Use: π = 3)
a) 36 2
b) 32 2
c) 24 2
d) 18 2
e) 12 2
18. (Ufrrj 2005) Em uma caixa d'água cúbica vazia de lado 2m, é colocada, cheia de água,
uma esfera inscrita, com espessura da parede desprezível. Estoura-se a esfera e retiram-se
seus resíduos. Qual a altura de água que permanecerá dentro da caixa?
19. (Ufrn 2004) Um artista esculpiu a metade de uma esfera de pedra-sabão, transformando-a
num cone, ilustrado na figura a seguir.
Supondo que a esfera tem raio R e a altura do cone esculpido também é R, calcule:
a) o volume do cone esculpido;
b) o volume do material retirado da metade da esfera para formar o cone.
20. (Ufsm 2000) Bolas de tênis são vendidas, normalmente, em embalagens cilíndricas
contendo 3 unidades.
Supondo-se que as bolas têm raio a em centímetros e tangenciam as paredes internas da
embalagem, o espaço interno dessa embalagem que NÃO é ocupado pelas bolas é, em cm3
a) 2πa3
b)
(4πa3 )
3
c)
( πa3 )
3
d) a3
e)
www.nsaulasparticulares.com.br
(2πa3 )
3
Página 6 de 10
Gabarito:
Resposta da questão 1:
[A]
Considere a figura.
Como qualquer uma das faces do tetraedro VABC é um triângulo equilátero de lado 2 2,
segue que a área pedida é dada por
(2 2)2  3
 2 3 u.a.
4
Resposta
da
questão
Sendo 2 a medida da aresta da base do prisma, considere a seguinte vista superior.
2:
Aplicando a Lei dos Cossenos no triângulo ABC, obtemos
x2 
2

2
 2    cos120  x 2  2
x
2
2
2
 1
 
 2
3,
em que x é a medida da aresta da base das pirâmides hexagonais regulares obtidas pelo corte.
Portanto, se h é a altura do prisma, segue que a razão pedida é dada por
2
1 3  ( 3)2 h


3
2
2  1.
2
4
3  (2 )
h
2
www.nsaulasparticulares.com.br
Página 7 de 10
Resposta da questão 3:
a) O volume de água na esfera é dado por
4
4
32
πR3  π  23 
π m3 .
3
3
3
b) Como o cilindro é equilátero, segue que sua capacidade volumétrica é dada por
2πR3  2π  23  16π m3 .
c) A altura h do nível da água no cilindro, caso a esfera quebre é tal que
32
8
π  22  h 
 π  h  m.
3
3
Resposta da questão 4:
[E]
Como o perímetro da base do prisma é igual a 72 cm, segue que a aresta da base desse
72
 12cm. Portanto, sabendo que o raio do cilindro é igual
prisma mede 
6
3 12 3

 6 3 cm e a altura da caixa é 4 cm, temos que o volume máximo de pizza que
2
2
pode vir na caixa é π  (6 3)2  4  432π cm3 .
Resposta da questão 5:
[D]
r
a
a 3
e R
2
2
R

r
a 3
2 =a 3
a
22
Resposta da questão 6:
a) Seja V(x)  42  h(x) o volume do prisma.
Para x  3dm, temos:
V(3)  16  (33  5  32  8  3)  16  6  96dm3 .
b) Seja VC (x)  r 2  h(x) o volume do cilindro circular reto de raio
4
  2dm.
2 2
Se VC (x)  16 dm3, então
r
 22  (x3  5x2  8x)  16  x3  5x2  8x  4  0.
Logo, x  1 é raiz de x3  5x2  8x  4  0.
Aplicando o dispositivo de Briot-Ruffini, obtemos:
1 1 5 8 4
1 4 4 0
www.nsaulasparticulares.com.br
Página 8 de 10
Donde
x3  5x2  8x  4  (x  1)  (x2  4x  4)  (x  1)  (x  2)2  0,
isto é, x  2 é raiz de x3  5x2  8x  4  0 e, portanto, VC (x)  16 dm3 também para
x  2dm.
Resposta da questão 7:
[C]
Sejam O, A e M, respectivamente, o centro da pizza, um vértice do prisma e o ponto médio de
uma das arestas adjacentes ao vértice A.
Queremos calcular
OM
.
2  MA
ˆ  180  2230'.
MOA
8
ˆ
tgMOA  tg2230'

1  cos 45
1  cos 45
2
2
2  2  2  (2  2)  2  2  2  1.

2
2
2 2
2
1
2
1
ˆ  MA  2  1  MA
tgMOA
OM
OM

OM
1
2 1


 2  1.
MA
2 1 2 1
Portanto,
OM 1 OM
2 1
 

.
2
2MA 2 MA
Resposta da questão 8:
a)
b)
9 6
u.v.
2
6 u.c.
www.nsaulasparticulares.com.br
Página 9 de 10
Resposta da questão 9:
a) 8u.c.
b) 66π u.a.


c) 2πr r  2
 25  r   u.a.
2
Resposta da questão 10:
38%
Resposta da questão 11:
517,5 cm3
Resposta da questão 12:
[D]
Resposta da questão 13:
[D]
Resposta da questão 14:
3 3
Resposta da questão 15:
6 3 cm
Resposta da questão 16:
[D]
Resposta da questão 17:
[D]
Resposta da questão 18:
h = π/3 m
Resposta da questão 19:
a)
πR 3
3
b)
πR 3
3
Resposta da questão 20:
[A]
www.nsaulasparticulares.com.br
Página 10 de 10