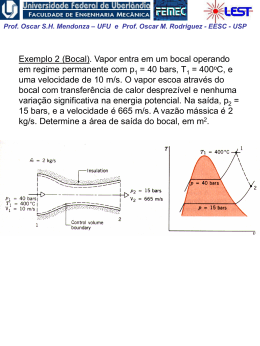
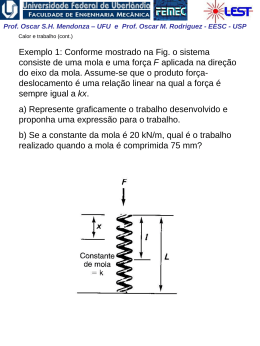
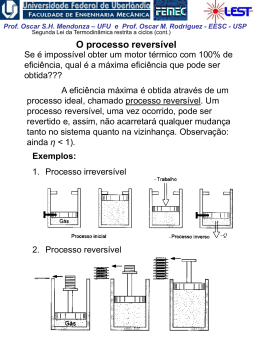
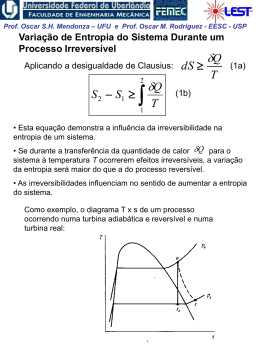
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Variação de Entropia em Processos
Reversíveis
Q 
s2  s1   

T
rev.
1
2
Podemos constatar que, se o processo é reversível e
adiabático
 ds q 0  0
Para processos reversíveis:
 q  T .ds
Portanto, o calor num diagrama T-s pode ser visualizado,
como a área abaixo de um processo reversível.
2
T
ve
rs
ív
el
T
re
q=Tds
1
ds
s
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Façamos uma análise restrita a:
1. Processo reversível
2. Motor térmico
3. Ciclo de Carnot
1. dois processos isotérmicos reversíveis
2. dois processos adiabáticos reversíveis
Ciclo de Carnot no diagrama Temperatura Entropia (T x S):
W
QL
O rendimento do ciclo pode ser expresso em termos de
áreas:
 térmico 
Wlíq
QH
área 1 - 2 - 3 - 4 - 1

área 1 - 2 - b - a - 1
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Processos:
•
1-2, transferência de calor positiva isotérmica (do
reservatório de alta temperatura, TH, para o fluido de
trabalho)
2
2
Q 
1

S 2  S1  
 
 T  rev TH
1
Q2
Q 
TH
1


1
a entropia do sistema aumenta.
•
2-3, processo adiabático reversível
dS 

 Q   0


 T  rev
o processo é adiabático, portanto a entropia permanece
constante. Este é um processo isoentrópico e a temperatura
do fluido de trabalho atinge TL
•
3-4, transferência de calor negativa isotérmica (do
fluido de trabalho para o reservatório de baixa
temperatura, TH.
4
S 4  S3 
 Q   1


 T  rev TL
3

2

1
Q 
Q4
TL
3
a entropia do sistema diminui.
•
4-1, processo adiabático reversível, e portanto
isoentrópico
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Considerando os processos reversíveis de transferência
de calor, analisamos um processo 1-2 de mudança de
estado de líquido para vapor saturado no diagrama T x s:
Como trata-se de um processo a pressão constante, da
definição de entalpia, o calor transferido por unidade de
massa é igual a hlv , assim:
2
2
hlv
1  Q 
1
1 q2
s2  s1  slv 
Q 


 
m 1 T 
mT 1
T
T
rev


Obs.: verifique nas tabelas termodinâmicas a relação entre a
variação da entropia e variação da entalpia descrita acima.
Se continuamos transferindo calor a pressão constante ao
vapor saturado, temos:
3

3

1
Q  Tds
2 q3 
m2
2
mas:
2
É necessário
conhecer a relação
entre T e s, pois T
não é cte.
q3  área 2 - 3 - c - b - 2
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Exemplo 1:
Água inicialmente como líquido saturado a 100oC está
contida num conjunto êmbolo-cilindro. A água realiza um
processo ao estado correspondente de vapor saturado,
durante o qual o êmbolo move-se livremente no cilindro.
Se a mudança de estado ocorre através do aquecimento
da água num processo internamente reversível a pressão
e temperatura constantes, determine o trabalho e a
transferência de calor por unidade de massa, ambos em
kJ/kg.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Duas relações termodinâmicas importantes
Equações de Gibbs:
TdS  dU  pdV
TdS  dH  Vdp
1a Lei : Q  dU  W

(1) Q  TdS
W  pdV

(2)
 H  U  pV

dH  dU  pdV  Vdp
substitui- se em (1)

A integração deve ser realizada ao longo de um caminho
reversível, porém as equações de Gibbs podem ser
aplicadas a um processo irreversível, pois lida-se
apenas com propriedades termodinâmicas.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Variação de entropia de um gás perfeito
Da 1ª equação de Gibbs:
Tds  du  pdv
Para um gás perfeito:
du  cvo dT
e
RT
p
v
Assim:
dT Rdv
ds  cvo

T
v
Integrando:
2
dT
 v2 
s2  s1  cvo
 R ln 
T
 v1 
1

Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Analogamente, da 2ª equação de Gibbs:
Tds  dh  vdp
Para um gás perfeito:
RT
dh  c po dT e v 
p
Assim:
ds  c po
dT Rdp

T
p
Integrando:
2

s2  s1  c po
1
dT
 p2 
 R ln 
T
 p1 
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Para integrar as equações acima, devemos conhecer
as relações entre calores específicos e a temperatura.
1- Calores específicos constantes:
 T2 
 p2 
s2  s1  c po ln   R ln 
 T1 
 p1 
e
 T2 
 v2 
s2  s1  cvo ln   R ln 
 T1 
 v1 
2- Equações ajustadas empiricamente para cpo (Tab. A.6):
3- Integração dos cálculos da termodinâmica estatística
(Tabs. A.7 e A.8):
T
s 
o
T
Assim
c po
 T dT
To
 p2 
s2  s1  s  s   R ln 
 p1 
o
T2
(+)
o
T1
Portanto, temos três possibilidades para avaliar c po :
3- Tabelas de gás ideal
2- Equações empíricas
precisão
(-)
1- Calor específico constante
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Processo politrópico reversível para gás perfeito
Para processo reversível, adiabático, i.e., isoentrópico,
com cpo = cte:
ou
 T2 
 p2 
s2  s1  0  c po ln   R ln 
 T1 
 p1 
 T2  R  p2 
ln  
ln 
 T1  c po  p1 
e
T2  p2 
 
T1  p1 
mas:
R
c po
c po  cvo k  1
R


c po
c po
k
onde:
k
Assim:
T2  p2 
  
T1  p1 
k 1
k
pvk  cte.
c po
cvo
T2  v1 
 
T1  v2 
k 1
p2  v1 
 
p1  v2 
k
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Relembrando que para processo politrópico de
gás ideal:
pV n  cte.
ou
p2  V1 
 
p1  V2 
e
 n 1 / n
T2  p2 
 
T1  p1 
e
W 
2

1
2
W 

1
n
 V1 
 
 V2 
n 1
mR T2  T1  n  1
pd V 
1 n
V2
n  1
pd V  mRT ln
V1
Portanto:
• Processo isotérmico (T = cte.):
• Processo isobárico (p = cte.):
• Processo isocórico (v = cte.):
• Processo isoentrópico (s = cte.):
pv = cte; n = 1
pv0 = cte; n = 0
pvºº = cte; n = ∞
pvk = cte; n = k
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Exemplo 2
Ar realiza um processo isentrópico de p1 = 1 bar, T1 = 300
K até um estado final onde a temperatura é T2 = 650 K.
Empregando o modelo do gás ideal, determine a pressão
final p2, em bar. Resolva usando (a) dados de da tabela
sT0
A.7 (van Wylen, 6a ed.) e (b) razão de calores específicos
constante, k avaliada na temperatura ambiente (Tab.
A.5).