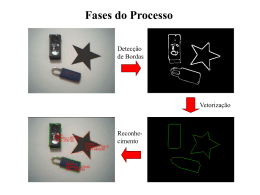
Visão Computacional
Features (características)
http://www.dca.ufrn.br/~lmarcos/courses/visao
Sinopse
• Conceito de features
• Arestas, contornos, curvas
• Features não geométricas
•
O que são features?
• Feature global
– Uma propriedade global de uma imagem ou
parte dela, por exemplo, média dos níveis de
cinza, área em pixel.
• Feature local
– Parte de uma imagem com propriedades
especiais, por exemplo, um círculo, uma linha,
ou uma região com textura numa imagem de
intensidade, uma superfície plana numa
imagem de profundidade
Definição
• Features (características) de imagem são
partes detectáveis locais da imagem com
algum significado (meaningful)
• Seqüência de operações iniciais dos
sistemas de visão:
– Detecção (realce) de features
– Localização de features
Significado (meaningful)
• Associadas a elementos de interesse na cena
via o processo de formação de imagens
– Variação alta da intensidade causada pelos
contornos
– Regiões com nível de intensidade uniforme
– Algumas vezes procuramos features que não se
traduzem a alguma característica na imagem
mas refletem arranjos particulares dos pixels
com certas propriedades desejadas (invariância,
coisas fáceis de detectar).
Detectáveis
• Deve existir um algoritmo de localização,
caso contrário, a feature não serve para nada
• Features diferentes são associadas a
algoritmos de detecção diferentes;
• A saída geralmente são os descritores das
features, especificando posição e outras
propriedades essenciais da feature.
– Ex: descritor de linha contém o ponto central,
seu tamanho e orientação.
Arestas (bordas)
• São pixels (ou regiões) da imagem onde o
valor da intensidade possui uma variação
brusca
• Problema de detecção de arestas:
– dada uma imagem (considere com erro),
localizar as arestas geradas pelos elementos da
cena (não pelo erro)
Por que aresta interessa?
• Contornos de elementos de interesse na
cena
– objetos sólidos, marcas em superfícies, sombras
– Linhas, curvas e contornos (elementos básicos
para muitos algoritmos) são cadeias de pixels
de arestas
– Line drawing (wire frame) é são imagens
comuns e sugestivas para seres humanos
Algoritmo
• Suavização do ruído
– suprimir ruídos sem destruir arestas
– assumir ruído branco ou gaussiano
• Realce de arestas
– projetar um filtro que responda a arestas
– valor alto nas arestas e baixo fora delas
• Localização de arestas
– decidir que máximos locais no filtro são arestas
• afinar arestas grossas para um pixel de largura
• estabelecer um valor mínimo para aresta (treshold)
Detetor de arestas de Canny
• Seja f(x,y) uma imagem, com ruído branco
ou gaussiano
• Para eliminar (ou diminuir) ruído, convoluir
com o filtro gaussiano
Gaussiano
Espaço
Freqüência
Gradiente do Gaussiano
Espaço
Freqüência
Laplaciano do Gaussiano
Espaço
Freqüência
Canny
• Então f*g suprime erro antes da detecção de
arestas, ou seja, limita f em banda, mas
ainda é uma boa aproximação de f
• Então, para detectar arestas, basta aplicar
diferenciação
Canny
• Como o filtro gaussiano é linear, leva-se a
diferenciação para a máscara da gaussiana e
então aplica-se o resultado (outra máscara)
à imagem original.
• O resultado é o mesmo que se fosse
primeiro suavizado e depois diferenciado.
Algoritmo de Canny
• Aplicar CannyEnhancer a I(i,j)
• Aplicar NonMaxSuppression ao resultado
• Aplicar HysteresisThresh ao resultado
Função CannyEnhancer
• Aplicar suavização gaussiana a I(i,j) (filtro
linear com kernel gaussiano discretizado)
J=I*G
• Para cada pixel (i,j):
– a) calcule as componentes do gradiente Jy e Jx
– b) estime a magnitude da aresta (strenght)
Es(i,j)=(Jx2(i,j)+Jy2(i,j))1/2
– c) estime a orientação da normal da aresta
E(i,j)=atan2(Jy,Jx)
Função NonMaxSuppresion
• Considere as direções dk = 0, 45, 90, 135o
• Para cada pixel em es(i,j)
– ache a direção dk que melhor aproxima a
direção de E(i,j) (a normal à aresta)
– se Es(i,j) for menor que pelo menos um dos dois
vizinhos ao longo de dk faça In(i,j)=0
(supressão); caso contrário, faça In(i,j)= Es(i,j)
• Saída é imagem In(i,j) de pontos de arestas
afinadas, isto é, Es(i,j) após supressão de
pontos de aresta não máximos (max. locais)
Eliminando máximos locais
(tresholding)
• A imagem afinada ainda contém máximos
locais criados por erro
• Uma idéia seria descartar pixels com
valores menor que um treshold. Problemas:
– se tentarmos capturar arestas verdadeiras que
sejam fracas, algum erro pode ainda passar
(contornos falsos)
– os valores dos máximos verdadeiros podem
flutuar ao longo de uma aresta, acima e abaixo
do treshold, fragmentando a aresta resultante.
Função HysteresisTresh
• Entrada é a imagem In(i,j), E(i,j) e l e h,
dois tresholds l<h
• Para todos os pontos em In(i,j), passando
numa ordem fixa:
– localiza próximo pixel não visitado In(i,j) > h
– começando de In(i,j), tente achar uma cadeia de
máximos locais conectados em ambas as
direções perpendiculares à normal à aresta
desde que In(i,j) > l.
– Marque todos os pontos visitados e salve a lista
das posições dos pixels no contorno conectado
encontrado.
Saída do algoritmo
• Conjunto de listas de arestas, cada uma
descrevendo a posição de um contorno
conectado na imagem
• Imagem de orientação
• Imagem de magnitude
Generalidades
• Hysteresis reduz probabilidade de falsos
contornos, uma vez que estes devem
produzir uma resposta maior que h para
ocorrerem
• Reduz probabilidade de quebra, requerendo
flutuações muito maiores que no caso de
simples thresholding
• Tracking de arestas, achando máximos em
arestas conectados, ou contornos conectados
Algoritmo RobertsEdgeDetector
(Input: imagem I(i,j) e treshold )
• Aplique remoção de ruídos caso deseje (Is)
• filtrar Is(i,j) com as máscaras de roberts
1-1
-1 1
-1 1
1-1
obtendo duas imagens I1(i,j) e I2(i,j)
• estime a magnitude do gradiente em cada
pixel como
G(i,j)=(I12(i,j)+I22(i,j))1/2
• marque como aresta todos o pixels em que
G(i,j)>.
Algoritmo SobelEdgeDetector
• Mesmo que Roberts, exceto as máscaras do
segundo passo
• Prewitt: similar
Detectando cantos
• Considere o gradiente espacial da imagem
dado por (Ex,Ey)t , com Ex=E/x e
Ey=E/y;
• Considere um pixel p genérico na imagem,
uma vizinhança Q de p e uma matriz C:
Ex2 ExEy
C=
ExEy Ey2
onde as somatórias são tomadas sobre a
vizinhança Q.
• A matriz C caracteriza a estrutura dos níveis
de cinza da imagem, em cada pixel.
Auto-valores e auto-vetores
• A matriz C é simétrica, portanto pode ser
diagonalizada por uma rotação do eixo de
coordenadas, sem perda de generalidades:
1 0
C=
0
2
Os dois auto-valores 1 e 2 são não negativos
(assumamos 1 > 2).
Interpret. geométrica de 1 e 2
• 1) Considere uma vizinhança Q uniforme: o
gradiente desaparece em toda a vizinhança,
C vira uma matriz nula e 1=2=0
• 2) Assuma que Q contém um aresta degrau
ideal preto para branco; temos então 2=0,
1>0 e o auto-vetor associado com 1 é
paralelo ao gradiente da imagem
• O posto (rank) de C é deficiente nos dois
casos (0 e 1, respectivamente).
Interpret. geométrica de 1 e 2
• 3) Considere que Q contém o canto de um
quadrado preto contra um fundo branco:
como tem duas direções principais em Q,
espera-se que 1>2>0 e que quanto maior
forem, mais forte (maior contraste) serão as
linhas da imagem correspondente
• Posto de C é 2
Interpret. geométrica de 1 e 2
• Auto-vetores codificam direções das arestas
e auto-valores codificam sua magnitude.
• Um canto é identificado por duas arestas
fortes, então sendo 1>2, um canto é uma
localização onde o menor deles é grande
Algoritmo Corners
(Input: I(x,y), threshold 2,  e tamanho de Q)
• Calcule o gradiente na imagem I(x,y)
• Para cada pixel p:
– a) componha a matriz C numa vizinhança 2n+1
– b) calcule 2, o menor dos auto-valores de C
– c) se 2>, salve coordenadas de p numa lista L
• Ordene L em ordem decrescente de 2
• Passando na lista (ordenada), para cada
ponto corrente p, apague todos os pontos
que aparecem depois na lista mas que
pertençam também à vizinhança de p.
Generalidades
• O threshold  pode ser estimado a partir do
histograma de 2.
• O tamanho da vizinhança Q não é trivial,
não havendo um critério para sua definição.
• Experiências indicam um tamanho entre 2 e
10 como sendo adequado na maioria dos
casos práticos
Operadores de textura Frei e Chen
• A probabilidade de operadores de aresta
encontrarem uma evidência zero de uma
aresta em qualquer lugar da imagem é muito
pequena, devido ao ruído superposto em
variações de baixa freqüência
• Algumas vezes, gradiente não funciona
como esperado
Operadores de Frei e Chen
• Considere o conjunto de operadores:
Operadores de Frei e Chen
• Seja gk = f * hk, então:
• Definindo
• Se >threshold, reporte/rotule aresta
Magnitude do gradiente
x
Threshold de Frei-Chen
Detecção de linhas e curvas
• Dada a saída de um operador de arestas,
encontrar todas as instâncias de uma dada
curva (linha ou elipse) ou parte dela
(segmentos de linha ou arcos de elipses)
• Agrupamento
– Quais pontos da imagem compõem cada
instância da curva alvo na imagem
• Model fitting
– Dado um conjunto de pontos na imagem
provavelmente pertencente a uma instância
única da curva alvo, encontrar a melhor curva
que interpola os pontos
Transformada de Hough (linhas)
• Transforma detecção de linhas em um
problema de interseção de linhas
• Qualquer linha y=mx+n é identificada por
um par (m,n), representada por um ponto no
plano (m,n) , o espaço de parâmetros
• Por outro lado, qualquer ponto p=(x,y) na
imagem corresponde a uma linha n=-mx+y
no espaço de parâmetros
• Variando (m,n), pode-se representar todas as
linhas possíveis que passam em p
Transformada de Hough (linhas)
• Uma linha definida por k pixels colineares
p1,...pk, é identificada no espaço de
parâmetros pela interseção das linhas
associadas a p1,...,pk
n
x
p2
p1
n
m=tan 

y
m
Transformada de Hough (linhas)
• Basta transformar interseção de linhas em
um problema de detecção de pico,
procurando por um máximo de interseções
• Dividir o plano (m,n) numa grade discreta
(resolução depende da precisão desejada)
• Associar um contador a cada célula,
inicialmente zero para todas
Exemplo
• Seja apenas uma linha (m´,n´) na imagem,
formada pelos pontos p1,...,pk
• Para cada pixel pi, incremente todos os
contadores na linha correspondente no
espaço de parâmetros
• Todas as linhas r1,...,rk no espaço de
parâmetros associadas a p1,...,pk terão os
mesmos parâmetros (m´, n´), de modo que
c(m´,n´) = k e os contadores das outras
linhas são 1.
• Basta então achar o pico de c(m,n)
Na prática
n=-mx+y
y=mx+n
y
2
n
m=1
n=0
1
1
2
x
1
x=1
y=1
1
n=-m+1
m=0, n=1
m=1,n=0
x=2
y=2
n=-2m+2
m=0, n=2
m=1,n=0
m
Problemas com m e n
• Como manter m e n (que são infinitos)
dentro de uma resolução desejada
(discreto), de modo a não perder linhas?
• O par (m,n) não captura a linha x=c (com c
constante)
Representação polar
• Usar representação polar: =x cos+y sin,
onde  representa a distância entre a origem
da imagem e a linha e  a sua orientação
• Os parâmetros  e  são finitos e podem
representar qualquer linha
x
x
p2
p1

n
m=tan 

y
p2
p1
=x cos+y sin

y
Detecção de várias linhas
• Arestas na imagem podem ter varias linhas
• Encontrar todas: olhar para todos os
máximos locais em c(m,n)
• Pontos em curvas ou ruídos geram pontos
randômicos no espaço (m,n).
• Basta passar um threshold
• Ruídos
Algoritmo HoughLines
Input: E(i,j), d<=(M2+N2)1/2,d [0,] e R,T
• Discretize espaço de parâmetros de  e 
nos vetores d e d usando passos  e 
• Seja A(R,T) matriz de contadores,em zero
• Para cada pixel E(i,j)=1, e para h=1,...,T
– faça =i cosd(h)+j sind(h)
– ache o índice k, do elemento de d mais
próximo de 
– incremente A(k,h)
• Encontre todos os máximos locais (kp,hp),
tais A(kp,hp)>, trhreshold def. pelo usuário
HoughCurves
Input: Seja f(x,a) parametrizacao da curva
• Discretize os intervalos de variação de a1, ..., ap.
Sejam s1, ..., sp os tamanhos dos intervalos
amostrados
• Seja A(s1, ..., sp) um vetor de contadores inteiros,
inicialmente em zero
• Para cada pixel E(i,j)=1, incremente todos os
contadores na curva definida por y=f(x,a) em A
• Encontre todos os máximos locais am tais que
A(am)>, o trhreshold definido pelo usuário
Homework
• Implemente os algoritmos de deteção de arestas de
Sobel, Prewit, Roberts, Chen e Frei.
• Implemente o algoritmo de detecção de cantos do
livro do Trucco.
• Implemente os filtros Gaussiano, Gradiente do
Gaussiano e Laplaciano do Gaussiano.
• Teste a transformada de hough para linhas (use
uma implementação já existente).
• Faça um relatório, iincluindo as máscaras usadas
de cada filtro, bem como as imagens resultantes.
Comente os resultados.