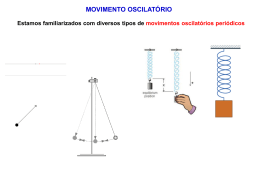
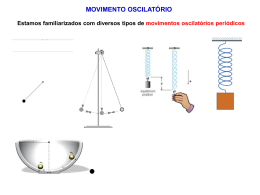
Suspensão do Fusca era por Barra de Torção
Os efeitos da dinâmica e da cinemática
de rotações será estudada no caso da
torção de um fio metálico.
Assume-se como modelo matemático
para a descrição destas torções a lei
de Hooke  F = - kx
Como modelo matemático para o atrito viscoso
assume-se que seja proporcional a velocidade
angular.
Elementos básicos do experimento.
Ponteiro, disco suspenso por fio metálico e recipiente com líquido o viscoso.
Não deixe balançar!
Modo correto!
CÁLCULO DO MOMENTO DE INÉRCIA DO DISCO, PINO E COPO.
I DISCO
1
 MR 2
2
I PinoCentral
I COPO
1
 MR 2
2
1
2
2
 M(R 2  R1 )
2
http://faraday.physics.utoronto.ca/IYearLab/Intros/TorsionPend/TorsionPend.html
Torque.
Torque de um disco.
dLz
d 
z 
I 2
dt
dt
2
Torque do fio.
fio
z
 k
Procedimentos de medida do pino, disco e copo.
Para pequenas oscilações vale a lei de Hooke  F = -k x
Neste caso o atrito viscoso é com o ar e será desprezado.
Click aqui!
I  k
Robert Hooke
 ( t )   max cos(0 t )
0 
k
I
Freqüência angular para oscilações livres.
Solução da equação do movimento:
I   k  I
d 2 ( t )
( t )  A cos(t )
dt
2
  k ( t )
Vamos testar uma solução com a função cosseno!
d(t )
 Asen(t )
dt
d ( t )
2
dt2
Derivamos a função cosseno.
 A2 cos(t )
Substituimos na equação:
Obtemos a relação:
 IA2 cos(t )  kAcos(t )
I2  k
Para t=0 a constante A =max
A solução final será:
k
( t )   max cos( t )
I
Medida da constante elástica do fio.
Freqüência angular com dissipação desprezível.
2
0 

T0
k
I
Propagação dos erros na determinação de k.
  I    T0
 k  k    2
 I   T0
2




2
Oscilações livres com amortecimento viscoso proporcional a velocidade angular.
Torque da força viscosa
visc.
z
d
 b
dt



I  b  k

b
é o atrito viscoso.
2I
 (t )   maxe
t
cos(1t )
Freqüência angular com dissipação viscosa.
2
k b
1 

 
T1
I  2I 
2
Solução da Equação do Movimento com Atrito Viscoso
I   b  k  I
d 2 ( t )
dt 2
d( t )
 b
 k( t )
dt
(t )  Aext
Vamos testar uma solução com a função:
As suas respectivas derivadas são:
Que, substituídas na equação resulta:
Ix  bx  k  0
2
d(t )
 Axext
dt
d 2 ( t )
2 xt

Ax
e
2
dt
IAx2 e xt  bAxext  kAext
2
a solução para x será:
b
k
b
x    
2I
I
 2I 
2
A solução fica na forma: 
b
 b  k
    
I
 2I  2I 

( t )  Ae


t


Observe que temos duas
soluções possíveis!
2
k
 b 
Mas! 
então o termo da raiz é complexo!
 é muito menor que
I
 2I 

 k  b 2
b   i I  2 I 
 


Ae 2 I e 
Escrevendo a raiz na forma:
( t ) 

Uma solução parcial será:
(t )  Ae


t


e fazendo:
1 
b
 ei1t
2I 


k  b
 
I  2I 
 e i1t
2




2
Usando-se a relação de Euler:
ei1t  e i1t
cos1t 
2
A solução final tem a forma:
(t )  maxe  cos(1t )
O termo de atrito viscoso é:
b

2I
A freqüência angular desta oscilação será:
1 
k  b
 
I  2I 
2
Obs.: Algumas aproximações e simplificações na busca da solução
da equação do movimento com atrito viscoso foram feitas e devem
ser discutidas com o seu professor de teoria.
Lembre-se! Aqui a função exponencial descreve apenas a dissipação do sistema.
Observe que:A função exponencial desloca o máximo da função cosseno.
e-(t)
e-(t)cos(t)
cos(t)
Determinação de gama por gráfico mono-log.
  2
1
2
T0

1
2
T1
Determinação de gama
por gráfico mono-log.
 (t )   maxe
loge  (t )  loge ( maxe
t
t
cos(1t )
cos(1t ) )



desconsiderar
loge  ( t )  t  loge  max
loge  ( t )  a  t
Não esquecer barra de erro!
A energia mecânica quando conservada pode ser escrita como:
1
1  d (t )  1 2
2
E  k (t )  I 
  k max
2
2  dt 
2
2
A energia mecânica no caso amortecido não é conservada:
 (t )   maxe
t
cos(1t )
Assim a energia mecânica não é constante ao longo do tempo mas
a energia mecânica média num período sim.
Podemos defini-la pela expressão:
1
E (t ) 
T1

t T1
t
E (t )dt
Resultando:
1 2
2t
2t
E(t )  k max.e
 E0e
2
Revendo o caso não amortecido e amortecido crítico.
 ( t )   max cos(0 t )
0 
b

2I
2

T0
k
I
 (t )   maxe t cos(1t)
2
k b
1 

 
T1
I  2I 
2
Este Experimento é composto de 11 procedimentos:
1) Medida do período não amortecido.
2) Medida dos pontos de inversão, caso não amortecido.
3) Gráfico deste movimento de oscilação em função do tempo.
4) Cálculo geométrico do momento de inércia total.
5)Determinação do k de torção elástica do fio.
6) Medida do período T1 , caso amortecido.
7) Determinação de   b/2I.
8) Medida dos pontos de inversão, caso amortecido.
9) Gráfico deste movimento de oscilação em função do tempo.
10) Análise da curva envoltória, caso amortecido.
11) Estudo da dissipação de energia, caso amortecido.
Prof. Dr. Hélio Dias – [email protected]
Sebastião Simionatto – 2010
[email protected]