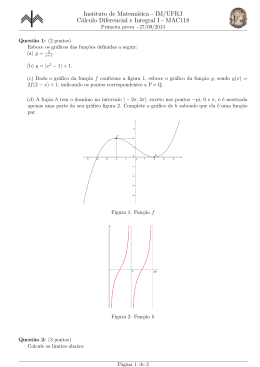
Limites e Continuidade de Funções Reais de
Uma Variável Real
Carla Montorfano
João César Guirado
João Roberto Gerônimo
Jorge Ferreira Lacerda
Rui Marcos de Oliveira Barros
Valdeni Soliani Franco
Apresentação
O propósito deste texto é apresentar, de maneira concisa, conceitos e resultados do Cálculo
Diferencial e Integral. Aqui serão estudados limites e continuidade de funções reais de uma variável real e
suas principais propriedades. O texto está escrito em linguagem precisa e esclarecedora. Precisa, porque a
Matemática não pode ser construída sem o devido rigor, na linguagem e na lógica de suas proposições;
esclarecedora, porque desejamos evitar o aparecimento de definições e nomenclaturas desnecessárias, que
dificultem o caminhar do estudante durante a leitura desta obra.
Este é o segundo de uma série de quatro volumes que tratarão dos seguintes assuntos: conjuntos
numéricos e funções; limites e continuidade; derivadas e aplicações; integrais e aplicações.
Visando a complementação dos textos, será criada uma página na Internet, na qual serão
apresentados exemplos adicionais, biografias, fatos históricos e curiosidades inerentes ao Cálculo, bem como
serão propostos mais exercícios e bibliografias, para permitir ao estudante aprofundar seus estudos em nível
de graduação.
Sumário
Limites ................................................................................................................................................................. 4
Definição de Limite ...................................................................................................................................... 7
Propriedades dos Limites...........................................................................................................................13
Limites Infinitos...............................................................................................................................................20
Propriedades dos Limites Infinitos ..........................................................................................................23
Limites no Infinito ..........................................................................................................................................25
Assíntotas ..........................................................................................................................................................28
Assíntota Vertical ........................................................................................................................................28
Assíntota Horizontal ..................................................................................................................................30
O Limite Fundamental ...................................................................................................................................31
Continuidade ....................................................................................................................................................34
Introdução
O conceito de limite de uma função f é um dos mais importantes do Cálculo Diferencial e Integral.
No século XVIII, o conceito de limite foi abordado intuitivamente, ou seja, verificando que o valor de f em
x, f ( x ) , tende para um determinado número L, quando x tende para um número a. Isso é equivalente a
afirmar que quanto mais próximo de L estiver o valor f ( x ) , mais próximo de a estará x. A grande questão
envolvida nesta definição é o significado da palavra “próximo”, pois dependendo da situação o que é
próximo para alguns pode não ser para outros. Vejamos: na Física é comum os astrônomos medirem a
proximidade em anos-luz; na Biologia, em determinadas situações, a proximidade se estabelece apenas
quando o resultado de uma mensuração está próximo do valor exato L, ou seja, se estiver a 10 −6 cm de L.
Assim, para evitar ambigüidades, é preciso formular uma definição de limite, com o rigor que a matemática
exige, e sem utilizar a palavra “próximo”. Conforme veremos, isso é garantido empregando na definição,
epsilon ( ε ) e delta ( δ ), introduzida por Cauchy e Weierstrass, pois esta é precisa e aplicável a qualquer
situação.
A importância do estudo de limites é que podemos passar da taxa média de variação ao conceito
mais útil de taxa instantânea de variação.
Limites
Imaginemos um objeto pontual movimentando-se sobre uma reta orientada, sujeito a uma lei de
movimento s = s ( t ) que fornece a posição s do objeto a cada instante de tempo t.
Consideremos que s seja medido em centímetros, que t seja medido em segundos e que o início do
experimento seja feito no instante t = 0 . Algumas perguntas pertinentes ao movimento do objeto podem ser
feitas: Como obter a velocidade do objeto num dado instante de tempo? Qual é o significado da velocidade
do objeto num instante de tempo?
Vamos particularizar nosso problema para obtermos algumas respostas.
Considere um objeto que se movimenta segundo a lei s ( t ) = 3 + 6t − 5t 2 + t 3 . No instante inicial
t = 0 o objeto encontra-se na posição s (0) = 3 ; no instante t = 2 , o objeto encontra-se na posição
s (2) = 3 + 6 ⋅ 2 − 5 ⋅ 2 2 + 2 3 = 3 . Então, após 2 segundos do início do movimento o objeto volta a ocupar a
posição inicial. Pergunta-se: Qual é a velocidade do objeto precisamente no instante t = 2 ? Qual é o
significado da velocidade instantânea?
No ensino médio conseguíamos calcular a velocidade média de um objeto entre dois instantes de
tempo quando conhecíamos sua lei de movimento e trabalhávamos com a equação v = v 0 + at , da velocidade
de um objeto sujeito a um movimento retilíneo uniformemente acelerado, onde v 0 é a velocidade inicial do
objeto e a sua aceleração. Mas não éramos alertados que a velocidade da equação não era uma velocidade
média, mas sim uma velocidade instantânea.
Tentaremos responder as questões levantadas acima através de aproximações.
Para isso, vamos considerar o intervalo de tempo [1, 3]. Nos instantes t = 1 e t = 3 o objeto está,
respectivamente, nas posições s (1) = 5 e s (3) = 3 .
s(2)
s(1)
3
5
s(0)
0
A velocidade média neste intervalo de tempo é dada por v m =
s (3) − s (1)
.
3−1
Para t ∈ [ 1, 3 ] a velocidade média é de −1 cm/s. Como o instante t = 2 pertence ao intervalo [1, 3],
podemos, inicialmente, tomar a velocidade no instante t = 2 como sendo v (2) = −1 cm/s.
Por outro lado, a expressão v = v 0 + a t nos fornece, no intervalo entre t = 1 e t = 3, uma
velocidade não constante, pois a ≠ 0 . Assim, pode ocorrer que no instante t = 2 a velocidade instantânea
esteja longe do valor v (2) = −1 cm/s. Se considerarmos um intervalo de tempo de menor amplitude que [1,
3], mas que contenha t = 2, poderemos aproximar melhor a velocidade no instante t = 2.
Vamos considerar o intervalo [1,2 ; 2,8]. Neste caso, a velocidade média será:
vm =
s (2, 8) − s (1, 2)
= −1, 36 cm/s.
2, 8 − 1, 2
Como a velocidade média no intervalo de tempo [1,2 ; 2,8] é igual a −1,36 cm/s é compreensível
que a velocidade no instante t = 2 esteja mais próxima desse valor que de −1 cm/s.
Para melhorar nossa aproximação, tomemos o intervalo [1,4 ; 2,6]. Neste caso, a velocidade média
será:
vm =
s (2, 6) − s (1, 4)
= −1, 64 cm/s.
2, 6 − 1, 4
Podemos continuar considerando intervalos da forma [2 − δ , 2 + δ ] com o valor de δ assumindo
números positivos cada vez menores, como, por exemplo: δ = 0, 4 ; δ = 0, 2 ; δ = 0,1 ; δ = 0,05 etc.
Procedendo dessa maneira definimos uma função f (δ ) que calcula a velocidade média no
intervalo [2 − δ , 2 + δ ] , dada por
f (δ ) =
s (2 + δ ) − s (2 − δ )
.
2δ
Observe que os três valores da velocidade média calculados anteriormente são os valores de f
quando δ assume os valores 1; 0,8 e 0,6, respectivamente.
Intuitivamente, percebemos que quanto menor o valor de δ , mais a velocidade média no intervalo
[2 − δ , 2 + δ ] estará se aproximando do valor da velocidade instantânea em t = 2 .
Utilizando uma calculadora científica podemos verificar os cálculos mostrados na seguinte tabela:
δ (s)
Velocidade média (cm/s)
1
-1
0,1
-1,99
0,01
-1,9999
0,001
-1,999999
0,0001
-2,00000000
A partir do valor δ = 0,0001 a calculadora científica de dez dígitos começa a arredondar os
cálculos, indicando como resultado o valor f (δ ) = −2 .
Na verdade, de modo intuitivo, calculamos o limite da velocidade média do objeto em intervalos do
tipo [2 − δ , 2 + δ ] , quando δ se aproxima de zero por valores maiores que zero. Ou equivalentemente,
calculamos o limite da função f (δ ) quando δ tende a zero pela direita.
s (2 + δ ) − s (2 − δ )
, observamos
2δ
que a função não está definida para δ = 0 . Assim, não podemos substituir o valor "δ = 0" na expressão da
função.
Ao prestarmos atenção à expressão que define a função f , f (δ ) =
Esse tipo de situação ocorre com freqüência no Cálculo. Por exemplo, ao procurar o domínio de
uma função verificamos que a mesma não está definida num determinado ponto. Em razão disso, podemos
perguntar: o que ocorre com os valores da função para pontos próximos do ponto onde a função não está
definida?
x 2 + 3x − 4
. Como Dom f = − {1} ,
x −1
não podemos calcular o valor da função no ponto x = 1 . Porém, podemos estudar o comportamento da
função nas proximidades deste ponto. A tabela a seguir apresenta alguns valores de f ( x ) para valores de x
próximos de 1.
Exemplo 1: Consideremos a função f definida por f ( x ) =
f(x)
x
f(x)
x
0,9
4,9
1,1
5,1
0,99
4,99
1,01
5,01
0,999
4,999
1,001
5,001
0,9999
4,9999
1,0001
5,0001
0,99999
4,99999
1,00001
5,00001
0,999999
4,999999
1,000001
5,000001
0,9999999
4,9999999
1,0000001
5,0000001
0,99999999
4,99999999
1,00000001
5,00000001
0,999999999
4,999999999
1,000000001
5,000000001
O que ocorre com f ( x ) quando x se aproxima de 1 por valores maiores que 1? E por valores
menores que 1? Diante das respostas a tais questões, percebemos que o valor da função f está próximo de 5,
quando x está bem próximo de 1.
Quando isto ocorre dizemos que existe o limite de f ( x ) quando x tende a 1 e é igual a 5. Neste
caso, escrevemos lim f ( x ) = 5.
x →1
Exercício 1: Considere agora uma função f cujo gráfico é dado por
y
5
2
0
3
x
O que ocorre com f(x) quando x se aproxima de 3 por valores maiores que 3? E quando se
aproxima de 3 por valores menores que 3? Neste caso, o que ocorre com os valores de f(x) quando x está
bem próximo de 3?
Esse processo de aproximar a variável independente de um número c e observar o comportamento
da variável dependente, verificando se esta tende a um número real L, chama-se cálculo de limites. Com isso,
no primeiro exemplo, dizemos que os limites laterais à direita e à esquerda existem e são iguais e, portanto,
existe o limite de f(x) quando x tende para 1. No exemplo 1, tais limites laterais são diferentes e, portanto,
dizemos que não existe o limite de f(x) quando x tende a 3.
O cálculo de limites é um processo imprescindível no desenvolvimento do Cálculo. A princípio,
ainda no século XVII, ele era compreendido e utilizado sem uma definição matemática formal. Newton e
Leibniz faziam uso de cálculos de limites e suas propriedades para definir “derivadas” e “integrais”, mas
nunca utilizaram a definição que aqui apresentamos, pois essa definição formal só foi aprimorada em meados
do século XIX com a influência de matemáticos que iniciaram o uso do “rigor” na Análise. Dentre esses
matemáticos, citamos com destaque Augustin Cauchy (1789–1857) e Karl Weierstrass (1815–1897).
Definição de Limite
Definição: Sejam f uma função definida num intervalo aberto ( a , b ) , exceto possivelmente em
x = c , c ∈ ( a , b ) , e L ∈ . Dizemos que o limite lateral à direita de f ( x ) no ponto c é igual a L , cuja
notação é lim f ( x ) = L , se dado ε > 0 existe δ > 0 tal que f ( x ) − L < ε sempre que 0 < x − c < δ .
x →c +
Para ilustrar essa definição, tomemos a função g : − {4} → tal que g ( x ) = 2x + 1 . A função
não está definida no ponto x = 4 mas isso não nos impede de pesquisarmos o comportamento de g quando
x se aproxima de 4 pela direita. Mediante o uso de substituições, verificamos que quanto mais próximo de 4
estiver a variável x, mais próximo de 9 estará o valor g ( x ) . Isso nos sugere que o limite de g ( x ) = 2x + 1
quando x tende a 4 pela direita é 9. Esse valor 9 é expresso na definição com a letra L. Então, dada uma
quantidade positiva ε devemos ser capazes de exibir uma outra quantidade positiva δ tal que se tomarmos
um número x ∈ (4, 4 + δ ) , então o valor g ( x ) ∈ (9,9 + ε ) ⊂ (9 − ε ,9 + ε ) .
y
9+ε
9
9-ε
0
4-δ
4 4+δ
x
Se a quantidade positiva ε for igual a 1, deveremos ser capazes de exibir δ tal que para todo
x ∈ (4, 4 + δ ) seja verdadeiro que g ( x ) ∈ (8,10) . Se construirmos e observarmos o gráfico de g podemos
1
1
exibir δ = . Assim, para todo x ∈ (4, 4 + ) concordamos que g ( x ) ∈ (8, 10) .
2
2
1
, deveremos ser capazes de exibir δ tal que para todo
2
1
x ∈ (4, 4 + δ ) seja verdadeiro que g ( x ) ∈ (8,5 , 9,5) . Podemos exibir δ = , ou mesmo um δ menor que
4
1
este, tal que para todo x ∈ (4, 4 + ) tem-se g ( x ) ∈ (8,5, 9,5) .
4
Se a quantidade positiva ε for igual a
Percebemos que para qualquer quantidade positiva ε , por menor que ela seja, conseguiremos
1
exibir uma quantidade positiva δ , por exemplo δ = ε , tal que se x ∈ (4, 4 + δ ) , então
2
g ( x ) ∈ (9 − ε , 9 + ε ) .
y
9+ε
g(x)
9
4 x 4+δ
0
x
Mas o raciocínio anterior não é uma demonstração formal de que lim+ (2 x + 1) = 9 . Para realizar
x →4
essa demonstração observemos que
g ( x ) − 9 = 2x + 1 − 9 = 2x − 8 = 2( x − 4) = 2 x − 4 .
Logo, dado ε > 0 , se tomarmos δ =
ε
ε
ε
2
teremos
ε
x ∈ (4,4 + ) ⇒ 0 < x − 4 < ⇒ 2 x − 4 < 2 ⇒ 2( x − 4) < ε ⇒ 2x + 1 − 9 < ε ⇒ g ( x ) − 9 < ε .
2
2
2
Essa relação dinâmica entre uma quantidade positiva e tão pequena quanto se queira ε e a
quantidade exibida δ é que é o âmago da definição de limite e está escrita na forma:
“Dado ε > 0 existe δ > 0 tal que f ( x ) − L < ε sempre que 0 < x − c < δ ”.
Percebemos que qualquer outro valor menor que
a demonstração de que lim (2 x + 1) = 9 , se exibirmos δ =
x →4
+
Dado ε > 0 se tomarmos δ =
x ∈ (4, 4 +
ε
15
⇒ 2( x − 4) <
ε
15
ε
2
ε
15
pode ser exibido como δ . Vejamos como fica
.
teremos
)⇒ 0 < x − 4 <
ε
15
⇒2 x −4 <2
ε
15
⇒
2
ε < ε ⇒ 2x + 1 − 9 < ε ⇒ g ( x ) − 9 < ε .
15
De maneira análoga definimos o limite lateral à esquerda.
Definição: Sejam f uma função definida num intervalo aberto ( a , b ) , exceto possivelmente em
x = c , c ∈ ( a , b ) , e L ∈ . Dizemos que o limite lateral à esquerda de f ( x ) no ponto c é igual a L , cuja
notação é lim f ( x ) = L , se dado ε > 0 existe δ > 0 tal que f ( x ) − L < ε , sempre que −δ < x − c < 0 .
x →c −
A definição anterior significa que os valores da função f se aproximam de L quando x tende a c
por valores menores que c.
Exemplo 2: Sejam f ( x ) = 3x − 2 e o ponto c = 2 . Vamos mostrar que lim f ( x ) = 4 . Para isso, é
x → 2−
necessário que, para um dado ε > 0 arbitrário, encontremos um valor δ > 0 tal que ocorra ( 3x − 2 ) − 4 < ε
sempre que −δ < x − 2 < 0 . Mas
( 3x − 2 ) − 4 = 3 x − 6 = 3 ( x − 2 ) = 3 x − 2 .
Por outro lado, −δ < x − 2 < 0 ⇒ 0 < x − 2 < δ . Assim, temos 3 x − 2 < 3δ e, portanto, tomando
δ=
ε
3
, temos ( 3x − 2 ) − 4 < ε sempre que −
ε
3
< x −2 <0.
y
y = 3x − 2
4+ε
4
f (x)
4-ε
0
2-δ x 2 2+δ
x
Exercício 2: Demonstre, usando a definição, que lim+ (3x − 2) = 4 .
x →2
Agora estamos em condição de definir o limite de uma função f .
Definição: Sejam f uma função definida num intervalo aberto ( a , b ) , exceto possivelmente em
x = c , c ∈ ( a , b ) , e L ∈ . Dizemos que o limite de f ( x ) no ponto x = c é igual a L se existem os limites
laterais à direita e à esquerda de c e, além disso, são iguais. Equivalentemente, temos:
dado ε > 0 existe δ > 0 tal que f ( x ) − L < ε , sempre que 0 < x − c < δ .
Notação: lim f ( x ) = L .
x →c
É importante observar que:
•
O limite de uma função f no ponto c não diz nada sobre f ( c ) ; mais do que isso, a função
f não precisa sequer estar definida em x = c , ou seja, o ponto c não precisa pertencer ao
domínio da função f .
•
A condição 0 < x − c < δ indica que x ≠ c ;
•
Se lim f ( x ) ou lim f ( x ) não existirem, então não existe lim f ( x ) . Porém, esta não é
x →c +
x →c −
x →c
a única situação em que o limite da função não existe em x = c, pois a existência do limite
pode depender da forma com que x se aproxima de c. Isso ocorre, por exemplo, com a
função de Dirichelet apresentada no exemplo a seguir.
Exemplo 3: Considerando a função f ( x ) = 3x − 2 e o ponto c = 2 do exemplo 2, podemos
concluir que lim f ( x ) = 4 .
x →2
Exemplo 4: Dada f ( x ) =
x 2 + 3x − 4
, vamos calcular lim f ( x ) .
x →1
x −1
Para essa função temos Dom f = − {1} . Ao tentarmos uma simples substituição de x por 1 no
polinômio do numerador obtemos o valor 0, o que significa que o número 1 é uma raiz desse polinômio.
Assim, x 2 + 3x − 4 = ( x − 1)( x + 4) .
Portanto, como no cálculo do limite a variável x assume valores diferentes de 1, temos que
( x − 1)( x + 4)
lim f ( x ) = lim
= lim( x + 4) = 5 .
x →1
x →1
x →1
x −1
 1, x ∈
Exemplo 5: A função de Dirichelet definida por f ( x ) = 
−1, x ∉
algum de seu domínio.
não possui limite em ponto
Para demonstrar que este limite não existe, vamos nos aproximar do ponto x = c de duas formas
diferentes: quando x → c por valores racionais e quando x → c por valores irracionais. Vejamos:
Se c ∈
, como
é denso em
, podemos escolher valores de x racionais que se aproximam de
c. Logo,
lim f ( x ) = lim 1 = 1
x →c
x →c
(I)
Por outro lado, como o conjunto dos números irracionais também é denso em
x irracionais que se aproximam de c, obtemos
lim f ( x ) = lim ( −1) = − 1
x →c
De (I) e (II) segue que lim f ( x ) não existe.
x →c
x →c
(II)
, se escolhermos
Exercício 3: Calcule, se possível, os limites: lim k( x ) , lim k( x ) , lim k( x ) , lim k( x ) , lim k( x )
x →−4
e
x →1
x →5
x →8
x →0
lim k( x ) , considerando a função k( x ) cujo gráfico está esboçado na figura a seguir. Se não for possível
x → 32
calcular os limites, justifique-os.
y
5
4
3
2
-4
-2
1
0
5
8
x
-4
−1,
x < −1

Exercício 4: Considere a função h( x ) = x ,
−1 ≤ x ≤ 2 .
 2
−x + 5, x > 2
Calcule, se possível, os limites lim h( x ) ,
x →−1
lim h( x ) , lim h( x ) ,
x →2
x →0
lim h( x ) e lim h( x ) . Caso
x →−100
x →10
contrário, justifique.
A definição de limite utilizando ε e δ é de grande importância teórica e torna precisa a noção de
“estar próximo”. O seguinte resultado estabelece que quando o limite existe, ele é único.
Teorema (unicidade do limite): Seja f uma função definida num intervalo aberto ( a , b ) , exceto
possivelmente em x = c , c ∈ ( a , b ) . Se lim f ( x ) = L1 e lim f ( x ) = L 2 , então L1 = L 2 .
x →c
x →c
Demonstração: Suponhamos, por absurdo, que L1 ≠ L 2 . Seja ε =
existem δ1 > 0 e δ 2 > 0 , tais que
0 < x − c < δ1 ⇒ f ( x ) − L1 < ε
| L1 − L 2 |
. Por definição,
2
e 0 < x − c < δ2 ⇒ f ( x ) − L2 < ε .
Tomando δ = min {δ 1 , δ 2 } tem-se, para 0 < x − c < δ , que
L1 − L 2 = L1 − f ( x ) + f ( x ) − L 2 ≤ L1 − f ( x ) + f ( x ) − L 2 < ε + ε = L1 − L 2 .
Mas isto é absurdo, logo L1 = L 2 .
‘
Exemplo 6: Seja f ( x ) = k uma função constante. Vamos mostrar que, para qualquer número c,
temos lim f ( x ) = k .
x →c
De fato, dado ε > 0 podemos exibir δ > 0 assumindo qualquer valor, por exemplo, δ = 11 .
Se 0 < x − c < δ = 11 , então f ( x ) − k = k − k = 0 < ε .
Perceba que, como f ( x ) − k < ε independe do particular valor numérico de δ , podemos tomar
qualquer δ > 0 que teremos a desigualdade desejada. Dessa forma, lim f ( x ) = k , para todo c ∈
tivermos, por exemplo, f ( x ) = −3π , então lim f ( x ) = −3π .
x →c
. Assim, se
x →2
Exemplo 7: Se m e b são constantes, com m ≠ 0 e f ( x ) = mx + b , vamos mostrar que
lim f ( x ) = m .c + b , para qualquer número c.
x →c
Pela definição, dado ε > 0 devemos exibir
δ > 0 , tal que f ( x ) − ( mc + b ) < ε sempre que
0< x −c <δ .
f ( x ) − ( mc + b ) = mx + b − ( mc + b ) = mx + b − mc − b = m ( x − c ) = m x − c , tomando
Como
δ=
ε
|m|
, obtemos que
0< x −c <
ε
m
⇒ m x −c < m
ε
m
⇒ m( x − c ) < ε ⇒ mx + b − mc − b < ε ⇒ f ( x ) − ( mc + b ) < ε .
Exercícios
5. Mostre que, no exemplo 7, podemos tomar o valor δ =
ε
3m
para demonstrar que
lim f ( x ) = mc + b .
x →c
6. Demonstre que se f ( x ) = 7x + 8 , então lim f ( x ) = −6.
x →−2
Propriedades dos Limites
A partir dessa seção, sempre que possível, não utilizaremos a definição para obter limite de funções.
Vamos, assim, apresentar e demonstrar algumas propriedades que nos permitirão tornar o cálculo de limites
um procedimento mais simples.
Proposição: Sejam f e g duas funções definidas em um intervalo ( a , b ) exceto possivelmente
em c ∈ ( a , b ) . Se lim f ( x ) = L1 e lim g ( x ) = L 2 , então:
x →c
x →c
a) lim[ f ( x ) + g ( x )] = L1 + L 2 ;
x →c
b) lim[ k ⋅ f ( x )] = k ⋅ L1 , ∀k ∈ ;
x →c
c) lim[ f ( x ) ⋅ g ( x )] = L1 ⋅ L 2 ;
x →c
d) lim
x →c
f ( x ) L1
, desde que L 2 ≠ 0 ;
=
g( x ) L2
e) lim n f ( x ) = n L1 , se n é um número natural ímpar;
x →c
f) lim n f ( x ) = n L1 , se n é número natural par não-nulo e L1 ≥ 0 .
x →c
Demonstração: As demonstrações dos itens e e f serão feitas após as demonstrações de alguns
resultados de continuidade de função.
a) Por hipótese, dado ε > 0 existem δ1 > 0 e δ 2 > 0 tais que
0 < x − c < δ 1 ⇒ f ( x ) − L1 <
ε
0 < x − c < δ2 ⇒ g( x ) − L2 <
e
2
ε
2
.
Então, tomando δ = min{δ1 , δ 2 } , temos que
0 < x − c < δ ⇒ ( f ( x ) + g ( x )) − ( L1 + L 2 ) ≤ f ( x ) − L1 + g ( x ) − L 2 <
ε
2
+
ε
2
= ε.
Assim, lim[ f ( x ) + g ( x )] = L1 + L 2 .
x →c
b)
(i) Se k = 0 , então k ⋅ f ( x ) = 0 ;
(ii) Se k ≠ 0 , por hipótese, dado ε > 0 existe δ > 0 tal que
0 < x − c < δ ⇒ f ( x ) − L1 <
ε
.
k
Então, utilizando esse valor de δ obtemos as implicações
0 < x − c < δ ⇒ f ( x ) − L1 <
ε
k
⇒ k f ( x ) − L1 < k
Assim, lim[ k ⋅ f ( x )] = k ⋅ L1 , ∀k ∈
x →c
ε
k
⇒ k ⋅ f ( x ) − k ⋅ L1 < ε .
.
c)
(i) Demonstremos primeiramente o caso particular, onde lim f ( x ) = L1 e lim h( x ) = 0 implicam
que lim[ f ( x ) ⋅ h( x )] = 0 .
x →c
x →c
x →c
Por hipótese, dado ε = 1 existe δ1 > 0 tal que 0 < x − c < δ1 ⇒ f ( x ) − L1 < 1 . Disso deduzimos
que f ( x ) = f ( x ) − L1 + L1 ≤ f ( x ) − L1 + L1 < 1 + L1 , sempre que 0 < x − c < δ1 .
Então, podemos escrever que 0 < x − c < δ1 ⇒ f ( x )h( x ) = f ( x ) h( x ) < (1 + L1 ) h( x ) .
Como
estamos
admitindo
0 < x − c < δ 2 ⇒ h( x ) − 0 <
ε
1 + L1
que
lim h( x ) = 0 ,
x →c
dado
ε >0
existe
δ2 > 0
tal
que
.
Tomando δ = min{δ1 , δ 2 } segue que
0 < x − c < δ ⇒ f ( x )h ( x ) − L1 ⋅ 0 = f ( x )h ( x ) < (1 + L1 )
ε
1 + L1
= ε . Ou seja, lim[ f ( x ) ⋅ h( x )] = 0 .
x →c
(ii) Usando o item a, temos lim[ g ( x ) − L 2 ] = 0 e, pelo resultado provado, para h( x ) = g ( x ) − L 2 ,
x →c
temos lim f ( x )[ g ( x ) − L 2 ] = 0 .
x →c
Usando os itens a e b, temos lim L 2 [ f ( x ) − L1 ] = 0 . E, finalmente, podemos escrever
x →c
lim[ f ( x ) g ( x )] = lim[ f ( x ) ( g ( x ) − L 2 ) + L 2 ( f ( x ) − L1 ) + L1 L 2 ] =
x →c
x →c
= lim f ( x )[ g ( x ) − L 2 ] + lim[ L 2 ( f ( x ) − L1 ) ] + lim[ L1 L 2 ] = 0 + 0 + L1 L 2 .
x →c
x →c
x →c
Assim, lim[ f ( x ) ⋅ g ( x )] = L1 ⋅ L 2 .
x →c
d) Basta provar que lim
1
1
.
=
g( x ) L2
Por hipótese, dado ε =
L2
L
existe δ1 > 0 tal que 0 < x − c < δ1 ⇒ g ( x ) − L 2 < 2 .
2
2
x →c
Dessa maneira, 0 < x − c < δ1 ⇒ L 2 = L 2 − g ( x ) + g ( x ) ≤ L 2 − g ( x ) + g ( x ) <
Então, 0 < x − c < δ1 ⇒ L 2 −
L2
+ g( x ) .
2
L2
L
1
2
< g( x ) ⇒ 2 < g( x ) ⇒
<
.
2
2
g( x ) L2
Conseqüentemente,
0 < x − c < δ1 ⇒
L − g( x )
1
1
1
2
−
= 2
=
g ( x ) − L 2 < 2 g ( x ) − L 2 , onde
g( x ) L2
g ( x )L 2
L2 g(x )
M
0 < M < L2 .
Novamente, por hipótese, dado ε > 0 existe δ 2 > 0 tal que 0 < x − c < δ 2 ⇒ g ( x ) − L 2 <
Tomando δ = min{δ 1 , δ 2 } teremos
0< x −c <δ ⇒
1
1
2
2 M2
−
< 2 g( x ) − L2 < 2
ε = ε.
g( x ) L2 M
M 2
M2
ε.
2
Portanto, lim
x →c
1
1
.
=
g( x ) L2
Podemos calcular os limites mais rapidamente, utilizando apenas as propriedades anteriores.
Exemplo 8: Seja h( x ) = x 2 + 2 x + 1 . Então, utilizando as propriedades temos que lim h ( x ) = 16 ,
x →3
pois
(
lim( x 2 + 2 x + 1) = lim x
x →3
x →3
)
2
+ 2 lim x + lim 1 = 9 + 6 + 1 = 16 .
x →3
x →3
x 3 + 2x + 1
4
. Então, lim h( x ) = = 2 . Mas lim h( x ) não pode ser
x →1
x →−1
x +1
2
calculado mediante o uso das propriedades porque o limite do denominador da expressão de h( x ), quando
x tende a –1, é zero.
Exemplo 9: Seja h( x ) =
(
)
1
Exemplo 10: Seja g ( x ) = 4 x 3 + 2x + 2 3 . Então, lim g ( x ) = 2 , pois
(
x →1
( ) + 2 lim x + 2 =
)
lim g ( x ) = 3 lim 4 x 3 + 2 x + 2 = 3 4 lim x
x →1
x →1
3
x →1
x →1
3
4+2+2 = 38 =2.
Como conseqüência da proposição anterior obtemos os seguintes resultados:
Corolário:
n
n
i =1
i =1
n
n
i =1
i =1
a) lim ∑ f i ( x ) = ∑ lim f i ( x ) , se lim f i ( x ) existe, para cada 1 ≤ i ≤ n ;
x →c
x →c
x →c
b) lim ∏ f i ( x ) = ∏ lim f i ( x ) , se lim f i ( x ) existe, para cada 1 ≤ i ≤ n ;
x →c
x →c
x →c
c) Se f é uma função polinomial, então lim f ( x ) = f ( c ) ;
x →c
d) Se f é uma função racional da forma f ( x ) =
p( x )
p( c )
com q( c ) ≠ 0 , então lim f ( x ) =
.
x →c
q( x )
q( c )
Exemplo 11: Seja h( x ) = 5x 3 + 2x 2 − 3x + 1 . Pelo item c do corolário anterior temos
lim h( x ) = −25 .
x →−2
Exemplo 12: Seja h( x ) =
x 2 − 2x + 1
. Pelo item d do corolário anterior temos lim h( x ) = 0 .
x →1
x +1
Proposição: Sejam f e g funções definidas num intervalo aberto ( a , b ) , tais que f ( x ) = g ( x ) ,
exceto possivelmente em x = c , c ∈ ( a , b ) . Se lim g ( x ) = L , então lim f ( x ) = L .
x →c
x →c
Demonstração: Dado ε > 0 , existe δ > 0 tal que 0 < x − c < δ ⇒ g ( x ) − L < ε . Mas, por
hipótese, f ( x ) = g ( x ) , para x ≠ c . Logo, tomando o mesmo δ anterior podemos escrever
0 < x − c < δ ⇒ f ( x ) − L = g ( x ) − L < ε , ou seja, lim f ( x ) = L .
x →c
Exemplo 13: O item d do corolário anterior não é válido quando q( c ) = 0 . Apesar disso, se
p( c ) = 0 podemos estudar o comportamento de f quando x tende a c . De fato, quando q( c ) = 0 temos
q( x ) divisível por
( x − c ) , ou seja, q( x ) = ( x − c )m .h( x ) onde h( c ) ≠ 0 e m ∈
p( x ) = ( x − c ) .k( x ) onde k( c ) ≠ 0 e n ∈
n
∗
∗
. Temos também
. Temos três casos a considerar:
1. n = m : neste caso, temos lim f ( x ) =
x →c
( x − c )n k( x ) k( x )
k( c )
, pois f ( x ) =
=
, x ≠ c e h( c ) ≠ 0 .
h( c )
( x − c )m h ( x ) h ( x )
2. n > m : neste caso, temos lim f ( x ) = 0 , pois f ( x ) =
x →c
( x − c )n k( x )
k( x )
= ( x − c )n − m
, x ≠c.
m
h( x )
( x − c ) h( x )
3. n < m : neste caso o limite não existe e será estudado mais adiante com detalhes.
O próximo teorema necessita de um conceito muito importante, que pertence a um ramo da
matemática chamado Topologia, a saber, o conceito de vizinhança de um ponto c. Chamamos de vizinhança
de um ponto c, qualquer intervalo aberto contendo esse ponto.
Teorema: Toda função que possui limite num ponto c é limitada numa vizinhança do ponto c.
Este teorema é bem intuitivo, pois quando x se aproxima do ponto c , f ( x ) se aproxima de um
número L. Então, deve existir uma vizinhança V do ponto c , tal que f ( x ) ≤ k , para todo x ∈V e para
algum valor real positivo k .
Demonstração: Por hipótese, tomemos lim f ( x ) = L . Assim, dado ε > 0 existe δ > 0 tal que,
x →c
para pontos x ≠ c no intervalo ( c − δ , c + δ ) , a distância entre o valor f ( x ) e o número L fica menor que
ε , isto é, f ( x ) − L < ε . Devemos mostrar que existe um intervalo ( c − λ , c + λ ) tal que x ∈ ( c − λ , c + λ )
implica
em
f (x ) ≤ k ,
para
algum
valor
real
positivo
k.
Ora,
tomando
λ =δ
teremos
0 < x − c < λ ⇒ f ( x ) = ( f ( x ) − L ) + L ≤ f ( x ) − L + L < ε + L . Como o valor f ( c ) , caso exista, pode
ser diferente de L, tomemos k = max { L + ε ,
f (c )
} . Assim, para x ∈ ( c − λ , c + λ ) temos
x − 4,
x <5

Exemplo 14: Dada a função f ( x ) = −π ,
x =5 ,
 2
x − 10x + 26, x > 5
lim f ( x ) = lim ( x − 4) = 1
x →5 −
x →5 −
e
vamos calcular lim f ( x ) .
lim f ( x ) = lim ( x 2 − 10 x + 26) = 1 .
x →5+
x →5+
f (x ) ≤ k .
x →5
Como lim f ( x ) = lim f ( x ) = 1 , temos que lim f ( x ) = 1 .
x →5−
x →5 +
x →5
A função f é limitada em intervalos abertos que contêm x = 5 . Seguindo o raciocínio da
demonstração do teorema anterior, dado, por exemplo, ε = 0,5 existe δ > 0 tal que se x ≠ 5 e
x ∈ (5 − δ ,5 + δ ) , então f ( x ) − 1 < 0,5 . Então, tomando k = max{ (1 + 0,5 ) ; −π } = π podemos escrever:
se x ∈ (5 − δ , 5 + δ ) , então
f (x ) < π .
Veja pelo esboço do gráfico de f mostrado a seguir, que esta função é limitada em intervalos que
contêm o ponto x = 5 .
y
1
0
5
x
-π
-4
Exemplo 15: A afirmação “Se uma função f é limitada numa vizinhança do ponto c , então existe
lim f ( x ) ” é falsa.
x →c
2, x < 0
. Esta é uma função limitada em toda a reta
Considere a função f ( x ) = 
, pois
1, x ≥ 0
f ( x ) ≤ 2, ∀x ∈ . Mas lim f ( x ) = lim 2 = 2 e lim f ( x ) = lim 1 = 1 e, portanto, não existe lim f ( x ) .
x →0 −
x →0 −
x →0 +
x →0 +
x →0
Um outro resultado importante é dado a seguir.
Teorema (Confronto ou Sanduíche): Sejam f , g e h funções definidas num intervalo aberto
( a , b ) , exceto possivelmente em x = c , c ∈ ( a , b ) . Suponha que f ( x ) ≤ g ( x ) ≤ h ( x ), ∀x ∈ ( a , b ) , exceto
possivelmente em x = c . Se lim f ( x ) = lim h( x ) = L , então lim g ( x ) = L .
x →c
Demonstração:
Como
x →c
x →c
lim f ( x ) = lim h( x ) = L , dado ε > 0 existe δ > 0 , tal que se
x →c
x →c
0 < x − c < δ , então
| f (x ) − L|< ε
e |h ( x ) − L | < ε .
Segue que
L − ε < f (x ) < ε + L
e
L − ε < h( x ) < ε + L .
Portanto, para x ∈( a , b ) tal que 0 < | x − c | < δ , tem-se
L − ε < f ( x ) ≤ g ( x ) ≤ h( x ) < ε + L .
Desta forma, | g ( x ) − L |< ε , para x ∈( a , b ) sempre que 0 < | x − c | < δ , ou seja, lim g ( x ) = L .
x →c
Corolário: Sejam f e g uma funções definidas num intervalo aberto ( a , b ) , exceto possivelmente
em x = c , c ∈ ( a , b ) . Se lim f ( x ) = 0 e g é limitada, então lim [ f ( x ) ⋅ g ( x )] = 0 .
x →c
x →c
O teorema do confronto também vale para limites laterais e sua demonstração será deixada como
exercício.
Exemplo 16: Sabendo que 1 −
x sen x
x2
<
< 1 , para todos os valores de x próximos de
6
2 − 2 cos x
zero, segue do teorema do confronto que lim
x →0
 x2 
x sen( x )
= 1 , pois lim  1 −
 = 1 e lim 1 = 1 .
x →0
x →0
2 − 2 cos ( x )
6 

Exercícios
7. Calcule lim
5
x →3
x 3 − 3x 2 + 3x − 9
, indicando as propriedades utilizadas.
x2 −9
8. Calcule os seguintes limites:
a) lim 52
b) lim( −8)
d) lim (4 + x )
e) lim
x →−2
x →0
+
x3 − 1
x →1 x − 1
c) lim
x →8
+
x →3
x 3 − 27
x2 +1
f) lim
h →0
x +h − x
, x >0
h
9. Para cada função f definida a seguir calcule lim− f ( x ) e lim+ f ( x ) e esboce o gráfico de f .
x →2
 3x , x ≤ 2
a) f ( x ) =  2
x , x > 2
x →2
 3x + 5, x ≤ 2
b) f ( x ) = 
.
4 − 2 x , x > 2
3x + 5, x ≠ 2
10. Dada f ( x ) = 
, encontre lim f ( x ) , mostre que lim f ( x ) ≠ f (2) e trace um
x →2
x →2
x >2
 4,
esboço do gráfico de f.
11. Nos itens a seguir, encontre os limites indicados, se existirem. Caso não existam, justifique.
Esboce o gráfico de cada função.
 2, x < 1

a) f ( x ) = −1, x = 1 .
−3, x > 1

lim f ( x ) ; lim f ( x ) ; lim f ( x ) ; lim f ( x ) ; lim f ( x ) e lim f ( x ) .
x →1+
x →1−
x →1
x →0
x →−3
x →2
3 + t 2 , t < −2

b) f ( x ) = 0,
t =2 .
11 − t 2 , t > −2

lim f ( x ) ; lim f ( x ) ; lim f ( x ) ; lim f ( x ) ; lim f ( x ) e lim f ( x )
x →−2 +
x →−2 −
c) f ( t ) =
x →−2
x →0
x →−1
x →−4
|t |
.
t
lim f ( t ) ; lim f ( t ) e lim f ( t ) .
t →0 +
t →0 −
t →0
Limites Infinitos
Considere as funções definidas por f ( x ) =
1
−1
e g( x ) =
. Seus respectivos gráficos estão
x
x −3
esboçados a seguir.
y
y
x
0
x
Graf g
Graf f
ponto x = 0 e do
Façamos um estudo do comportamento de f nas proximidades do
comportamento de g nas proximidades do ponto x = 3 , mediante alguns cálculos.
x
x
f (x )
x
f (x )
x
g( x )
g( x )
-0,1
10
0,1
10
2,9
–10
3,1
–10
-0,01
100
0,01
100
2,99
–100
3,01
–100
-0,001
1000
0,001
1000
2,999
–1000
3,001
–1000
-0,0001
10000
0,0001
10000
2,9999
–10000
3,0001
–10000
-0,00001
100000
-0,000001 1000000
0,00001
100000
2,99999
–100000
3,00001
–100000
0,000001
1000000
2,999999
–1000000
3,000001
–1000000
Observamos, pelo quadro anterior, que quando x se aproxima de 0 pela esquerda ( x → 0 − ) os
valores da função f se tornam arbitrariamente grandes ( f ( x ) → +∞ ) .
Analogamente, quando x se aproxima de 0 pela direita ( x → 0 + ) os valores da função f também se
tornam arbitrariamente grandes ( f ( x ) → +∞ ) . Neste caso, dizemos que o limite de f ( x ) no ponto x = 0 é
“mais infinito” e denotamos por lim f ( x ) = + ∞ , mas, lembrando que lim f ( x ) não existe.
x →0
x →0
Já para a função g, quando x se aproxima de 3, tanto pela esquerda ( x → 3− ) , quanto pela direita
( x → 3+ ) , os valores da função decrescem ilimitadamente ( g ( x ) → −∞ ) . Neste caso, dizemos que o limite
de g ( x ) no ponto x = 3 é “menos infinito” e denotamos por lim g ( x ) = − ∞ , mas, lembrando que
x →3
lim g ( x ) não existe.
x →3
Utilizamos os símbolos "+ ∞ " e "− ∞ " para ilustrar uma “tendência”, um comportamento
“explosivo”, um aumento modular “ilimitado”. Esses símbolos não são números reais. A maneira precisa de
definirmos esse tipo de tendência de crescimento ilimitado de uma função nas proximidades de um ponto
está dada na seguinte definição.
Definição: Seja f uma função definida num intervalo aberto ( a , b ) , exceto possivelmente em
x = c , c ∈ ( a , b ) . Dizemos que lim f ( x ) = +∞ (respectivamente, − ∞ ) se, para cada M > 0 existe δ > 0 tal
x →c
que f ( x ) > M (respectivamente, f ( x ) < − M ) sempre que 0 < x − c < δ .
Note que lim f ( x ) = +∞ e lim f ( x ) = −∞ apenas indicam o comportamento da função numa
x →c
x →c
vizinhança do ponto c.
1
. Verificamos intuitivamente que
x
quando x tende a 0, o valor f ( x ) tende a +∞ . Pela definição, se nos for apresentado, por exemplo, o
número M = 10 devemos exibir um valor δ > 0 tal que se x ≠ 0 e x ∈ ( −δ , δ ) , então f ( x ) deve ser maior
1
que 10. Para esse valor de M ( M = 10) podemos exibir δ = . Verificamos que se
10
1
1
1
.
0< x < ⇒
> 10 ⇒ f ( x ) > 10 . Se nos for apresentado o número M = 23.117 basta exibir δ =
10
x
23.117
1
1
Verificamos que 0 < x <
⇒
> 23.117 , ou seja, f ( x ) > 23.117 . De maneira geral, conseguimos
23.117
x
mostrar que a definição está satisfeita para qualquer número positivo M apresentado, por maior que ele seja.
1
1
1
Basta exibir δ =
e verificamos que 0 < x < δ =
⇒
> M , ou seja, f ( x ) > M .
M
M
x
Exemplo 17: Para ilustrar a definição considere f ( x ) =
−3
. Intuitivamente percebemos que quando x se
2x − 4
aproxima de 2, pela esquerda ou pela direita, a expressão do denominador se aproxima de zero mediante
números positivos e, portanto, o quociente de −3 por esses números positivos, e cada vez menores, tem um
comportamento “explosivo” para −∞ . Mas esse raciocínio não prova que lim p( x ) = −∞ . É preciso mostrar
Exemplo 18: Considere a função p( x ) =
x →2
que a definição anterior está satisfeita.
Se nos for apresentado, por exemplo, o número M = 20 , devemos exibir δ > 0 tal que
3
0 < x − 2 < δ ⇒ p( x ) < −20 . Nesse caso basta exibir δ =
e teremos
2 ⋅ 20
0 < x −2 <
−3
3
2⋅3
1
20
3
⇒ 0 < 2 x −2 <
⇒
>
⇒
> 20 ⇒
< − 20 .
2 ⋅ 20
2 ⋅ 20
2 x −2
3
2x − 4
2x − 4
Se nos for apresentado o número M = 517π , exibimos δ =
0 < x −2 <
3
. Nesse caso teremos
2 ⋅ 517π
3
2⋅3
1
517π
⇒ 0 < 2 x −2 <
⇒
>
⇒
2 ⋅ 517π
2 ⋅ 517π
2 x −2
3
⇒
−3
3
> 517π ⇒
< − 517π .
2x − 4
2x − 4
Em geral, se nos for apresentado um número M > 0 , tão grande quanto possa ser tomado,
3
e teremos
exibimos δ =
2⋅M
0< x −2 <
3
2⋅3
1
M
3
−3
⇒ 0 < 2 x −2 <
⇒
>
⇒
> M ⇒
< −M .
2⋅ M
2⋅ M
2 x −2
3
2x − 4
2x − 4
Dessa forma, lim
x →2
−3
= −∞ .
2x − 4
Exemplo 19: Considere, agora, a função f ( x ) =
1
cuja representação gráfica é a hipérbole
x
eqüilátera de centro na origem:
7
y
0
x
Observando o gráfico, percebemos que lim f ( x ) = +∞ e
lim f ( x ) = −∞ . Neste caso, dizemos
x →0+
x →0−
que o limite de f ( x ) quando x tende a zero não existe.
Propriedades dos Limites Infinitos
Vamos estudar as principais propriedades dos limites infinitos que permitirão calcular uma grande
quantidade desses limites com maior rapidez. As demonstrações das propriedades enunciadas serão deixadas
como exercícios para o leitor.
Propriedade 1: Se n ∈
a) lim
x →0
+
b) lim
x →0
−
*
, então:
1
= +∞ ;
xn
1  +∞, n par
.
=
x n  −∞, n ímpar
Exemplo 20: Se f ( x ) =
1
1
temos lim f ( x ) = +∞ e lim f ( x ) = +∞ . Portanto, lim 6 = +∞ .
6
x →0
x →0
x →0 x
x
Exemplo 21: Se f ( x ) =
1
temos lim f ( x ) = +∞ e
x →0
x 13
+
−
+
lim f ( x ) = −∞ . Portanto, lim
x →0 −
1
x →0 x 13
não
existe.
Propriedade 2: Se lim f ( x ) = +∞ e lim g ( x ) = k , k ∈
x →c
x →c
, então
a) lim [ f ( x ) ± g ( x ) ] = + ∞ ;
x →c
 +∞, k > 0
b) lim [ f ( x ) . g ( x ) ] = 
.
x →c
 −∞, k < 0
Exemplo 22: Sejam f ( x ) =
1
e g ( x ) = x 2 + 1, . Temos lim f ( x ) = +∞ e lim g ( x ) = 2 ,
x →1
x →1
x −1
então lim [ f ( x ) + g ( x )] = +∞ e lim [ f ( x ) ⋅ g ( x )] = +∞ .
x →1
x →1
1
e g ( x ) = x 3 − 1 . Temos lim f ( x ) = +∞ e lim g ( x ) = −1 , então
x →0
x →0
x8
lim [ f ( x ) + g ( x )] = +∞ e lim [ f ( x ) ⋅ g ( x )] = −∞ .
Exemplo 23: Sejam f ( x ) =
x →0
x →0
Exemplo 24:
Sejam
f (x ) =
1
x
e
g ( x ) = x . Temos lim f ( x ) = +∞ ,
lim g ( x ) = 0 e
x →0
x →0
 1, x > 0
1
lim [ f ( x ) ⋅ g ( x )] não existe. Basta verificar que f ( x ) ⋅ g ( x ) = 
. Considere agora f ( x ) =
e
x →0
x
 −1, x < 0
x2
= 0 . Assim, quando k = 0 ,
x →0
x →0
x →0
x →0 x
no item (b) da propriedade 2, nada se pode concluir a respeito do limite de f ( x ) ⋅ g ( x ) , quando x tende a c.
g ( x ) = x 2 . Temos lim f ( x ) = +∞ , lim g ( x ) = 0 e lim [ f ( x ) ⋅ g ( x )] = lim
Analogamente, temos a seguinte propriedade.
Propriedade 3: Se lim f ( x ) = −∞ e lim g ( x ) = k , k ∈ , então
x →c
x →c
a) lim [ f ( x ) ± g ( x ) ] = − ∞ ;
x →c
 −∞ , k > 0
.
b) lim [ f ( x ) . g ( x ) ] = 
x →c
 +∞ , k < 0
Pode-se construir exemplos análogos aos anteriores para ilustrar essa propriedade. No item b, se
k = 0 nada se pode concluir sobre o limite de f ( x ) ⋅ g ( x ) , quando x tende a c .
Propriedade 4: Se lim f ( x ) = k e lim g ( x ) = 0 , onde k ∈
x →c
x →c
, então
a) Se k > 0 e g ( x ) tende a zero, por valores positivos, então lim
f (x )
= +∞ ;
g( x )
b) Se k > 0 e g ( x ) tende a zero, por valores negativos, então lim
f (x )
= −∞ ;
g( x )
x →c
x →c
c) Se k < 0 e g ( x ) tende a zero, por valores positivos, então lim
f (x )
= −∞ ;
g( x )
d) Se k < 0 e g ( x ) tende a zero, por valores negativos, então lim
f (x )
= +∞ .
g( x )
x →c
x →c
Exemplo 25: Seja f ( x ) = x 2 e g ( x ) = x − 2 . Temos que lim f ( x ) = 4 e lim g ( x ) = 0 , onde
x →2
x →2
f (x )
x2
g ( x ) se aproxima de zero apenas por valores positivos. Logo, lim
= lim
= +∞ .
x →2 g ( x )
x →2 x − 2
Exemplo 26: Seja f ( x ) = 2 x + 1 e g ( x ) = −x 2 . Temos que lim f ( x ) = 1 e lim g ( x ) = 0 , onde
x →0
x →0
f (x )
2x + 1
g ( x ) se aproxima de zero apenas por valores negativos. Logo, lim
= lim
= −∞ .
x →0 g ( x )
x →0 − x 2
Exemplo 27: Seja f ( x ) = 3x 5 + 2 e g ( x ) = x 2 − 1 . Temos que lim f ( x ) = −1 e lim g ( x ) = 0 ,
x →−1
x →−1
f (x )
3x + 2
= lim 2
= −∞ .
1
x
→−
g( x )
x −1
5
onde g ( x ) se aproxima de zero apenas por valores positivos. Logo, lim
x →−1
Exemplo 28: Seja f ( x ) = x 2 − 5 e g ( x ) = − ( x − 2 ) . Temos que lim f ( x ) = −1 e lim g ( x ) = 0 ,
2
x →2
x →2
f (x )
x −5
= lim
= +∞ .
g ( x ) x →2 − ( x − 2 )2
2
onde g ( x ) se aproxima de zero apenas por valores negativos. Logo, lim
x →2
Propriedade 5: Se lim f ( x ) = ±∞ , então lim
x →c
Exemplo 29: Seja f ( x ) =
x →c
x2 −1
( x − 1)
3
1
=0.
f (x )
. Temos que lim f ( x ) = lim
x →1
x →1
x2 −1
( x − 1)
3
= lim
x →1
x +1
( x − 1)2
= +∞ .
( x − 1)
1
Logo, lim
= lim 2
=0.
x →1 f ( x ) x →1 x − 1
3
É importante observar que as cinco propriedades anteriores também são válidas se considerarmos
os limites laterais, quando x → c + ou x → c − .
Exercício 12: Calcule os seguintes limites:
a) lim
x →1+
2x 2 − x − 3
x 2 − 2x + 1
b) lim
1−
t→
2
sen 2 t + cos2 t
2t − 1
c) lim
t →0
2t + 1
t
Limites no Infinito
Na seção anterior estudamos comportamentos “explosivos” de funções f quando a variável
independente, x, se aproxima de algum número real c que pode ou não pertencer ao domínio de f. Estamos
interessados agora em analisar o comportamento de uma função, cujo domínio contenha um intervalo da
forma ( a , +∞ ) ou ( −∞, b ) , quando a variável independente aumenta sua magnitude indefinidamente, quer
com sinal positivo ou com sinal negativo.
Analisemos os casos particulares onde as funções f e h são dadas por
h( x ) =
f (x ) =
−1
+ 3 . Os esboços dos gráficos estão ilustrados a seguir.
x −5
y
1
x
e
y
3
0
0
x
Graf f
5
x
Graf h
Façamos uma exploração numérica do que ocorre com f ( x ) quando de x aumenta
indefinidamente. Façamos também os cálculos de h( x ) quando o módulo de x aumenta indefinidamente,
mas x possui sempre sinal negativo.
x
x
f (x )
h( x )
10
0,1
-10
2.933333333333333
100
0,01
-100
2.990476190476190
1000
0,001
-1000
2.999004975124378
10000
0,0001
-10000
2.999900049975012
100000
0,00001
-100000
2.999990000499975
1000000
0,000001
-1000000
2.999999000004999
Observando os dados apresentados na tabela acima, percebemos que os valores de f ( x ) se
aproximam de zero quando x tende a +∞ , e que os valores de h( x ) se aproximam de 3 quando x tende a
−∞ .
Mas essas considerações numéricas ou a análise do esboço de gráficos não são uma maneira
rigorosa de expressar os comportamentos de funções. Assim como foi feito na seção Limites Infinitos,
daremos a definição com o rigor matemático necessário que expressa esses comportamentos.
Definição: Sejam f uma função definida em ( a , +∞ ) (respectivamente, em ( −∞ , b ) ) e L ∈ .
Dizemos que f ( x ) tende a L quando x tende a +∞ (respectivamente, −∞ ), se dado ε > 0 existe um
número M > 0 tal que f ( x ) − L < ε sempre que x > M (respectivamente, x < − M ). Denotaremos por
lim f ( x ) = L (respectivamente,
x →+∞
lim f ( x ) = L ).
x →−∞
1
= 0 . De fato, se nos for dado um número ε > 0 , por
x →+∞ x
menor que ele seja, devemos exibir M > 0 , suficientemente grande, tal que se x estiver à direita de M
1
( x > M ), então o valor da expressão
deve estar próximo de 0, distando dele no máximo ε unidades.
x
Exemplo 30: Vamos mostrar que lim
Estudaremos uma situação particular onde nos é dado o número ε = 0, 01 . Nesse caso, tomando
M = 100 , teremos
x > 100 ⇒
ε = 10
−23
1
1
1
<
⇒ − 0 < 0, 01 .
x 100
x
Vamos supor que nos seja dado o número ε > 0 muito menor que o anterior, por exemplo
. Nesse caso, basta tomar M = 10 23 e teremos
x > 10 23 ⇒
1
1
< 10 −23 ⇒ − 0 < 10 −23 .
x
x
Ora, dado o número ε > 0 , por menor que seja ele, tomando o número M =
x>
Assim mostramos que lim
x →+∞
1
ε
⇒
1
1
<ε ⇒ −0 <ε .
x
x
1
= 0.
x
Exercício 13: Mostre, utilizando a definição, que lim
x →−∞
−1
+ 3=3.
x −5
Propriedade:
a) lim
x → ±∞
1
= 0 , n∈
xn
*
;
−∞, m < 0

b) Se m e b são constantes, então lim ( mx + b ) =  b , m = 0 .
x →+∞
+∞, m > 0

Exemplo 31: lim
x →+∞
1
=0 e
x7
lim
x →−∞
1
=0.
x7
1
ε
, temos
Exemplo 32:
lim ( 3x + 9 ) = +∞ e
x →+∞
lim ( 3x + 9 ) = −∞ .
x →−∞
5 
5 


x2 3 + 2 
3+ 2 

3x + 5
x 
x 

Exemplo 33: lim
= lim
= lim 
= −3
x →+∞ 2 − x 2
x →+∞ 2  2
x
→+∞

 2

x  2 − 1
 2 − 1
x

x

2
Os limites no infinito têm propriedades análogas às propriedades de limites vistas nas seções
anteriores.
Exercício 14: Calcule os seguintes limites:
1

a) lim  x + 
x →+∞
x

b) lim
x →−∞
x2 + 3
2x + 1
2x + 1
x →−∞ x + 2
c) lim
3x 2 + 9 x
x →+∞ 2 x + 3
d) lim
Assíntotas
Assíntota Vertical
A idéia de limites laterais infinitos possibilita introduzir o conceito de assíntota vertical do gráfico
de uma função.
Definição: Seja f uma função definida num intervalo aberto ( a , b ) , exceto possivelmente em
x = c , c ∈ ( a , b ) . Dizemos que a reta x = c é uma assíntota vertical do gráfico de f, se pelo menos uma das
seguintes condições ocorrer:
a) lim f ( x ) = + ∞
x →c +
b) lim f ( x ) = − ∞
x →c +
c) lim f ( x ) = + ∞
x →c −
d) lim f ( x ) = − ∞ .
x →c −
Geometricamente, a assíntota vertical do gráfico de uma função f é a reta paralela ao eixo Oy que
−1
passa pelo ponto ( c , 0) . A figura a seguir ilustra o gráfico da função h( x ) =
+ 3 e sua assíntota vertical,
x −5
a reta de equação x = −5 .
y
3
0
5
x
f (x )
, onde f e g são funções polinomiais, as
g( x )
assíntotas verticais de seu gráfico, caso existam, ocorrem em valores de c tais que g ( c ) = 0 .
Caso a função seja racional, isto é, da forma F ( x ) =
Exemplo 34: Dadas as funções abaixo definidas, vamos verificar se seus gráficos possuem
assíntotas verticais.
6
;
4−x
b) f ( x ) =
−2
;
( x − 1)2
c) f ( x ) =
x +2
;
( x − 2)3
 −1
 , x <0
d) f ( x ) =  x
;
 3x , x ≥ 0
e) f ( x ) =
1
;
1 − 2x
f) f ( x ) =
x2 + x − 2
.
x −1
a) f ( x ) =
Para determinar as assíntotas verticais, pela definição, calculemos os seguintes limites:
a) lim
6
= +∞ e assim, por definição, a reta x = 4 é uma assíntota vertical do gráfico de f ;
4−x
b) lim
−2
= −∞ e assim, por definição, a reta x = 1 é uma assíntota vertical do gráfico de f ;
( x − 1)2
c) lim
x +2
= −∞ e assim, por definição, a reta x = 2 é uma assíntota vertical do gráfico de f ;
( x − 2)3
x →4 −
x →1−
x → 2−
d) lim− f ( x ) = lim−
x →0
x →0
−1
= +∞ e, assim, por definição, a reta x = 0 é uma assíntota vertical do
x
gráfico de f ;
e) lim−
x →0
f)
1
= +∞ e assim, por definição, a reta x = 0 é uma assíntota vertical do gráfico de f ;
1 − 2x
x2 + x − 2
( x − 1)( x + 2)
= lim
= lim( x + 2) = 3 , o gráfico de f
x →1
x
→
1
x →1
x −1
x −1
Como lim
assíntota vertical.
não possui
Assíntota Horizontal
A idéia de limite no infinito permite definir assíntota horizontal do gráfico de uma função cujo
domínio contém um intervalo do tipo ( a , +∞ ) ou ( −∞, b ) .
Definição: Dizemos que a reta y = k é uma assíntota horizontal do gráfico de uma função f , se
lim f ( x ) = k ou
x →+∞
lim f ( x ) = k .
x →−∞
Geometricamente, a assíntota horizontal do gráfico de uma função f é a reta paralela ao eixo Ox
−1
que passa pelo ponto (0, k ) . A figura anterior ilustra o gráfico da função h( x ) =
+ 3 e sua assíntota
x +5
horizontal, a reta de equação y = 3 .
Exemplo 35: Dadas as funções abaixo definidas, vamos verificar se seus gráficos possuem
assíntotas horizontais.
a) f ( x ) =
1
+3 ;
x
 3
 x − 1 , x < 1
d) f ( x ) = 
;
 1 + 1, x ≥ 1
 x
b) f ( x ) =
−3
;
2
x −3
e) f ( x ) =
c) f ( x ) =
1 − 3x 2 − x
;
7 − 5x 2
5x 2 + 1
.
2x − 3
Para determinar as assíntotas horizontais, por definição, devemos calcular os seguintes limites:
1

1

a) lim  + 3  = 3 e lim  + 3  = 3 . Assim, por definição, a reta y = 3 é uma assíntota
x →+∞ x
x →−∞ x




horizontal do gráfico de f ;
−3
−3
= 0 e lim
= 0 . Assim, por definição, a reta y = 0 é uma assíntota
2
x →+∞ x − 3
x →−∞ x − 3
horizontal do gráfico de f ;
b)
lim
2
1 − 3x 2 − x
3
1 − 3x 2 − x
3
=
e
lim
= . Assim, por definição, o gráfico de f tem a
2
2
x →+∞
x →−∞
5
5
7 − 5x
7 − 5x
3
reta y = como assíntota horizontal;
5
c) lim
1

 3 
d) lim f ( x ) = lim  + 1  = 1 e lim f ( x ) = lim 
 = 0 . Assim, por definição, as retas
x →+∞
x →+∞  x
x →−∞
x →−∞  x − 1 

y = 1 e y = 0 são assíntotas horizontais do gráfico de f ;
5x 2 + 1
5x 2 + 1
= + ∞ e lim
= − ∞ . Assim o gráfico de f não possui assíntota
x →+∞ 2 x − 3
x →−∞ 2 x − 3
horizontal.
e) lim
Exercícios
15. Determinar, caso existam, as assíntotas verticais e horizontais dos gráficos das funções
definidas a seguir:
4x 3 + x 2
;
x −3
a) f ( x ) =
2x
;
2
x − 25
b) f ( x ) =
d) f ( x ) =
5 − 3x
;
4x 6 + 5
 1
x <0
 x ,
e) f ( x ) = 
.
 2 − 2, x ≥ 0
 x + 1
5
c) f ( x ) =
2
+3 ;
x
16. Dê um exemplo de função que possua duas assíntotas horizontais diferentes.
O Limite Fundamental
As indeterminações ocorrem também quando trabalhamos com funções trigonométricas. Para estas
situações o resultado a seguir ajuda a resolver muitas delas.
lim
x →0
De fato, tomemos, inicialmente, 0 < x <
π
sen x
= 1
x
. Na figura a seguir, P I é um arco de medida x de uma
2
circunferência de raio 1; PQ e TI são perpendiculares ao eixo horizontal.
y
1
-1
P
T
Q
I
O
x
Denotaremos por ∆ABC um triângulo com vértices A, B e C.
Temos que
Área do ∆ IOP < Área do setor circular IOP < Área do ∆ IOT.
(1)
Como OI = OP = 1 segue que
Área do ∆IOP =
1
1
⋅ PQ ⋅ OI =
⋅ PQ
2
2
Área do setor circular IOP =
Área do ∆ IOT =
2
1
1
⋅ x ⋅ OP = ⋅ x
2
2
1
1
⋅ IT ⋅ OI = ⋅ IT
2
2
(2)
(3)
(4)
Por outro lado, sabemos que:
sen x =
PQ
= PQ
OP
(5)
tg x =
IT
= IT .
OI
(6)
Substituindo (2), (3), (4), (5) e (6) em (1) obtemos
1
1
1
sen x < x < tg x
2
2
2
que é equivalente a
1<
x
1
,
<
sen x
cos x
ou seja,
cos x <
sen x
< 1
x
(7)
π
Como 0 < x <
2
, temos que 0 < sen x < x e como a função F ( x ) = x 2 é crescente, para
2
x > 0 , temos que 0 < sen 2 x < x 2 , ou ainda, sen 2
trigonométrica sen 2 θ =
x
x2
x 
<   =
. Dessa desigualdade e da igualdade
2
4
2
1 − cos 2θ
x2
x 
segue que cos x = 1 − 2 sen 2   > 1 − 2
. Assim, obtemos que
2
4
2
cos x > 1 −
x2
2
(8)
Utilizando (7) e (8), obtemos
1−
sen x
x2
π
<
< 1 , para 0 < x < .
2
x
2
 x2
Como lim  1 −
x →0
2


sen x
= 1.
 = 1 e lim 1 = 1 , segue do Teorema do Confronto que lim
x →0
x →0
x

Aqui tomamos
x > 0 , entretanto, a função
+
f (x ) =
sen x
x
é uma função par, pois
sen ( − x )
−sen x
sen x
=
=
= f ( x ), ∀x ≠ 0 . Portanto, temos também que
−x
−x
x
sen x
Logo, lim
=1.
x →0 x
f ( −x ) =
lim
x →0−
sen x
= 1.
x
Existe um outro limite bastante importante, cuja existência não será demonstrada neste texto, a
saber,
x
1

lim  1 +  = e
x →∞ 
x
O número irracional e transcendente “e” obtido com o cálculo desse limite é denominado número
de Napier ou número de Euler e tem como valor aproximado 2,71828.
Exercício 17: Calcule os limites a seguir:
a) lim
h→0
d)
lim
x →+∞
g) lim
x →9
sen(2h )
h
b) lim
x →0
x
x+ x+ x
x −3
3−x
e)
lim
x →+∞
sen 3 x
x3
x 2 − 5x + 6
3
h) lim
x →7
x −37
x −7
c)
f)
lim
x →2
+
x +2
2−x
lim ( x ( x + a ) − x )
x →+∞
3x 2 + 9x − 12
x →−4 17x − 4 x 2 − 4
i) lim
−3
j) lim
x →3+
x2 − 9
l) lim
2 x 2 − 6x + 1
x →+∞ 5x + 7x 2 + 4
o) lim
x 3 − 27x
x →−∞ x 2 − 5x + 8
r) lim
sen(4 x )
x →0
x
u) lim
4 − 3x
x →−∞ 2 x 2 + 1
n) lim
7x 3 − 4 x + 8
x →−∞ 2 x 2 − x − 1
q) lim
x +1
x →+∞ 2 + 3x 2 − 5 x
t) lim
m) lim
p) lim
s) lim
v) lim
x →π
y)
2 + x − x2
x → 2 3x 2 − 6 x
+
sen x
x −π
2

lim  1 + 
x →+∞ 
x
3x 2 + 5
x →+∞ 4 x 2 − 1
k) lim
x) lim
x →0
x +1
z)
2x − x 4
x →+∞ x 5 + 4 x
3 + x − x2
x →−∞ x 2 + 5
sen 3 (2 x )
x →0
x3
cos(π x 3 )
x → −∞ x 3 + 5
sen(2 x )
4x
1 

lim  1 +

x →+∞ 
2x 
w) lim
x
Continuidade
Assim como o conceito de limite desempenha papel importante, o conceito de continuidade é
fundamental na matemática e em outras ciências, e é uma das idéias centrais do Cálculo.
Como a representação gráfica de uma função tem a vantagem de transmitir informações locais e
globais sobre o comportamento da função em um dado intervalo, vamos ver qual é a característica gráfica que
explicita o desejado conceito intuitivo de “continuidade” de uma função num ponto.
Nas ilustrações a seguir apresentamos três gráficos: o de uma função f e o de uma função g e o
de uma função h, definidas em toda a reta real .
y
y
y
8
6
6
3
x
0
0
Graf f
5
0
x
Graf g
x
5
Graf h
Percebemos que nas proximidades do ponto de abscissa x = 5 o gráfico de g e o gráfico de h
apresentam uma particularidade que não existe no gráfico de f : lim− f ( x ) = lim+ f ( x ) = f (5) ; lim+ g ( x ) = 8
x →5
e lim− g ( x ) = 6 ; lim+ h( x ) = lim− h( x ) = 6 ≠ 3 = h (5) .
x →5
x →5
x →5
x →5
x →5
As funções que apresentam comportamento similar ao da f , ou seja, lim f ( x ) = lim f ( x ) = f ( c )
x →c −
são chamadas de contínuas no ponto x = c , e são o objeto de estudo nesta seção.
x →c +
Definição: Sejam f uma função definida num intervalo aberto ( a , b ) e c ∈ ( a , b ) . Dizemos que f é
contínua no ponto x = c se, lim f ( x ) = f ( c ) .
x →c
Uma definição equivalente a essa, utilizando ε e δ , é apresentada a seguir.
Definição: Sejam f uma função definida num intervalo aberto ( a , b ) e c ∈ ( a , b ) . Dizemos que f é
contínua em x = c se dado ε > 0 existe δ > 0 tal que
x ∈( a , b ) .
f ( x ) − f ( c ) < ε sempre que x − c < δ para
O primeiro passo agora é provar que as duas definições apresentadas são equivalentes. Isto é, toda
função que é contínua segundo uma definição também é contínua segundo a outra definição.
Vamos inicialmente provar que a segunda definição implica na primeira definição.
De fato, dado ε > 0 existe δ > 0 tal que se x ∈ ( c − δ , c + δ ) ∩ ( a , b ) tem-se | f ( x ) − f ( c )| < ε .
Como existe x ∈ ( c − δ , c + δ ) ∩ ( a , b ) = I , pois I é um intervalo, temos que | f ( x ) − f ( c )| < ε . Assim,
por definição, tem-se lim f ( x ) = f ( c ) .
x →c
Agora, vamos mostrar que a primeira definição implica na segunda definição.
k∈
*
Suponha que a função f não satisfaça a segunda definição. Então, existe ε > 0 tal que para cada
podemos obter x k ∈ ( a , b ) com | x k − c | < k1 e | f ( x k ) − f ( c )| ≥ ε . Desse modo, obtemos
um conjunto de pontos de ( a , b ) cujos elementos se aproximam de c, sem que a função, nesses pontos, se
aproxime de f(c) . Isso contradiz a hipótese.
Se a função for definida num intervalo fechado [ a , b ] , ainda é possível definir continuidade nos
extremos desse intervalo como segue.
Definição: Seja f uma função definida num intervalo fechado[ a , b ] . Dizemos que f é :
a) contínua à esquerda no ponto x = b se, e somente se, lim− f ( x ) = f ( b ) .
x →b
b) contínua à direita no ponto x = a se, e somente se, lim+ f ( x ) = f ( a ) .
x →a
Dizemos que uma função f é contínua em um intervalo fechado [ a , b ] se ela for contínua em todos
os pontos do intervalo aberto ( a , b ) , e contínua à direita em x = a e à esquerda em x = b .
Quando uma função não for contínua em um dos pontos de seu domínio diremos que ela é
descontínua nesse ponto. A continuidade de uma função em um ponto é uma propriedade local da função.
As funções g e h cujos gráficos foram exibidos no início desta seção são descontínuas em x = 5 .
A função g é descontínua em x = 5 porque não existe o lim g ( x ) e a função h é descontínua em x = 5 ,
x→5
pois embora exista lim h( x ) , seu valor é diferente de h(5) .
x→5
Exemplo 36:Uma copiadora publicou a seguinte tabela de preços:
Número de cópias de um mesmo original
Preço por cópia
de 1 a 19
R$ 0,10
de 20 a 49
R$ 0,08
50 ou mais
R$ 0,06
Um estudante de matemática apresentou uma função que associa a cada número de cópias n o
valor a ser pago: f : → é dada por.
0,10 n , 1 ≤ n ≤ 19

f ( n ) = 0, 08 n , 20 ≤ n ≤ 49 .
0, 06 n , n ≥ 50

Consideremos agora a função F dada por
0 ≤ x < 20
0,10 x ,

F ( x ) =  0, 08 x , 20 ≤ x < 50
 0, 06 x ,
x ≥ 50

que coincide com a função f quando os valores de x são números naturais. O esboço do seu gráfico é
apresentado a seguir.
F(x)
4,0
3,0
2,0
1,6
0
20
50
x
Observe que o gráfico não é contínuo. Veja, por exemplo, tirar 20 ou 50 cópias é mais
vantajoso do que tirar 19 ou 49, respectivamente. Para que a função deixe de provocar tais
distorções, a tabela deve ser reformulada de modo a se definir uma nova função G : + → , tal
que seu gráfico não apresente “saltos” ou “depressões”. A função G : + → , pode ser dada por
0 ≤ x < 20
 0,10 x ,

G( x ) = 0, 08 x + 0, 40, 20 ≤ x < 50
 0, 06 x + 1, 40,
x ≥ 50

Agora a função G é contínua em seu domínio. Deixamos para o leitor a verificação desta afirmação.
Exercícios
18. Prove que a função f ( x ) = x 5 + 6x + 2 é contínua para todo x ∈
.
x ≠0
8 x ,

19. Dada a função f ( x ) =  1
, determine seus pontos de descontinuidade, se existirem.
 10 23 , x = 0
−5,
x − 2,

20. Estude a continuidade da função f ( x ) =  3
x ,
10,

x = −3
−3 < x < 0
0≤x <3
x =3
.
Exemplo 37: A função f ( x ) = sen x é contínua em x = 0 .
De fato, queremos mostrar que lim sen x = sen 0 = 0 . Como x ≠ 0 , temos que sen x = x
x →0
Assim,
sen x 
sen x

lim sen x = lim  x ⋅
= lim x ⋅ lim
= 0 ⋅ 1 = 0 = sen 0 .

x →0
x →0 
x  x → 0 x →0 x
Logo, f é contínua em x = 0 .
Exemplo 38: A função f ( x ) = cos x é contínua em x = 0 .
De fato, como cos x = 1 − sen 2 x para valores de x próximos de 0, segue que
lim cos x = lim 1 − sen 2 x =
x →0
x →0
Logo, f é contínua em x = 0 .
(
lim 1 − sen 2 x
x →0
)
= 1 = 1 = cos 0 .
sen x
.
x
Exemplo 39: Vamos mostrar que lim
x →0
1 − cos x
= 0.
x
De fato,
lim
x →0
(1 − cos x ) (1 + cos x )
1 − cos x
1 − cos 2 x
= lim
= lim
=
x →0
x → 0 x ( 1 + cos x )
x
x (1 + cos x )
= lim
x →0
Logo, lim
x →0
sen x
sen 2 x
senx
= lim
. lim
= 1. 0 = 0.
0
0
x
→
x
→
1 + cos x
x ⋅ (1 + cos x )
x
1 − cos x
=0
x
Exemplo 40: A função f ( x ) = sen x é contínua.
Queremos mostrar que lim sen x = sen c , para todo c ∈
x →c
.
De fato, fazendo a mudança de variável x = t + c , temos que
lim sen x = lim sen ( t + c ) = lim ( sen t .cos c + sen c .cos t ) =
x →c
t →0
t →0
= lim ( sen t ⋅ cos c ) + lim ( sen c ⋅ cos t ) =
t →0
t →0
= cos c ⋅ lim sen t + sen c ⋅ lim cos t = cos c ⋅ 0 + sen c ⋅ 1 = sen c .
t →0
t →0
Logo, lim sen x = sen c . Portanto, a função seno é contínua em
x →c
.
Exercícios
21. Mostre que a função f ( x ) = cos x é contínua.
22. Calcule os limites a seguir:
a) lim
x →0
d) lim
x →1
tg x
;
2x
b) lim
1− x
;
πx 
tg 

 2 
e) lim
t →0
x →0
t
;
cos t − 1
tg 4 (2 x )
;
x4
c) lim
x2
;
1 − 2 cos 2 x
f) lim
x
.
1 − cos x
x →0
x →0
Propriedades: Sejam f e g funções definidas no intervalo [ a , b ] . Se f e g são contínuas em
c ∈ [ a , b ] , então:
(a) f + g , f − g e f ⋅ g são funções contínuas em c ;
(b) f / g é função contínua em c , se g ( c ) ≠ 0 .
A demonstração dessas propriedades segue das propriedades de limites. Essas propriedades
possibilitam afirmar que uma função é contínua ou não sabendo apenas se as partes que a compõem são ou
não contínuas. Vejamos alguns exemplos.
Exemplo 41: A função f ( x ) =
x 5 + 2x + 1
é contínua em todos os pontos de seu domínio.
x2 −1
De fato, a função identidade y( x ) = x é contínua em qualquer ponto a ∈ , pois
lim y( x ) = lim x = a = y ( a ) . A função constante y( x ) = 1 também é contínua em todo a ∈ , pois
x →a
x →a
lim y( x ) = lim 1 = 1 = y ( a ) . Pelo item a da propriedade anterior as funções
x →a
x →a
y( x ) = x 2 e y( x ) = −1 são contínuas em qualquer ponto a ∈
y( x ) = x 5 ,
y( x ) = 2x ,
. Novamente, mediante o uso do item a,
concluímos que as funções y( x ) = x 5 + 2 x + 1 e y( x ) = x 2 − 1 são contínuas em qualquer ponto a ∈ .
Utilizando, agora, o item b, concluímos que a função f é contínua em todos os pontos de
que não sejam
zeros de y( x ) = x 2 − 1 , ou seja, f é contínua em todos os pontos do conjunto
− {−1,1} = Dom f .
Exercícios
23. Demonstre os seguintes teoremas:
a) Se f é um polinômio, então f é contínua para x ∈
.
b) Se f é uma função racional, então f é contínua em todos os pontos onde não se anula o
denominador.
24. Dadas as funções definidas por y = f ( x ) a seguir, verifique se f é contínua nos pontos
x = a e x = b indicados.
x 2 − 7,
x < −1

a) f ( x ) = −6,
−1 ≤ x ≤ 2 ,
2 − 4 x ,
x > 2

1 − x 2 ,

b) f ( x ) = 4 − 2 x ,
3 − x ,

x < −3
− 3 ≤ x ≤ 1,
x > 1
( a = − 1, b = 2)
( a = −3, b = 1)
25. Mostre que as funções trigonométricas tg x, sec x, cotg x e cossec x são contínuas.
Falta-nos, até esse momento, um resultado acerca da continuidade de uma composição de funções
que enunciaremos e demonstraremos a seguir.
Proposição: Sejam as funções f :[ a , b ] → e g :[ c , d ] →
com Im f ⊂ [ c , d ] . Se f é contínua
em x 0 ∈[ a , b ] e g é contínua em y 0 = f ( x 0 ) , então a função composta ( g o f ) :[ a , b ] → é contínua em
x0 .
Demonstração:
A
função
go f
está
definida
no
ponto
x0 ∈ [a,b ]
e
( g o f )( x 0 ) = g ( f ( x 0 )) = g ( y 0 ) . Precisamos mostrar que ( g o f ) é contínua em x 0 , isto é, que dado
ε > 0 existe δ > 0 tal que se | x − x 0 | < δ , então |( g o f )( x ) − ( g o f )( x 0 )| < ε .
Como g é contínua em y 0 , dado ε > 0 existe δ
1
> 0 tal que se
y − y 0 < δ 1 , então
g ( y ) − g ( y 0 ) < ε . Como f é contínua em x 0 , para o δ 1 > 0 , que existe da continuidade de g , existe
δ
2
> 0 tal que se | x − x0 | < δ 2 , então f ( x ) − f ( x 0 ) < δ 1 . Agora, como f ( x ) − f ( x 0 ) < δ 1 ,
então
podemos concluir que g ( f ( x )) − g ( f ( x 0 )) < ε . Isto é, ( g o f ) é contínua em x 0 .
Apresentaremos a seguir os enunciados de dois teoremas que são fundamentais para o
desenvolvimento do Cálculo Diferencial e Integral, porém suas demonstrações serão omitidas neste texto.
Teorema (do Valor Intermediário): Se f é uma função contínua em [ a , b ] e se f ( a ) ≠ f ( b ) ,
então para todo k entre f(a) e f(b) existe pelo menos um c ∈ ( a , b ) tal que f ( c ) = k .
Exemplo 42: Considere a função f ( x ) = x 2 − 5 definida no intervalo [ 2, 3 ] . Como esta função é
contínua neste intervalo e, além disso, f (2) = −1 e f (3) = 4 , o teorema acima garante que, qualquer que seja
o número k , escolhido entre −1 e 4, existe um número c, entre 2 e 3, tal que f ( c ) = k , isto é, a equação
c 2 − 5 = k tem solução no intervalo ( 2, 3 ) qualquer que seja o número k entre −1 e 4. Por exemplo, se
escolhemos k = 0 , observamos que f ( 5 ) = 0 e
5 ∈ ( 2, 3 ) .
Teorema (do Anulamento ou de Bolzano): Se f é uma função contínua em [ a , b ] e se f ( a ) e
f ( b ) têm sinais contrários, então existe pelo menos um c ∈ ( a , b ) tal que f ( c ) = 0 .
Exemplo 43: A função f ( x ) = 3x 3 − 6x + 2 tem pelo menos uma raiz entre 1 e 2. De fato, como
f é contínua em [ 1, 2 ] e f (1) = − 1 e f (2) = 14 , existe pelo menos um c ∈ ( 1, 2 ) tal que f ( c ) = 0 .
Teorema (Conservação de sinal): Seja f uma função contínua em x = c , c ∈ ( a , b ) tal que
f ( c ) > 0 . Então, existe δ > 0 tal que se x ∈ ( c − δ , c + δ ) , então f ( x ) > 0 .
Demonstração: Como
f é contínua em c ∈ ( a , b ) , dado ε > 0 , existe δ > 0 tal que se
x − c < δ , então f ( x ) − f ( c ) < ε , ou seja, −ε < f ( x ) − f ( c ) < ε . Assim, se x − c < δ tem-se
f ( c ) − ε < f ( x ) < f ( c ) + ε . Tomando ε ≤ f ( c ) tem-se que 0 < f ( x ) < f ( c ) + ε . Portanto,
f ( x ) > 0 , para todo x satisfazendo x − c < δ .
Exercício 26: Enuncie e demonstre o teorema da conservação de sinal, considerando f ( c ) < 0 .
Teorema (Continuidade da função inversa): Seja f uma função crescente e contínua em [ a , b ] .
Se a imagem de f é o intervalo [ c , d ] , onde c = f ( a ) e d = f ( b ) , então a função inversa
f −1 :[ c , d ] → [ a , b ] é crescente e contínua.
Demonstração: Vamos mostrar inicialmente que Im f = [ c , d ] . Como f é crescente, temos que
f ( a ) < f ( b ) . Além disso, como f é contínua, segue do Teorema do Valor Intermediário que para todo
f ( a ) < y < f ( b ) , existe um único x ∈ ( a , b ) tal que y = f ( x ) . Tomando f ( a ) = c e f ( b ) = d , temos o
desejado. Mostremos agora que f −1 é crescente em [ c , d ] . Como f −1 está definida em [ c , d ] , tomemos
tal que y1 < y 2 . Seja x 1 = f −1 ( y1 ) e x 2 = f −1 ( y 2 ) . Para demonstrar o desejado,
y1 , y 2 ∈ [ c , d ]
devemos mostrar que x 1 < x 2 . Suponhamos que x 1 ≥ x 2 . Como f é crescente, tem-se que f ( x 1 ) ≥ f ( x 2 ) ,
isto é, y1 ≥ y 2 , o que é uma contradição. Logo, x 1 < x 2 e assim f −1 é crescente em [ c , d ] . Para concluir
a demonstração, mostremos que f −1 é contínua em [ c , d ] . Queremos mostrar que:
(1) lim f −1 ( y ) = f −1( y 0 ) , se y 0 ∈ ( c , d ) ;
y → y0
(2) lim+ f −1 ( y ) = f −1 ( c ) ;
y →c
(3) lim− f −1 ( y ) = f −1( d ) .
y →d
Vamos demonstrar (1): Seja x 0 ∈ ( a , b ) tal que
y 0 ∈ ( c , d ) ), ou equivalentemente, x 0 = f
−1
f ( x 0 ) = y 0 (existe, pois Im f = [ c , d ] e
( y 0 ) . Assim, devemos mostrar que dado ε > 0 existe δ > 0 tal
que f −1( y ) − f −1( y 0 ) < ε sempre que y − y 0 < δ . Como a função f é contínua, podemos escolher
δ > 0 de modo que
( y0 − δ , y0 + δ )
⊂
( f ( x 0 − ε ),
f ( x 0 + ε )) .
Para isto, basta tomar δ = min{ f ( x 0 ) − f ( x 0 − ε ); f ( x 0 + ε ) − f ( x 0 )} .
Porém,
y − y0 < δ ⇒ y0 − δ < y < y0 + δ ⇒ f ( x 0 − ε ) < y < f ( x 0 + ε ) .
Como f −1 é crescente, podemos escrever:
f −1 ( f ( x 0 − ε )) < f −1 ( y ) < f −1 ( f ( x 0 + ε ) ) ⇒ x 0 − ε < f −1( y ) < x 0 + ε ⇒
f −1 ( y 0
) −ε
< f −1( y ) < f −1 ( y 0 ) + ε ⇒
f −1( y ) − f −1( y 0 ) < ε .
Logo, lim f −1 ( y ) = f −1( y 0 ) , se y 0 ∈ ( c , d ) . Demonstraremos, agora, (2), ou seja, que f −1 é
y → y0
contínua em c . Dado ε > 0 , devemos mostrar que existe δ > 0 tal que f −1( y ) − f −1( c ) < ε sempre que
0 < y − c < δ . Como a função f é contínua e crescente, podemos escolher δ > 0 de modo que
(c , c + δ )
⊂ ( a , f ( a + ε )) .
para isto, basta tomar por exemplo, δ = f ( a + ε ) − c . Porém,
0 < y − c < δ ⇒ c < y < c + δ ⇒ c < y < f (a + ε ) .
Como f −1 é crescente, podemos escrever:
f −1 ( c ) < f −1 ( y ) < f −1 ( f ( a + ε ) ) ⇒ f −1 ( c ) < f −1( y ) < a + ε ⇒
⇒ f −1 ( c ) < f −1( y ) < f −1 ( c ) + ε ⇒ f −1( y ) − f −1( c ) < ε
Assim, lim+ f −1 ( y ) = f −1 ( c ) . Deixamos como exercício a demonstração de (3), ou seja, que f −1 é
y →c
contínua em d.
Corolário: Se n é um inteiro positivo e f ( x ) = n x , então:
a) se n é ímpar, f é contínua para todo número real;
b) se n é par, f é contínua para todo número não negativo.
Demonstração: Basta observar que a função f ( x ) = n x é contínua, pois é a função inversa da
função g ( x ) = x n restrita a um domínio apropriado, onde é crescente.
a) Se n é ímpar, g é crescente em
temos a continuidade de f .
e assim, pelo Teorema da Continuidade da Função Inversa,
b) Se n é par, g é crescente para todo número não negativo e novamente pelo Teorema da
Continuidade da Função Inversa, temos a continuidade de f para este n .
Exemplo 44:
novamente:
Agora é possível demonstrar duas propriedades de limites que enunciaremos
Seja f uma função cujo domínio contém o intervalo ( a , b ) e c ∈ ( a , b ) . Se lim f ( x ) = L , então:
x →c
n
a) lim
x →c
b) lim
n
x →c
f (x ) =
f (x ) =
n
n
L , se n é um número natural ímpar;
L , se n é número natural par não-nulo e L ≥ 0 .
Consideremos a função h definida por h( x ) = n x . Então, a função composta h o f é definida por
h o f ( x ) = h( f ( x )) = n f ( x ) . Segue da continuidade da composta e do corolário acima que h o f é
contínua em c se n é ímpar, ou se n é par não-nulo e L ≥ 0 . Logo,
lim
x →c
L ≥ 0.
n
(
)
f ( x ) = lim h( f ( x )) = h lim f ( x ) = h ( L ) =
x →c
x →c
n
L se n é ímpar, ou se n é par não-nulo e
Teorema (de Weierstrass): Se f é uma função contínua em [ a , b ] , então existem x 1 , x 2 ∈ [ a , b ]
tais que f ( x 1 ) ≤ f ( x ) ≤ f ( x 2 ) , para todo x ∈ [ a , b ] .
No teorema anterior, o valor f ( x 1 ) é chamado mínimo absoluto de f em [ a , b ] e f ( x 2 ) é
chamado valor máximo absoluto de f em [ a , b ] . Estes conceitos serão abordados com detalhes quando
estudarmos as derivadas.
Exercícios
27. Dado o gráfico de uma função y = f ( x ) a seguir, determine o que se pede, se possível:
y
4
3
2
1
–5
–3 –2
–1 0 1
2
4
x
6
a) Dom f
b) Im f
c) f (0)
d) f ( −2)
e) f (2)
f) f ( 5 )
g) f ( 7 )
h) f ( f (0))
i) lim f ( x )
j) lim f ( x )
l) lim f ( x )
m) lim f ( x )
n) lim f ( x )
o)
p) lim f ( x )
q) lim f ( x )
r) lim f ( x ) s)
s) lim
t) lim f ( x )
u) lim f ( x )
x→0
x →1+
x → 11
x →−2−
lim f ( x )
x → −1−
x → −5−
f (x )
x →−2+
x →+∞
x→ 5
x →2
x →−∞
x → 11
28. Com base nas respostas acima, responda:
(a) f é contínua em x = −5, − 2, − 1, 2, 0, 5 , 11 ?
(b) A reta x = 5 é uma assíntota vertical do gráfico de f ? Justifique sua resposta.
(c) Quais as assíntotas horizontais e verticais do gráfico de f ?