Cálculo I
Humberto José Bortolossi
Departamento de Matemática Aplicada
Universidade Federal Fluminense
Aula 21
6 de novembro de 2008
Aula 21
Cálculo I
1
Convexidade, concavidade e pontos de
inflexão
Aula 21
Cálculo I
2
O que estas funções têm de diferente?
y
gráfico de f
0
x
y
gráfico de f
0
Aula 21
x
Cálculo I
3
Convexidade (concavidade para cima)
Definição
Dizemos que uma função f definida em um intervalo I é convexa
(ou côncava para cima), se o segmento de reta secante que passa
pelos pontos (p, f (p)) e (q, f (q)) sempre está acima ou coincide com
o gráfico de f para qualquer escolha de pontos p e q em I.
y
f(p)
seg
me
nto
de r
eta
sec
ant
gráfico de f
e
f(q)
0
Aula 21
p
q
x
Cálculo I
4
Concavidade (concavidade para baixo)
Definição
Dizemos que uma função f definida em um intervalo I é côncava (ou
côncava para baixo), se o segmento de reta secante que passa pelos
pontos (p, f (p)) e (q, f (q)) sempre está abaixo ou coincide com o
gráfico de f para qualquer escolha de pontos p e q em I.
y
f(q)
seg
me
n
e
to d
ret a
sec
ant
e
gráfico de f
f(p)
0
Aula 21
p
q
x
Cálculo I
5
Convexidade e concavidade em intervalos
Teorema
Seja I um intervalo contido no domínio de uma função f . Suponha
que f , f 0 e f 00 sejam contínuas em I.
(1) Se f 00 (x) > 0 para todo x ∈ I, então f é uma função
côncava para cima no intervalo I.
(2) Se f 00 (x) < 0 para todo x ∈ I, então f é uma função
côncava para baixo no intervalo I.
Aula 21
Cálculo I
6
Convexidade e concavidade em intervalos
Teorema
Seja I um intervalo contido no domínio de uma função f . Suponha
que f , f 0 e f 00 sejam contínuas em I.
(1) Se f 00 (x) > 0 para todo x ∈ I, então f é uma função
côncava para cima no intervalo I.
(2) Se f 00 (x) < 0 para todo x ∈ I, então f é uma função
côncava para baixo no intervalo I.
Aula 21
Cálculo I
7
Convexidade e concavidade em intervalos
Teorema
Seja I um intervalo contido no domínio de uma função f . Suponha
que f , f 0 e f 00 sejam contínuas em I.
(1) Se f 00 (x) > 0 para todo x ∈ I, então f é uma função
côncava para cima no intervalo I.
(2) Se f 00 (x) < 0 para todo x ∈ I, então f é uma função
côncava para baixo no intervalo I.
Aula 21
Cálculo I
8
Justificativa
Aula 21
Cálculo I
9
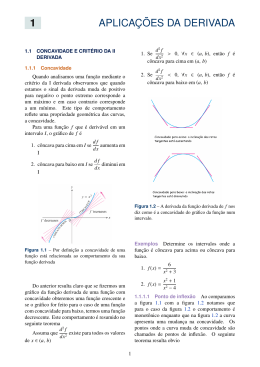
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
.
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
10
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
.
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
11
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
.
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
12
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
.
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
13
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
.
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
14
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
.
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
15
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
.
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
16
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
Sinal da
derivada
segunda
.
0
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
17
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
Sinal da
derivada
segunda
.
0
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
18
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
Sinal da
derivada
segunda
.
0
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
19
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
Sinal da
derivada
segunda
.
0
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
20
Exemplo
Seja y = f (x) = x 3 − 9 x.
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Temos que f 0 (x) = 3 x 2 − 9 e, portanto, f 00 (x) = 6 x. Vamos estudar
o sinal da derivada segunda:
Sinal da
derivada
segunda
.
0
Assim, f é côncava para baixo no intervalo (−∞, 0) e f é côncava para cima
no intervalo (0, +∞). Conseqüentemente, p = 0 é o único ponto de inflexão
de f .
Aula 21
Cálculo I
21
Estudo da concavidade da função y = f (x) = x 3 − 9 x
p = 0 é o único ponto de inflexão de f .
Aula 21
Cálculo I
22
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
23
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
24
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
25
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
26
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
27
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
28
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
29
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Sinal da
derivada
segunda
.
{2
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
30
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Sinal da
derivada
segunda
.
{2
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
31
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Sinal da
derivada
segunda
.
{2
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
32
Exercício
Seja y = f (x) = x ex .
Determine os intervalos onde f é côncava para cima, os intervalos
onde f é côncava para baixo e os pontos de inflexão de f
(os pontos no domínio de f onde existe mudança de concavidade).
Solução. Já vimos que f 0 (x) = (x + 1) ex . Logo, f 00 (x) = ex + (x + 1) ex =
(x + 2) ex . Vamos estudar o sinal da derivada segunda:
Sinal da
derivada
segunda
.
{2
Assim, f é côncava para baixo no intervalo (−∞, −2) e f é côncava para
cima no intervalo (−2, +∞). Conseqüentemente, p = −2 é o único ponto de
inflexão de f .
Aula 21
Cálculo I
33
Classificando pontos críticos usando a
derivada segunda
Aula 21
Cálculo I
34
O teste da derivada segunda
Teorema
Sejam f : D → C, A um subconjunto do domínio D e p é um ponto
crítico de f no interior de A. Suponha que f , f 0 e f 00 sejam contínuas.
(1) Se f 00 (p) > 0 , então p é ponto de mínimo local de f em A.
(2) Se f 00 (p) < 0 , então p é ponto de máximo local de f em A.
Aula 21
Cálculo I
35
O teste da derivada segunda
Teorema
Sejam f : D → C, A um subconjunto do domínio D e p é um ponto
crítico de f no interior de A. Suponha que f , f 0 e f 00 sejam contínuas.
(1) Se f 00 (p) > 0 , então p é ponto de mínimo local de f em A.
(2) Se f 00 (p) < 0 , então p é ponto de máximo local de f em A.
Aula 21
Cálculo I
36
O teste da derivada segunda
Teorema
Sejam f : D → C, A um subconjunto do domínio D e p é um ponto
crítico de f no interior de A. Suponha que f , f 0 e f 00 sejam contínuas.
(1) Se f 00 (p) > 0 , então p é ponto de mínimo local de f em A.
(2) Se f 00 (p) < 0 , então p é ponto de máximo local de f em A.
Aula 21
Cálculo I
37
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
38
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
39
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
40
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
41
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
42
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
43
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
44
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
45
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
46
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
47
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
48
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
49
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
50
Exemplo
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x 3 − 9 x.
0
Solução. Temos que
3 x 2 − 9 = 3 (x 2 − 3) e, portanto, f 00 (x) = 6 x.
√ f (x) = √
Vimos que p = − 3 e q = + 3 são os únicos pontos críticos de f . Como
√
√
f 00 (p) = f 00 (− 3) = −6 3 < 0,
√
segue-se que p = − 3 é ponto de máximo local de f em R. Do mesmo
modo, como
√
√
f 00 (q) = f 00 (+ 3) = +6 3 > 0,
√
segue-se que q = + 3 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
51
Exemplo: y = f (x) = x 3 − 9 x, A = R
√
extremos locais em A: p = − 3 é ponto de máximo local
A função f possui apenas √
e q = + 3 é ponto de mínimo local de f em A.
Aula 21
Cálculo I
52
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
53
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
54
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
55
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
56
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
57
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
58
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
59
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
60
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
61
Exercício
Use o teste da derivada segunda para classificar os pontos críticos
de y = f (x) = x ex .
Solução. Já vimos que p = −1 é o único ponto crítico de f . Também já vimos
que f 00 (x) = (x + 2) ex . Como
f 00 (p) = f 00 (−1) = (−1 + 2) e−1 = e−1 > 0,
segue-se que p = −1 é ponto de mínimo local de f em R.
Aula 21
Cálculo I
62
Cuidado!
Se f 00 (p) = 0, nada podemos afirmar sobre o ponto p:
ele pode ser um ponto de mínimo local, um ponto de máximo local
ou um ponto de sela.
y
y
y
f
0
h
x
0
0
x
x
g
f (x) = +x 4
Aula 21
g(x) = −x 4
h(x) = +x 3
Cálculo I
63
Como fazer um bom esboço do gráfico
de uma função?
Aula 21
Cálculo I
64
Exercício
Tente fazer um esboço do gráfico da função
y = f (x) = x ex .
Faça cada gráfico em um sistema de eixos coordenados diferente.
Use o que quiser, inclusive a sua calculadora!
Aula 21
Cálculo I
65
Cuidado: usar tabelas pode não ser suficiente!
Aula 21
Cálculo I
66
Cuidado: usar tabelas pode não ser suficiente!
Aula 21
Cálculo I
67
Cuidado: usar tabelas pode não ser suficiente!
Aula 21
Cálculo I
68