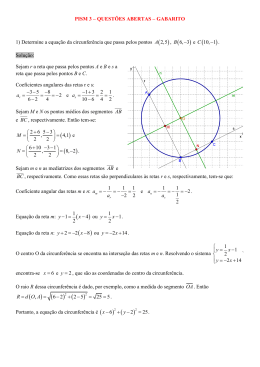
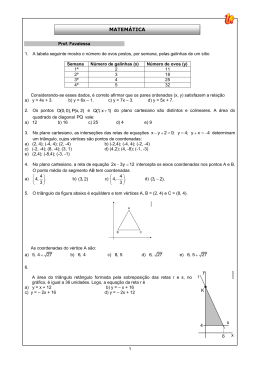
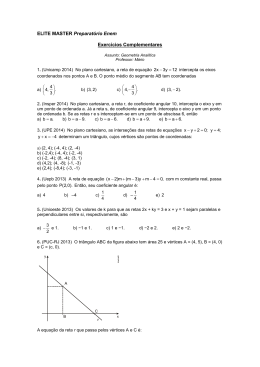
Revisão 01 Geometria Analítica Retas Prof. PH [email protected] Formas da equação da reta 1) Forma Reduzida y Coef. Angular = m Coef. Linear = n r n y = mx + n Coef. Angular: m = tg x 2) Forma Geral ax + by + c = 0 Coef. Angular = -a/b Coef. Linear = -c/b Ex) Obter a equação geral da reta que passa pelos pontos A(1,1) e B(-2,5). Solução: 1 -2 x 1 1 5 y 1 =0 5 - 2y + x – y – 5x + 2 = 0 – 4x – 3y + 7 = 0 3) Forma Segmentária x p y r q p x + y =1 q 4) Forma Paramétrica x = f(t) y = g(t) Ex) Obter a equação geral da reta dada por Solução: Isolando t na segunda equação: y – 5 = t Substituindo t na primeira equação: x = 2t - 1 x = 2( y – 5 ) - 1 x = 2y – 10 - 1 x = 2y – 11 x – 2y + 11 = 0 x = 2t - 1 y=t+5 5) Equação do feixe y – yo = m(x – xo) m = Coef. Angular P(xo, yo ): ponto dado Ex) Obter a equação geral da reta abaixo: Solução: m = tg150o = y P(3,2) 3 3 y – yo = m(x – xo) 2 y - 2 = 150o 3 x 3 (x – 3) 3 3y - 6 = 3 x + 3 3 3 x + 3y - 3 3- 6 = 0 Anote aí: 1) Retas paralelas têm coeficientes angulares iguais Retas perpendiculares têm coeficientes angulares 2) inversos e opostos Reta horizontal tem coeficiente angular igual a zero. 3) Sempre do tipo y = k Reta vertical não tem coeficiente angular. 4) Sempre do tipo x = k m m 5) Ângulo agudo entre duas retas: tg 1 m .m r s r Quando uma delas for vertical: tg 1 mr s Anote aí: a.xP b. yP c 6) Distância entre ponto e reta: d 7) Distância entre duas retas paralelas: P ,r a 2 b2 Escolher um ponto de uma reta e calcular a sua distância até a outra reta, ou Usar a fórmula: dr ,s c1 c2 a 2 b2 da reta que passa por 8) Coef.yangular y m A B x A xB A(xA , yA ) e B(xB , yB) FIM !!!
Download