CENTRO FEDERAL DE EDUCAÇÃO
TECNOLÓGICA DE MINAS GERAIS
Diretoria de Pesquisa e Pós-Graduação
Programa de Mestrado em Modelagem
Matemática e Computacional
Roteamento em Redes Interligadas
modeladas por Grafos Circulantes e
Gaussianos
Dissertação de Mestrado, submetida ao Programa
de Pós-Graduação em Modelagem Matemática e
Computacional, como parte dos requisitos exigidos
para a obtenção do título de Mestre em Modelagem Matemática e Computacional.
Aluno: Luiz Otávio Rodrigues Alves Sereno
Orientador: Prof. Dr. Rodrigo Tomás Nogueira Cardoso
Co-Orientadora: Prof.a Dra. Sandra Mara Alves Jorge
Belo Horizonte - MG
Fevereiro de 2012
Agradecimentos
A Deus pelo dom da vida e pela oportunidade de poder estudar e buscar a realização
dos meus sonhos!
Aos meus pais Luiz Fernando e Sueli por me ensinarem o caminho em que devo
andar e que ao continuar crescendo não me desvie dele. E a minha irmã Ana Claudia
por me ajudar a compreender melhor o signicado do termo família.
Aos meus orientadores Rodrigo e Sandra pela conança, apoio, ensinamentos,
por todo empenho, sabedoria, compreensão e, principalmente, exigência. Agradeço
também às professoras Dra. Ana Cristina Vieira e Dra. Elizabeth Fialho Wanner
por aceitarem o convite de compor a banca e pelas sugestões ao trabalho.
A minha namorada Sabrina pelo apoio de sempre e pelo incentivo incessante,
mesmo nos momentos de maior diculdade.
A minha prima Shirley e a seu marido Guilhereme por terem me recebido em
Belo Horizonte assim que cheguei e por terem me ajudado sempre que precisei. Ao
meu primo Antônio Carlos, sua esposa Aleice e toda sua família pela receptividade
e ajuda nas diculdades que encontrei na capital mineira.
Aos amigos que z no CEFET-MG nestes dois anos, pelas horas de estudos e por
tornarem bem melhores meus dias em BH. Agradeço em especial a Lillia, Jahína,
Gustavo, Flaviana, Carla, Jeanderson, Kay, Mayra, Moisés, Saulo, José Maurício,
Nilmar e a todos que compartilharam momentos bons e ruins no curso.
A CAPES pelo auxílio nanceiro durante a caminhada.
Finalmente, agradeço a todas as pessoas que, direta ou indiretamente, contribuíram para a execução dessa Dissertação de Mestrado.
ii
Resumo
O objetivo principal deste trabalho é estudar o roteamento de redes interligadas
modeladas por diferentes topologias de grafos, pretendendo, por exemplo, tornar
mais eciente o cálculo das distâncias mínimas.
circulantes e os gaussianos.
Dois tipos foram escolhidos:
os
Com base na tese de Martínez (2007), é apresentado
um estudo teórico das estruturas matemáticas destes grafos, que são importantes
no desenvolvimento das ferramentas consideradas. Algoritmos ecientes são propostos para calcular o caminho mais curto entre dois vértices, e suas implementações
computacionais permitirão uma visualização gráca das redes e seus roteamentos
ótimos.
Além disso, a partir do artigo de Yanga (2009), estuda-se a construção
de árvores geradoras independentes para uma classe especial de grafos circulantes,
innalizando com uma extensão para grafos gaussianos em geral.
PALAVRAS-CHAVE: Grafo Gaussiano; Grafo Circulante; Redes interligadas;
Roteamento.
iii
Abstract
The main objective of this work is to study the routing of interconnected networks modelled by dierent graph topologies, intending, for example, become more
ecient the computation of minimal distances. Two types were chosen: the circulants and the gaussians. Based on the thesis of Martínez (2007), it is presented a
theoretical study of the mathematical structures of these graphs, which belong together in the development of the considered tools. Ecient algorithms are proposed
for calculate the shortest path between two vertices, and their computational implementations will permit a graphic visualization of the networks and their optimal
routings. Furthermore, from the Yanga's (2009) article, it studies the construction
of independent spanning trees for a special type of circulants graphs, completing
with an extension for gaussian graphs in general.
KEY-WORDS: Gaussian Network; Circulant Graph; interconnected networks;
Routing.
iv
Sumário
1 Anel dos Inteiros Gaussianos
2
1.1
Fatos Básicos
1.2
Anéis Quocientes de Inteiros Gaussianos
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . .
2 Grafos Circulantes e Gaussianos
2
8
12
2.1
Fatos básicos sobre Grafos . . . . . . . . . . . . . . . . . . . . . . . .
12
2.2
Grafos Circulantes
17
2.2.1
2.3
Algoritmo de Euclides Estendido
. . . . . . . . . . . . . . . .
18
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
Diâmetro e Distância média de um grafo Gaussiano . . . . . .
26
Grafos Gaussianos
2.3.1
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 O problema do caminho mais curto
3.1
3.2
Algoritmo de Dijkstra
Roteamento em Grafos Circulantes
3.2.1
3.3
. . . . . . . . . . . . . . . . . . .
Programa para Roteamento em Grafos Circulantes
38
38
. . . . . . . . . . . . . . . . . . .
41
Programa para Roteamento em Grafos Gaussianos . . . . . . .
43
4 O problema das árvores geradoras independentes
4.1
36
. . . . . .
Roteamento em Grafos Gaussianos
3.3.1
36
. . . . . . . . . . . . . . . . . . . . . . . . . .
46
4.2
Árvores Geradoras Independentes (IST)
. . . . . . . . . . . . . . . .
m
Construindo IST's em C(cd , d) com d > 2 . . . . . . . . . . . . . . .
56
4.3
Prova da vericidade do algoritmo
. . . . . . . . . . . . . . . . . . . .
60
4.4
IST's em grafos gaussianos . . . . . . . . . . . . . . . . . . . . . . . .
64
5 Conclusão e Trabalhos Futuros
46
67
5.1
Conclusão
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
5.2
Trabalhos Futuros . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
v
Lista de Tabelas
2.1
Distribuição de pesos no caso ímpar . . . . . . . . . . . . . . . . . . .
2.2
Distribuição de pesos no caso par com
2.3
Distribuição de pesos no caso par com
vi
a<b
a=b
30
. . . . . . . . . . . . . .
33
. . . . . . . . . . . . . .
33
Lista de Figuras
2.1
Exemplo de grafo com 7 vértices . . . . . . . . . . . . . . . . . . . . .
13
2.2
Modelagem de redes através de grafos . . . . . . . . . . . . . . . . . .
13
2.3
Exemplo de grafo de grau 3
14
2.4
Exemplo de dois grafos isomorfos
2.5
Grafo conexo
2.6
Grafo
2.7
Grafos isomorfos
2.8
Pontos cuja norma é igual à
2.9
Translações das Regiões
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
15
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
G = (D, E)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
|α| . . . . . .
Q, T, −T, iT e −iT
. . . . . . . . . . . . . . .
28
. . . . . . . . . . . . . .
30
2.10 Distribuição de pesos no grafo gaussiano gerado por 2 + 7i . . . . . .
2.11 Translações da Região
Qt−1 ,
Segmentos e Triângulo da Prova . . . . .
3.1
Grafo Circulante com 18 vértices e saltos 3 e 5 . . . . . . . . . . . . .
3.2
Menor caminho entre os vértices 1 e 12 do Grafo Circulante
|g|
e
|h|
C18 (3, 5)
3.3
Gráco das funções
3.4
Grafo Gaussiano gerado por
. . . . . . . . . . . . . . . . . . . . . . .
3.5
Grafo Gaussiano gerado por
3.6
Menor caminho entre os vértices 5+3i e 7+0i do grafo gaussiano
3.7
Menor caminho entre os vértices 5+3i e 7+0i do grafo gaussiano
5 + 8i
5 + 8i
. . . . . . . . . . . . . . . . . . .
na topologia losangular
31
32
39
39
40
43
. . . . . .
44
G3+5i
G3+5i
44
na topologia em L . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
4.1
Exemplo de caminhos disjuntos
46
4.2
Árvores Geradoras
4.3
C(18, 3) . . . . . . . . .
Grafo circulante recursivo C(18, 3)
. . . . . . . . .
m−1
Vértices adjacentes a j no grafo C(cd
, d) . . . .
Árvores Geradoras Independentes no grafo C(16, 4)
−
Árvore T0 do grafo C(18, 3) . . . . . . . . . . . . .
+
Árvore T0 do grafo C(18, 3) . . . . . . . . . . . . .
−
Árvore T1 do grafo C(18, 3) . . . . . . . . . . . . .
+
Árvore T1 do grafo C(18, 3) . . . . . . . . . . . . .
−
Árvore T2 do grafo C(18, 3) . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
. . . . . . . . . .
48
. . . . . . . . . .
49
. . . . . . . . . .
50
. . . . . . . . . .
52
. . . . . . . . . .
58
. . . . . . . . . .
58
. . . . . . . . . .
59
. . . . . . . . . .
59
. . . . . . . . . .
59
4.12 Árvore 2 gerada pelo programa
. . . . . . . . . . . . . . . . . . . . .
65
4.13 Árvore 3 gerada pelo programa
. . . . . . . . . . . . . . . . . . . . .
65
4.14 Árvore 4 gerada pelo programa
. . . . . . . . . . . . . . . . . . . . .
65
4.15 Árvore Geradora 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
4.16 Árvore Geradora 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
4.17 Árvore Geradora 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
4.4
4.5
4.6
4.7
4.8
4.9
4.10
4.11
Grafo circulante recursivo
vii
Introdução
Em todos os sistemas que fazem uso de redes interligadas, uma comunicação eciente entre os nós dessa rede torna-se necessária. A tarefa de enviar um conjunto
de dados de um ponto a outro pede uma busca pelo melhor caminho possível, ou
seja, aquele que dará menor custo. A esse processo chamamos de roteamento, que
iremos trabalhar ao longo deste trabalho em alguns tipos de redes. Numa rede de
computadores do tipo LAN (Local Area Network), por exemplo, a transmissão de
dados entre pontos da mesma deve se realizar de forma a percorrer o menor caminho
até chegar ao destino desejado.
Estas redes podem ser modeladas através de grafos, importantes objetos matemáticos que permitem também a modelagem de diversos outros problemas reais.
Entretanto, a busca de soluções para grafos em geral com baixo custo computacional
se torna complicada. Existem classes especícas de grafos que tratam problemas de
forma mais restrita, o que permite reduzir esse custo ao trabalhar com estruturas
mais conhecidas.
Neste trabalho, estudamos principalmente duas dessas classes:
os grafos circulantes, muito usados há algumas décadas, e grafos gaussianos, que
aparecem na literatura de forma mais recente e que, sob algumas condições, são
isomorfos aos primeiros.
A busca do menor caminho entre os vértices de um grafo, passando pelas arestas
pertencentes ao mesmo, é um dos principais problemas da Teoria de Grafos. Tratase de um dos mais conhecidos e antigos problemas na pesquisa operacional e sua
solução foi sugerida até mesmo em lendas mitológicas da Grécia Antiga. Ele aparece,
por exemplo, na robótica, onde são necessários bons algoritmos para navegação, e
está associado a um enorme número de outros problemas na área de roteamento,
manufatura, uxos em redes etc.
Ao longo dos anos, muitos algoritmos surgiram
para resolução desse problema. Existem na literatura alguns resultados e algoritmos,
como o proposto por Dijkstra em 1959, que pode ser utilizado em praticamente todos
os tipos de grafos, e o de Ford-Moore-Bellman, uma generalização do primeiro.
Apesar disso, o custo computacional desses algoritmos é elevado para problemas
com um número grande de vértices. Neste trabalho, propomos formas alternativas
de resolvê-lo, restritas às classes dos grafos circulantes e gaussianos com baixo custo
computacional.
A escolha da topologia é feita de forma que o grafo correspondente tenha bons
parâmetros, propriedades que caracterizam um grafo.
A inserção de mais arestas
garante, por exemplo, maior conectividade e, consequentemente, robustez. Entretanto, deve-se evitar um aumento do diâmetro do grafo, ou seja, a maior distância possível existente na combinação dois-a-dois de vértices.
Grafos circulantes e
grafos gaussianos são classes de grafos dotadas com topologias interessantes para
viii
0.0
1
a resolução do problema citado anteriormente. Os primeiros possuem alto grau de
conectividade e diâmetros aceitáveis, além de possuírem simetria. Já os últimos têm
a vantagem de possuírem como rótulos os seus vértices, isto é, o nome atribuído a
eles, os inteiros gaussianos, que são um subconjunto dos números complexos com a
parte real e a parte imaginária pertencentes aos inteiros, o que lhes dá uma forma
bastante conveniente de rotulação ao dispor os vértices no plano cartesiano.
Este trabalho apoia-se no estudo mais detalhado de Martínez (2007), tese de
doutorado com o título
Codes and Graphs over Complex Integer Rings,
e no artigo
Martínez (2008) da mesma autora, apresentando, inclusive, provas que não foram
explicitadas ou provas alternativas para alguns teoremas. As pesquisas que envolvem
os grafos Gaussianos apresentam-se de forma relativamente recente. Podemos citar,
On Shortest Disjoint Paths and Hamiltonian Cycles in Some
Interconnection Networks de Hussein (2011), que utiliza tais grafos em problemas
por exemplo, a tese
relacionados a encontrar caminhos com vértices disjuntos em certas classes de redes
interligadas.
Por último, trabalhamos com o problema da busca de árvores geradoras independentes, fazendo uma releitura do artigo de Yang (2009), que trata do caso de
grafos circulantes, em que se propõe um algoritmo para construção de árvores geradoras independentes para uma subclasse especíca desses grafos.
Estas árvores
são utilizadas, por exemplo, em transmissão e distribuição de mensagens em redes
interligadas. Finalizando o trabalho, é proposto um estudo sobre árvores geradoras
em grafos Gaussianos. Este mesmo problema também é tratado de forma mais recente pelo artigo Yang (2010), no caso particular dos grafos circulantes recursivos,
em que os parâmetros valem
d=2
e
c = 1.
Através do software MATLAB, foram desenvolvidos algoritmos que tratam do
roteamento de grafos circulantes e gaussianos, além de algoritmos que fazem a transição entre diferentes topologias de grafos gaussianos.
Também foram propostos
algoritmos para a busca de árvores geradoras independentes (IST's) em grafos circulantes recursivos e grafos gaussianos.
Capítulo 1
Anel dos Inteiros Gaussianos
O estudo de roteamento em redes interligadas, objetivo principal deste trabalho,
pode ser feito de maneira mais eciente através do uso de algumas classes especícas de grafos, nas quais baseiam-se no estudo do Anel dos Inteiros Gaussianos. Para
melhor compreensão desse anel, apresentamos neste capítulo algumas denições básicas do contexto de Álgebra Abstrata, juntamente com alguns resultados, que podem
ser encontrados em Gilbert (2004), Gonçalves (1979) e Hungerford (1997). Veremos,
por exemplo, que o anel dos Inteiros Gaussianos é um domínio euclidiano. Esta estrutura algébrica será utilizada na construção dos grafos Gaussianos, que veremos
mais tarde.
1.1
Fatos Básicos
Denição 1.1 Um grupo (G, ∗) é um conjunto junto com uma operação binária ∗
que satisfaz os seguintes axiomas.
(i) A operação ∗ é associativa; isto é, (a ∗ b) ∗ c = a ∗ (b ∗ c) para todos a, b, c ∈ G .
(ii) Existe um elemento neutro e ∈ G tal que e ∗ a = a ∗ e = a, para todo a ∈ G .
(iii) Cada elemento a ∈ G tem um elemento inverso a−1 ∈ G tal que a−1 ∗ a =
a ∗ a−1 = e.
Além disso, se a ∗ b = b ∗ a, ∀a, b ∈ G , dizemos que G é um grupo abeliano.
Pelo contexto, denotaremos
a∗b
por
ab.
Denição 1.2 Se G é um grupo e H é um subconjunto não-vazio de G , então H é
chamado subgrupo de G , denotado por H ≤ G , se ocorrerem as seguintes condições:
(i) ab ∈ H para todos a, b ∈ H .
(ii) a−1 ∈ H para todo a ∈ H .
Exemplo 1.1 O conjunto Z[i] = {a + bi|a, b ∈ Z} ⊂ C com a operação usual de
soma é um grupo.
2
1.1
Anel dos Inteiros Gaussianos
3
a ∈ G , dizemos que hai = {an |n ∈ Z} é o subgrupo cíclico
2
n
gerado por a. Note que se G é nito, então hai = {a, a , ..., a } para o n ∈ Z tal
n
que a = e. De modo mais geral, dado um subconjunto não-vazio S ⊆ G , denimos
o conjunto de todos os possíveis produtos, em qualquer ordem, dos elementos de S
e de seus inversos como sendo o subgrupo de G gerado por S , cuja notação é dada
por hSi.
Seja G um grupo e H ≤ G . Então dizemos que, para cada x ∈ G , Hx = {hx :
h ∈ H} é a classe lateral à direita de H em G .
Se criarmos a relação de equivalência em G tal que
Dado
G
um grupo e
x ∼ y ⇔ xy −1 ∈ H,
tem-se que:
x ∼ y ⇔ xy −1 = h ∈ H ⇔ x = hy ⇔ x ∈ Hy
Logo,
Hx
x.
f : H → Hx, que leva h em hx, vemos que f é uma bijeção.
classes laterais de H em G têm a mesma cardinalidade de H .
é a classe de equivalência de
Tomando a função
Assim, todas as
O conjunto das classes de equivalência é denotado por:
G/H = {Hx|x ∈ G}
Note que se G/H é nito, digamos, G/H = {Hx1 , Hx2 , . . . , Hxn }, então G =
Hx1 ∪ Hx2 ∪ . . . ∪ Hxn e Hxi ∩ Hxj = ∅, se i 6= j .
Com isso e denotando por |X| a cardinalidade de um conjunto X nito, podemos
provar o seguinte resultado:
Teorema 1.1 (Teorema de Lagrange): Se G é um grupo nito e H é um subgrupo
|G|
.
de G , então |H| divide |G| e |G/H| = |H|
Dem.: Considerando a relação de equivalência à direita em G , obtemos, como
vimos, uma partição de G em n classes de equivalência. Como cada uma dessas
|G|
classes possui |H| elementos, então |G| = n · |H|, ou seja, n = |H|
. Sendo n classes,
então |G/H| = n.
Denição 1.3 Dizemos que (A, +, ·) é um anel com as operações · e + se satisfaz
as propriedades:
(i) O conjunto A com a operação + forma um grupo abeliano.
(ii) A operação · é fechada em A.
(iii) Associatividade para multiplicação, isto é, (a · b) · c = a · (b · c), para todos
a, b, c ∈ A.
(iv) Distributividade da soma em relação à multiplicação, isto é, (a + b) · c =
a · c + b · c , para todos a, b, c ∈ A.
1.1
Anel dos Inteiros Gaussianos
4
Se além dessas propriedades, também valer a · b = b · a, para todos a, b ∈ A
(Comutatividade da multiplicação), então (A, +, ·) será um anel comutativo. Se
existir 1 ∈ A tal que 1 · a = a para qualquer elemento a ∈ A, então (A, +, ·) será
um anel com unidade.
Denição 1.4 Sejam G e H dois grupos.
(i) Um homomorsmo f : G → H é uma função tal que f (ab) = f (a)f (b) para
todos a, b ∈ G .
(ii) Um isomorsmo f : G → H é um homomorsmo bijetor.
Quando existe um isomorsmo entre os grupos G e H , dizemos que G e H são
isomorfos e denotaremos por G ∼
= H.
Analogamente, podemos introduzir os conceitos de homomorsmo e isomorsmo
entre anéis.
Denição 1.5 Sejam dois anéis R e S . Dizemos que f : R → S é um homomor-
smo de anéis, se f (a + b) = f (a) + f (b) e f (ab) = f (a)f (b). Além disso, R e S
são isomorfos, com notação R ∼
= S , se existir uma função f : R → S que seja um
isomorsmo, isto é, um homomorsmo bijetor.
Observe que, de acordo com a denição, se
f (0R ) = 0S ,
f
é um homomorsmo de anéis, então
ou seja, o elemento neutro da soma do primeiro anel é sempre levado
no elemento neutro do segundo.
Im(f ) de um
isomorsmo f : R → S da seguinte forma: Im(f ) = {f (x) ∈ S, x ∈ R}. Além disso,
denimos o conjunto N uc(f ) = {x ∈ R, f (x) = 0}, o chamado núcleo de f .
Assim como no contexto de funções reais, denimos a imagem
Denição 1.6 Dizemos que um anel é domínio de integridade se ele for comutativo,
com unidade e que nele a multiplicação de quaisquer dois elementos não-nulos é nãonula, ou seja, se a, b ∈ A são não-nulos, então a · b 6= 0, onde 0 é o elemento neutro
da adição.
Exemplo 1.2
√ Seja m ∈ Z − {0, 1} um número livre de quadrados. Considere A =
Dm = {a + b m/a, b ∈ Z}. Então:
(i) A é um domínio de integridade com Z ⊆ A ⊆ C. √
(ii) Tomando m = −1, temos o domínio D−1 = {a + b −1/a, b ∈ Z} = {a +
bi/a, b ∈ Z} = Z[i], chamado o Anel dos Inteiros de Gaussianos.
Denição 1.7 Seja (A, +, ·) um anel. Então ∅ 6= I ⊆ A será um ideal de A se
0 ∈ I , a + (−b) ∈ I , para todos a, b ∈ I e se dado x ∈ I , então para qualquer
elemento a ∈ A valer x · a ∈ I e a · x ∈ I .
1.1
Anel dos Inteiros Gaussianos
5
a ∈ A, I = (a) = {x · a|x ∈ A}, se o anel A for comutativo, I é
um ideal de A gerado por um único elemento. I é dito um ideal principal.
Dados A um anel e I um ideal de A, denimos, para cada a ∈ A, a classe de I em
A, a+I = {a+x|x ∈ I}. Note que a−b ∈ I se, e somente, se a+I = b+I . Denotamos
por A/I = {a+I|a ∈ A}, o conjunto de todas as classes laterais. Verica-se que A/I
herda uma estrutura de anel mediante as operações (a + I) + (a0 + I) = (a + a0 ) + I
e (a + I) · (a0 + I) = (a · a0 ) + I de sorte que a aplicação denida naturalmente por
h : A → B tal que h(a) = a + I seja um homomorsmo.
Note que dado
Exemplo 1.3 Se α ∈ Z[i], então (α) e (αα) são ideais de Z[i] e (ᾱα) é ideal de
(α). Logo,
(α)
(αα)
é ideal de
Z[i]
(αα)
.
Teorema 1.2 (Primeiro Teorema do Isomorsmo) Seja ϕ : A → S um hoA
∼
momorsmo de anéis. Então N uc(ϕ)
= Im(ϕ).
A
Dem.: Dena φ : N uc(ϕ) → Im(ϕ), dada por φ(r + N uc(ϕ)) = ϕ(r).
A função φ está bem denida e é um homomorsmo. De fato, como ϕ é homomorsmo, então φ também é homomorsmo e r + N uc(ϕ) = r0 + N uc(ϕ) implica r − r0 ∈ N uc(ϕ), ou seja, ϕ(r − r0 ) = 0. Sendo ϕ um homomorsmo vale
ϕ(r) − ϕ(r0 ) = 0, isto é, ϕ(r) = ϕ(r0 ).
Provemos que φ é bijetora. Para isso, note que se r + N uc(ϕ) ∈ N uc(φ), então
φ(r + N uc(ϕ)) = 0. Assim, ϕ(r) = 0 e r ∈ N uc(ϕ). Logo, r + N uc(ϕ) = N uc(ϕ) e
N uc(φ) = {0 + N uc(ϕ)}. Portanto, φ é injetora e, por denição, φ é sobrejetora.
A
∼
Assim, podemos concluir que φ é um isomorsmo, o que nos dá N uc(ϕ)
= Im(ϕ).
Teorema 1.3 (Terceiro Teorema do Isomorsmo) Sejam I, J ideais do anel
∼ A.
é ideal de AJ e A/J
I/J = I
Dem.: Primeiramente, note que:
i) JI 6= ∅, pois 0 + J ∈ JI .
ii) a + J, a0 + J ∈ JI implica (a + J) − (a0 + J) = (a − a0 ) + J ∈ JI .
iii) Se a+J ∈ JI e r+J ∈ AJ , então (a+J)(r+J) = ar+aJ +Jr+J = ar+J ∈ JI ,
pois I, J são ideais de A.
Dos itens anteriores, concluímos que JI é ideal de AJ .
Agora dena ϕ : AJ → AI , sendo ϕ(r + J) = r + I . ϕ está bem denida e é um
homomorsmo. Além disso, N uc(ϕ) = JI .
Se r + J ∈ N uc(ϕ), então ϕ(r + J) = 0 + I . Daí, r + I = 0 + I e, dessa forma,
r ∈ I . Portanto, r+J ∈ JI . Se a+J ∈ JI , então a ∈ I ⊆ A e ϕ(a+J) = a+I = 0+I .
Logo, a + J ∈ N uc(ϕ).
ϕ é sobrejetora. De fato, se r + I ∈ AI , então r + J ∈ A
e ϕ(r + J) = r + I .
J
A/J
∼
Pelo Primeiro Teorema do Isomorsmos, temos: N uc(ϕ) = Im(ϕ) = AI . Portanto,
A/J ∼ A
.
I/J = I
A, com J ⊆ I . Então:
I
J
1.1
Anel dos Inteiros Gaussianos
Exemplo 1.4 Se α ∈ Z[i], temos que
6
é ideal de (Z[i]
e, no contexto de gruᾱα)
é subgrupo do grupo (Z[i]
, que é nito (veja Teorema 1.6). Portanto, dos
pos, ((α)
ᾱα)
ᾱα)
Teoremas 1.1 e 1.3, temos:
Z[i]
(αα)
(α)
(αα)
∼
=
Z[i]
(α)
e
(α)
(ᾱα)
Z[i]
| (αα) |
(α)
| (αα) |
|.
= | Z[i]
(α)
A seguir, recordemos o conceito de um importante domínio na álgebra abstrata:
os domínios euclidianos.
Denição 1.8 Seja A um anel. Dizemos que A é um domínio euclidiano se A é
um domínio de integridade e se existe uma função: N : A − {0} → Z tal que:
(i) N (a) ≥ 0, para todo a ∈ A − {0}.
(ii) N (a) ≤ N (ab), para todos a, b ∈ A − {0}.
(iii) Dados quaisquer a, b ∈ A, b 6= 0, existem q, r ∈ A tais que a = bq + r e
r = 0 ou N (r) < N (b).
Dado um domínio euclidiano, um fato importante é que faz sentido denirmos
máximo divisor comum entre quaisquer dois de seus elementos.
x, y ∈ A,
y = cx.
Consideremos, para
existe
c∈A
tal que
a notação
x|y
(lê-se
x
divide
y)
para indicar que
Denição 1.9 Seja A um domínio euclidiano e a, b ∈ A (ambos não-nulos). Um
máximo divisor comum de a e b é um elemento d tal que:
(i) d|a e d|b
(ii) Se c|a e c|b, então N (c) ≤ N (d).
Se d é um máximo divisor comum de a e b, então denotaremos d por d =
mdc(a, b).
Exemplo 1.5 Os inteiros Z, com a norma usual de módulo constituem um domínio
euclidiano. Além disso, o Anel dos Inteiros Gaussianos Z[i] = {a+bi/a, b ∈ Z} é um
domínio euclidiano com a função N : Z[i] → N tal que N (a + bi) = a2 + b2 . Note que
N (α) > 0, ∀α ∈ Z[i] − {0}. Além disso, para quaisquer α, β ∈ Z[i] tem-se N (α) ≤
N (α)N (β) = N (αβ), onde a desigualdade deve-se ao fato de N (β) ≥ 1 seja qual
for β ∈ Z[i]. Sejam α, β ∈ Z[i], com β 6= 0. Então αβ = x + iy ∈ C. Existem
e, f ∈ Z tais que |x − e| ≤ 12 e |y − f | ≤ 21 . Dena δ = e + if ∈ Z[i] e considere
ρ = α − βδ = β( αβ − δ). Assim, N (ρ) = N (β)N ( αβ − δ) = N (β)N (x + iy − e − if ) =
N (β)N (x − e + i(y − f )) = N (β)[(x − e)2 + (y − f )2 ] ≤ N (β)( 41 + 14 ) = N 2(β) < N (β).
Logo, α = βδ + ρ, onde N (ρ) < N (β).
Não é difícil ver que o máximo divisor comum existirá para quaisquer dois elementos de
A
pertencentes a um domínio euclidiano. Um outro fato necessário para
1.1
Anel dos Inteiros Gaussianos
7
o nosso trabalho é o teorema seguinte. Porém, antes de enunciá-lo e prová-lo, lembremos que dado
tal que
uv = 1A .
unidade, tal que
A
um anel, um elemento
Além disso, dizemos que
u ∈ A é unidade em A, se existir v ∈ A
a, b ∈ A são associados se existe u ∈ A,
a = bu.
Teorema 1.4 Seja A um domínio euclidiano e a, b ∈ A (ambos não-nulos). Se
d = mdc(a, b), então
(i) Todo associado de d é também um máximo divisor comum de a e b.
(ii) Existem x0 , y0 ∈ A tais que d = ax0 + by0 .
(iii) Se existirem x0 , y0 ∈ A tais que 1A = ax0 + by0 , então mdc(a, b) = 1A , isto
é, a e b são relativamente primos.
Dem.:
(i) Seja d1 um elemento associado de d. Então d = d1 u, onde u é unidade de A.
Como d|a e d|b, temos a = dt e b = dt1 , ou seja, a = d1 ut e b = d1 ut1 . Portanto,
d1 |a e d1 |b. Agora se c|a e c|b, então N (c) ≤ N (d) = N (d1 u) = N (d1 ), pois u é
unidade de A. Assim, d1 = mdc(a, b).
(ii) Seja S = {N (w)|0 6= w ∈ Aew = as + bt, para algum s, t ∈ A} ⊂ N. Como
a = a1A + b0A ou b = a0A + b1A é não-nulo, segue que S 6= ∅. Pelo princípio
da boa ordenação, S tem um menor elemento, ou seja, existem d1 , x1 , y1 ∈ A tais
que d1 = ax1 + by1 e que para todo w ∈ A tal que w = as + bt, s, t ∈ A, tem-se
N (d1 ) ≤ N (w). É verdade que d1 = mdc(a, b). De fato, existem q, r ∈ A tais que
a = d1 q+r, onde r = 0 ou N (r) < N (d1 ) implica que r = a−d1 q = a−(ax1 +by1 )q =
a(1 − qx1 ) + b(−y1 q).
Assim, se r 6= 0, então r ∈ S e, assim, N (d1 ) ≤ N (r), o que é absurdo. Logo,
r = 0 e a = d1 q , isto é, d1 |a. Analogamente, d1 |b. Agora se c|a e c|b, então a = ct
e b = ck , t, k ∈ A e d1 = ax1 + by1 = ctx1 + cky1 = c(tk1 + ky1 ), o que implica
que N (c) ≤ N (c(tx1 + ky1 )) = N (d1 ). Logo, d1 é um máximo divisor comum de a e
b. Não é difícil mostrar que quaisquer dois máximos divisores comuns de a e b são
associados. Assim, d = d1 u, u é unidade de A, e d = (ax1 + by1 )u, o que nos dá
d = a(x1 u) + b(y1 u). Portanto, temos d = ax0 + by0 , onde x0 = x1 u, y0 = y1 u.
(iii) Suponha que existam x0 , y0 ∈ A tais que 1A = ax0 + by0 . Como d =
mdc(a, b), então d|a e d|b. Logo, a = dt e b = dk, t, k ∈ A. Assim, 1A = dtx0 +dky0 ,
ou ainda, 1A = d(tx0 + ky0 ). Portanto, d é uma unidade de A e 1A = mdc(a, b).
Observação 1.1 Em particular, o resultado do Teorema 1.4 é válido para o anel
dos números inteiros Z e para o Anel dos Inteiros Gaussianos Z[i].
ax + by = c, as chamadas equações diofantinas,
a e b não nulos. Procuremos soluções
x0 , y0 ∈ Z tais que ax0 + by0 = c.
Consideremos equações da forma
onde
a, b
e
c
são números inteiros, sendo
inteiras, isto é, pares de números
1.2
Anel dos Inteiros Gaussianos
8
Proposição 1.1 Sejam a, b e c inteiros e d = mdc(a, b). A equação diofantina
ax + by = c tem soluções se, e somente se, d | c.
Dem.: Consideremos o conjunto I de todos os valores que o primeiro membro
pode assumir, isto é, I = {ax + by|x, y ∈ Z}. Não é complicado ver que I é um ideal
de Z e que se d = mdc(a, b), temos I = dZ. Obviamente, a equação tem solução se,
e somente se, c ∈ I , e isso acontece se, e somente se, d | c.
Veremos agora como encontrar todas as soluções de uma equação diofantina no
caso em que existem soluções.
Teorema 1.5 Sejam a, b e c inteiros tais que d = mdc(a, b) divide c. Escrevendo d
na forma d = ra + sb, com r, s ∈ Z, temos que x0 = r dc , y0 = s dc é uma solução da
equação ax + by = c. Toda outra solução é da forma x = x0 + db t, y = y0 − ad t, com
t ∈ Z. E, reciprocamente, para todo t ∈ Z, os valores x e y dados pelas fórmulas
acima são soluções da equação.
Dem.: Se d = ra+sb, multiplicando ambos os membros por dc , temos que (r dc )a+
c
(s d )b = d dc = c. Logo, x0 = r dc , y0 = s dc é uma solução. Devemos provar agora que
todo par de inteiros da forma dada no enunciado é solução e, reciprocamente, que
toda solução é dessa forma. De fato, dados x = x0 + db t, y = y0 − ad t, substituindo
na equação, temos:
a
ab
ab
b
a(x0 + t) + b(y0 − t) = ax0 + t + by0 − t = ax0 + by0 = c
d
d
d
d
.
Seja agora (x0 , y 0 ) uma solução. Mostraremos que existe t ∈ Z tal que x0 =
x0 + db t, y 0 = y0 − ad t. Como (x0 , y 0 ) é solução, temos que ax0 + by 0 = c = ax0 + by0 ,
donde a(x0 −x0 ) = b(y0 −y 0 ). Escrevendo a = a1 d e b = b1 d, temos que mdc(a1 , b1 ) =
mdc( ad , db ) = 1. Dividindo a expressão acima por d, vem que
a1 (x0 − x0 ) = b1 (y0 − y 0 )(∗)
Em particular, b1 | a1 (x0 − x0 ). Como mdc(a1 , b1 ) = 1, do Teorema de Euclides,
temos que b1 | (x0 − x0 ) e existe t ∈ Z tal que x0 − x0 = b1 t, isto é, x1 = x0 + db t.
Ainda, substituindo x0 − x0 por b1 t na relação (*), temos a1 b1 t = b1 (y0 − y 0 ), donde
y 0 = y0 − a1 t = y0 − ad t.
1.2
Anéis Quocientes de Inteiros Gaussianos
Nesta seção, apresentamos alguns resultados que serão utilizados na representação de grafos Gaussianos.
1.2
Anel dos Inteiros Gaussianos
9
Por simplicidade de notação, dado
α ∈ Z[i],
denotaremos o quociente
Z[i]
por
(α)
Z[i]α .
Teorema 1.6 Seja 0 6= α = a + bi ∈ Z[i]. Então Z[i]α possui N (α) = a2 + b2
elementos.
Dem.: Seja
α 6= 0 um inteiro Gaussiano e N = N (α). Armamos que Z[i]N
possui N elementos. De fato, se β = b1 + b2 i e β 0 = b01 + b02 i são congruentes módulo
N , então existem β 00 = b001 + b002 i tal que β − β 0 = β 00 N , o que acarreta b1 − b01 = b001 N
e b2 − b02 = b002 N . Assim, b1 ≡ b01 (mod N ) e b2 ≡ b02 (mod N ). Portanto, existem N 2
possibilidades para os coecientes de β .
Como N (α) = αα, então (N (α)) = (αα) ⊆ (α). Esta última inclusão é válida, pois, para todo β ∈ Z[i], βαα é múltiplo de α. Assim, pelo Exemplo 1.4, temos:
Z[i]
(αα) ∼ Z[i]
e | Z[i] | = nm, onde n = | (α) | e m = | Z[i] |. Finalmente, a seguinte trans(α) =
2
(αα)
(α)
(αα)
(αα)
(α)
(α)
formação f : Z[i]
→ (αα)
denida por f (β + (α)) = βα + (αα) é um isomorsmo e
(α)
Z[i]
Z[i]
os quocientes (α) e (α) têm o mesmo número de elementos.
Teorema 1.7 Seja α = a + bi ∈ Z[i] e N = a2 + b2 a norma de α. Então ZN e
Z[i]α são anéis isomorfos se, e somente se, mdc(a, b) = 1.
Dem.: Se ZN e Z[i]α são anéis isomorfos, denotaremos por f : Z[i]α → ZN
o isomorsmo. Suponha que mdc(a, b) = d 6= 1. Então d | a e d | b, ou seja,
é um inteiro. Além disso, 1 < d implica 0 < N (α)
< N.
d | a2 + b2 = N (α) e N (α)
d
d
N (α)
N (α)
N (α)
N (α)
Com isso, f ( d ) = d f (1) = d 6= 0 (mod N ). Por outro lado, d ≡ α αd ≡
0 (mod α), de onde obtemos que f (0) 6= 0, uma contradição com o fato de f ser um
isomorsmo de anéis.
Suponha agora que mdc(a, b) = 1 e considere a função µ : ZN → Z[i]α dada
por µ(g) = g (mod α). Para provar que µ está bem denida, tome g, g 0 ∈ ZN tais
que g ≡ g 0 (mod N ). Então existe z ∈ Z tal que g − g 0 = zN = zαα. Portanto,
g ≡ g 0 (mod α).
µ é injetora, pois se µ(g) ≡ 0 (mod α), então g ≡ 0 (mod N ). Seja µ(g) = g = βα,
com β = x + yi ∈ Z[i]. Então de g = (x + yi)(a + bi) = (xa − yb) + (xb + ya)i
obtemos: xa − yb = g, xb + ya = 0. Assim, (x, y) = (−at, −bt), t ∈ Z. Portanto,
g = −ata − btb = (−t)(a2 + b2 ) = (−t)N . Logo, g ≡ 0 (mod N ).
µ é sobrejetora. De fato, considere γ = x + yi e um par de inteiros x0 , yo tais
que x0 b + y0 a = −y . Isso é válido pois, como supomos mdc(a, b) = 1, existem dois
números x0 e y 0 tais que ax0 + by 0 = 1. Multiplicando ambos os lados da última igualdade por (−y), obtemos ax0 + by0 = −y , onde x0 = x0 (−y) e y0 = y 0 (−y). Então
(x + yi) + (x0 + y0 i)(a + bi) = (x + x0 a − y0 b) + (y + y0 a + x0 b)i = x + x0 a − y0 b. Este
é um inteiro congruente a γ módulo α. Portanto, µ(x + x0 a − y0 b) = x + x0 a − y0 b ≡
γ (mod α).
1.2
Anel dos Inteiros Gaussianos
10
Corolário 1.1 Seja 0 6= α ∈ Z[i]. Então:
(α)
i) Se β ∈ Z[i] divide α, então o ideal (β) ⊆ Z[i]α possui N
elementos.
N (β)
ii) Tomando β ∈ Z[i] tal que β não divide α e γ = mdc(α, β), então o ideal
(α)
(β) ⊆ Z[i]α é gerado por γ e possui N
elementos.
N (γ)
Dem.:
i) Como β divide α, então (α) ⊆ (β). Assim,
Z[i]
(α)
(β)
(α)
∼
=
Z[i]
(β)
. Logo,
β
α
possui
N (α)
N (β)
β
α
é um ideal de
Z[i]
(α)
e temos:
elementos.
ii) Considere γ = mdc(α, β). Como Z[i]α é um domínio euclidiano, então, pelo
Teorema 1.4, existem γ1 , γ2 ∈ Z[i] tais que γ = γ1 β + γ2 α. Assim, γ ≡ γ1 β (mod α),
o que implica a inclusão (γ) ⊆ (β). Por outro lado, γ divide β . Com isso, (β) ⊆ (γ).
Logo, (β) é gerado por γ = mdc(α, β). Como (γ) ⊆ Z[i]α , pelo item i, (β) = (γ)
possui NN (α)
elementos.
(γ)
Lema 1.1 Seja 0 6= a + bi ∈ Z[i]. Então x + yi ≡ x0 + y0 i (mod a + bi) se, e somente
se, existem u, v ∈ Z tais que x0 = x + ua − vb e y 0 = y + ub + va.
Dem.: De fato:
x − x0 + yi − y 0 i = (u + vi)(a + bi), u, v ∈ Z ⇔
x − x0 + (y − y 0 )i = ua + ubi + avi − vb, u, v ∈ Z ⇔
x − x0 + (y − y 0 )i = ua − vb + (ub + va)i − vb, u, v ∈ Z
A primeira signica que x + yi ≡ x0 + y 0 i (mod a + bi) e a última assegura que
x0 = x + ua − vb e y 0 = y + ub + va.
Teorema 1.8 Sejam a, b ∈ Z tais que 0 < a ≤ b e dois conjuntos denidos como:
i) Sa = {x + yi ∈ Z[i] | 0 ≤ x ≤ a − 1 e 0 ≤ y ≤ a − 1}
ii) Sb = {x + yi ∈ Z[i] | a ≤ x ≤ a + b − 1 e 0 ≤ y ≤ b − 1}.
Então D = Sa ∪ Sb é um sistema residual reduzido de Z[i]α .
Dem.: Sabemos que um sistema residual reduzido de Z[i]α , com 0 6= α = a + bi,
possui a2 + b2 elementos. Como |D| = |Sa ∪ Sb | = |Sa | + |Sb | − |Sa ∩ Sb | = a2 + b2 − 0,
basta provar que os elementos de D são diferentes módulo α. Dados η = x + yi, η 0 =
x0 + y 0 i ∈ D, tais que η ≡ η 0 (mod α), devemos mostrar que η = η 0 . Pelo Lema 1.1,
temos: x + yi ≡ x0 + y 0 i (mod α) se, e somente se, x − x0 = ua − vb e y − y 0 = ub + va,
onde u, v ∈ Z.
Há três possibilidades para o produto uv : uv > 0, uv < 0 ou uv = 0.
No primeiro caso (uv > 0), como a ≥ 0 e b ≥ 0, com a, b ∈ Z, então temos: |y − y 0 | = |ub + va| = |v|a + |u|b ≥ a + b. Mas y, y 0 ∈ {0, . . . , b − 1}, então
|y − y 0 | ≤ b − 1 < a + b, o que é uma contradição. Logo, uv > 0 não ocorre.
1.2
Anel dos Inteiros Gaussianos
11
Para o caso uv < 0, temos |x − x0 | = |ua − vb| = |u|a + |v|b ≥ a + b > a + b − 1.
Como x, x0 ∈ {0, . . . , a + b − 1}, então |x − x0 | ≤ a + b − 1, o que também é uma
contradição. Dessa forma, uv < 0 não ocorre.
Podemos considerar então uv = 0. Suponha que u = 0, então x − x0 = −vb e
y−y 0 = va. Como |x−x0 | < a+b, a primeira condição nos dá |−vb| = |x−x0 | < a+b.
Assim, |v|b < a+b e, consequentemente, |v| < ab +1 ≤ 2, o que nos dá |v| < 1. Logo,
para u = 0 há três casos para v . Se v = 1, então temos: x − x0 = −b e y − y 0 = a,
ou ainda, x = x0 − b e y = y 0 + a. Por outro lado, já sabemos que 0 ≤ x0 ≤ a + b − 1,
então somando −b nas desigualdades obtemos x ≤ a − 1, o que obriga η ∈ Sa . Mas,
da igualdade y = y 0 + a, tiramos que η ∈ Sb , pois b − 1 ≥ y = y 0 + a ≥ a > a − 1, o
que impede η ∈ Sa . Agora, de Sa ∩ Sb = ∅, obtemos uma outra contradição. O caso
v = −1 pode ser analisado de forma análoga. Finalmente, supomos v = 0, então
temos |ub + va| = |u|b. Como |y − y 0 | < b, esta condição força u = 0. Portanto, a
única possibilidade é que x = x0 e y = y 0 .
Capítulo 2
Grafos Circulantes e Gaussianos
2.1
Fatos básicos sobre Grafos
As redes interligadas nas quais faremos o roteamento serão modeladas por meio
de grafos circulantes e grafos gaussianos, objetos de estudo neste capítulo. Segundo
Bermond (1995), entre outras aplicações, grafos circulantes podem ser usados em
redes de telecomunicações, no desenvolvimento de circuitos VLSI, e organização de
serviços de memória de vários módulos. Em relação aos grafos Gaussianos, veremos
que são isomorfos aos circulantes sob algumas restrições e que o roteamento neles é
feito com um menor custo computacional. Antes de estudar essas classes de grafos,
serão apresentados alguns conceitos básicos sobre grafos com exemplos ilustrativos.
Como referência, podemos citar Netto (2006).
Denição 2.1 Um grafo G = (V, E) consiste em um conjunto nito não-vazio
V (G) = V de pontos chamados vértices junto com um conjunto E(G) = E de
pares ordenados de pontos distintos de V , chamados de arestas. Um subgrafo de G
é um grafo G0 = (V 0 , E 0 ) com um conjunto de vértices V 0 (G0 ) = V 0 e um conjunto
de arestas E 0 (G0 ) = E 0 tais que V 0 ⊂ V e E 0 ⊂ E .
Exemplo 2.1 Neste exemplo, apresentamos um grafo G = (V, E), onde os vértices
são V = {1, 2, 3, 5, 6, 7, 8} e E = {(1, 2), (2, 3), (3, 5), (5, 6), (6, 7), (2, 7), (7, 8), (8, 1)}.
12
2.1
Grafos Circulantes e Gaussianos
13
Figura 2.1: Exemplo de grafo com 7 vértices
Note que grafos podem ser utilizados para modelar redes da seguinte forma. Para
cada elemento da rede, associamos a um vértice de um grafo e para cada ligação,
existe uma aresta correspondente deste mesmo grafo.
Figura 2.2: Modelagem de redes através de grafos
Denição 2.2 Dado um grafo G = (V, E), se existir e = (u, v) ∈ E , dizemos que
u e v são vértices adjacentes. Mais ainda, o vértice u e a aresta e são incidentes
um com outro, assim como v e e. O grafo G é não-direcionado se para cada par de
vértices (u, v) ∈ E implicar que (v, u) ∈ E . Se o número cardinal de V é n, dizemos
que G tem ordem n.
Para um grafo
incidentes com
de grau
d.
v.
G,
dizemos que o
grau de um vértice v
é o número de arestas
d, G é chamado regular
G é rotulado se os seus n vértices são distinguidos
Se todos os vértices têm o mesmo grau
Dizemos que um grafo
uns dos outros por rótulos.
Exemplo 2.2 Neste exemplo, temos um grafo no qual cada um dos vértices está
ligados a outros 3 vértices. Portanto, todos têm grau 3 e podemos dizer que o grafo
é de grau 3.
2.1
Grafos Circulantes e Gaussianos
14
Figura 2.3: Exemplo de grafo de grau 3
Denição 2.3 A matriz de adjacências A = [aij ], de um grafo rotulado G com n
vértices é a matriz n × n na qual aij = 1 se vi é adjacente a vj e aij = 0 caso
contrário.
Assim, há uma correspondência um a um entre grafos rotulados de ordem
n e as
matrizes binárias simétricas com diagonal nula, ou seja, aquelas matrizes de ordem
n × n, onde as entradas são
aii = 0, ∀i = {0, 1, . . . , n}.
todas iguais a 1 ou 0, valem a igualdade
aij = aji
e
Denição 2.4 Dois grafos G = (V, E) e H = (V 0 , E 0 ) são isomorfos se existir uma
bijeção entre os conjuntos de vértices: φ : V → V 0 que preserva adjacências, ou
seja, se dois vértices v1 , v2 ∈ V são adjacentes em G, então φ(v1 ) e φ(v2 ) devem ser
adjacentes em H . Denotamos que os grafos G e H são isomorfos por G ∼
= H.
Observação 2.1 Um isomorsmo φ de um grafo G nele mesmo é chamado automorsmo.
Exemplo 2.3 Os dois grafos deste exemplo são isomorfos se considerarmos a função
φ : {1, 2, 3, 4} → {a, b, c, d} tal que φ(1) = a; φ(2) = b; φ(3) = c; φ(1) = d.
2.1
Grafos Circulantes e Gaussianos
15
Figura 2.4: Exemplo de dois grafos isomorfos
Denição 2.5 Uma cadeia de um grafo G é uma sequência alternada de vértices
e arestas v0 , e1 , v1 , . . . , vn−1 , en , vn na qual cada aresta é incidente com dois vértices
que imediatamente a procede e a segue. Esta cadeia liga v0 e vn e também pode ser
indicada apenas pelos vértices como v0 v1 . . . vn . A cadeia é chamada de caminho se
todos os vértices são diferentes e de ciclo se v0 = vn . Observe que uma cadeia pode
ser vista como um subgrafo de G.
Um grafo
G
é conexo se qualquer par de vértices é ligado por um caminho.
Podemos denir o comprimento de um caminho
arestas que ocorre nele e a distância
D(u, v)
v0 v1 . . . vn
como
entre dois vértices
u
e
n, o número de
v em G como o
comprimento de um caminho mais curto que os ligam.
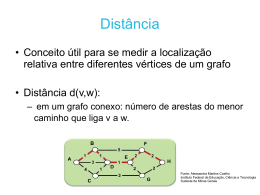
Exemplo 2.4 Na ilustração a seguir, temos um grafo conexo. Se considerarmos
nele o caminho 1 2 3 4, que liga os vértices 1 e 4, seu comprimento é 3. Mas esse
não é o menor caminho ligando esses vértices, pois podemos considerar também o
caminho 1 0 4, cujo comprimento é 2. Assim, temos D(1, 4) = 2. Note ainda que
neste mesmo grafo temos o exemplo de um ciclo, que é o caminho 0 1 2 3 4 0
Figura 2.5: Grafo conexo
2.1
Grafos Circulantes e Gaussianos
16
Observação 2.2 Em um grafo conexo G = (V, E) a distância é uma métrica, isto
é, ocorre para quaisquer vértices u, v, w ∈ V :
i) D(u, v) ≥ 0, com D(u, v) = 0 se, e somente se, u = v .
ii) D(u, v) = D(v, u).
iii) D(u, v) + D(v, w) ≥ D(u, w).
Dem.: As duas primeiras são de fácil vericação. Demonstra-se a terceira
supondo que existam vértices u0 , v0 e w0 tais que D(u0 , v0 ) + D(v0 , w0 ) < D(u0 , w0 ).
Assim, existiriam um menor caminho u0 a1 a2 . . . v0 de tamanho n ligando u0 a v0
e um menor caminho v0 b1 b2 . . . w0 de tamanho m ligando v0 a w0 . Mas o caminho
u0 a1 a2 . . . v0 b1 b2 w0 tem tamanho m + n e liga u0 a w0 , o que contradiz a hipótese de
que o menor caminho ligando u0 a w0 tem tamanho D(u0 , w0 ) maior que D(u0 , v0 )+
D(v0 , w0 ) = m + n.
Denição 2.6 O diâmetro k de um grafo conexo G é o tamanho do maior entre
todos os menores caminhos de cada par de vértices possíveis do grafo.
É fácil vericar que, no Exemplo 2.1, o diâmetro do grafo é 4. No Exemplo 2.2,
o diâmetro é 3. No grafos do Exemplo 2.3, o diâmetro é 1 e no 2.4, temos um grafo
cujo diâmetro é 4.
Denição 2.7 Dois vértices u e v são similares se para algum automorsmo α de
G, ocorrer α(u) = v . Da mesma forma, duas arestas (u1 , v1 ), (u2 , v2 ) são similares
se existir um automorsmo α de G tal que α(u1 , v1 ) = (u2 , v2 ).
Denição 2.8 Um grafo é vértice-simétrico se qualquer par de vértices é similar e
é aresta-simétrico se qualquer par de arestas é similar. Ele será simétrico se for ao
mesmo tempo vértice-simétrico e aresta-simétrico.
Observação 2.3 A distância média k de um grafo vértice-simétrico pode ser cal-
culada como
P
k :=
D(u,u0 )
u6=u0
u∈V
]V − 1
,
onde u0 é um vértice qualquer xado e ]V é o número de elemento de V , ou seja, a
ordem do grafo. De fato, considerando u0 e v0 então devemos ter a igualdade
P
D(u,u0 )
u6=u0
u∈V
]V − 1
P
=
D(v,v0 )
v6=v0
v∈V
]V − 1
2.2
Grafos Circulantes e Gaussianos
17
pois, como o grafo é simétrico, existe um automorsmo α tal que α(v0 ) = u0 , o que
implica
P
P
P
D(u,u0 )
u6=u0
u∈V
.
2.2
D(α(v),α(v0 ))
= v6=v0
D(v,v0 )
= v6=v0
v∈V
v∈V
Grafos Circulantes
Apresentamos nesta seção uma classe de grafos que será objeto de estudos neste
trabalho, os grafos circulantes. Trata-se de uma classe especíca de uma classe mais
geral, os grafos de Cayley, que são denidos a seguir.
Denição 2.9 Dado um grupo G nito e S ⊂ G , o grafo de Cayley Cay(G, S) é o
grafo com conjunto de vértices V = G e o conjunto de arestas E = {(x, y)|x, y ∈
G, ∃s ∈ S; y = xs}.
Pela denição, podemos mostrar que se
onde 1 é o elemento neutro do grupo
s ∈ S,
então
(1, s) ∈ E
e
(s−1 , 1) ∈ E ,
G.
Denição 2.10 Um grafo circulante com N vértices e saltos {j1 , j2 , . . . , jm } é um
grafo não-direcionado no qual cada vértice n, 0 ≤ n ≤ N − 1, é adjacente a todos os vértices n ± ji (mod N ), com 1 ≤ i ≤ m. Denotamos este grafo como
CN (j1 , j2 , . . . , jm ).
Note que grafos circulantes são grafos de Cayley sobre grupos cíclicos. De fa-
CN (j1 , . . . , jk ). Considere G um grupo cíclico G =
{aj1 , . . . , ajk } ⊂ G . Provemos que ocorre o isomorsmo de grafos Cay(G, S) ∼
= CN (j1 , . . . , jk ). Sabemos da denição que o conjunto
E das arestas de Cay(G, S) é:
{(a0 , aj1 ), . . . , ((a0 , ajk ), (a1 , aj1 +1 ), . . . , (a1 , ajk +1 ), . . . , (aN −1 , aj1 +N −1 ), . . . ,
(aN −1 , ajk +N −1 )}.
0
Por outro lado, o conjunto E das arestas do grafo circulante CN (j1 , . . . , jk ) é
to, tome o grafo circulante
{a0 , a1 , a2 , . . . , aN −1 } e S =
dado por:
{(0, j1 ). . . . , (0, jk ), (1, j1 + 1), . . . , (1, jk + 1), . . . , (N − 1, j1 + N − 1), . . . , (N −
1, jk + N − 1)}.
j
Agora basta tomar a seguinte correspondência entre os vértices: a → j (mod N )
0
q
jm +q
e a correspondência entre as arestas f : E → E , dada por f (a , a
) = (q, jm +
q), q = 0, . . . , N − 1.
Proposição 2.1 O grafo de Cayley Cay(G, S) é conexo se, e somente se, S gera G .
Dem.: Suponha Cay(G, S) conexo. Considere g ∈ G e s ∈ S 6= ∅. Então existe
um caminho que liga g a s, digamos gh1 . . . hn s. Sendo g e h1 adjacentes, existe
s1 ∈ S tal que h1 = gs1 , ou seja, g = h1 s−1
1 . Da mesma forma, sendo h1 e h2
2.2
Grafos Circulantes e Gaussianos
18
adjacentes, existe s2 ∈ S tal que h2 = h1 s2 , o que nos dá h1 = h2 s−1
2 . Seguindo o
mesmo raciocínio para o restante do caminho, então existe sn ∈ S tal que h = hn sn ,
−1
−1 −1
−1 −1 −1
ou seja, hn = ss−1
n . Assim, temos: g = h1 s1 = (h2 s2 )s1 = ((h3 s3 )s2 )s1 =
−1
−1
−1
ss−1
n . . . s3 s2 s1 , isto é, qualquer elemento g tomado em G é gerado por elementos
de S ou inversos de elementos desse mesmo conjunto.
Suponha agora que G = hSi. Tome dois elementos g, h de G . Assim, g =
−1
s1 s2 . . . sn e h = t1 t2 . . . tm , onde si ∈ G ou s−1
1 ∈ S e tj ∈ S ou tj ∈ S para todo
i ∈ {1, . . . , n} e j ∈ {1, . . . , m}. Por outro lado, em um grafo de Cayley Cay(G, S),
se x, y são tais que x = ys, onde s ∈ S ou s−1 ∈ S , então (x, y) ∈ E ou (y, x) ∈ E ,
isto é, x e y estão ligados (E é o conjunto das adjacências). Com isso, g está ligado a s1 s2 . . . sn−1 , pois g = s1 s2 . . . sn e sn ∈ S ou s−1
n ∈ S . É fato também que
s1 s2 . . . sn−1 está ligado a s1 s2 . . . sn−2 pois sn−1 ∈ S ou s−1
n−1 ∈ S . Continuando com
o mesmo raciocínio, é possível ligar g a s1 , e de forma análoga, também é possível
−1
ligar h a t1 . Como s1 ∈ S ou s−1
1 ∈ S e t1 ∈ S ou t1 ∈ S , então s1 e t1 estão
−1
ligados a 1. De fato, dado s ∈ S ou s , então s = 1s e (1, s) ∈ E no primeiro
caso (s ∈ S ) e 1 = ss−1 e (s, 1) ∈ E no segundo (s−1 ∈ S ). Portanto, g está ligado
a s1 , que está ligado a 1 e 1 está ligado a t1 , que por sua vez está ligado a h. Logo,
g e h estão ligados.
2.2.1
Algoritmo de Euclides Estendido
Nesta subseção, apresentamos um algoritmo que auxiliará no roteamento de
grafos circulantes. Trata-se de uma adaptação do conhecido Algoritmo de Euclides,
que é utilizado para encontrar o máximo divisor comum entre dois números inteiros
diferentes de zero.
d =
mdc(a, b). Sejam q ≡ a (mod d) e r o inteiro tal que a = rb+q , ou seja, q = a−rb. O
Algoritmo de Euclides é baseado na aplicação repetida da fórmula d = mdc(a, b) =
mdc(b, q). Suponha que a chamada recursiva com argumentos b e q também retorna
inteiros k e l tais que d = kb + lq . Lembrando da denição de r , temos d = kb + lq =
kb + l(a − rb) = la + (k − lr)b. Assim, temos: d = ia + jb, para i = l e j = k − lr.
Esta última equação sugere um método de determinar os inteiros i e j . Este
Sejam
a
e
b
inteiros positivos, e denote com
d
seu maior divisor comum:
método, conhecido como Algoritmo Estendido de Euclides, é mostrado a seguir.
Algoritmo ExtendedEuclidGCD(a,b):
Entrada: inteiros não-negativos
Saída: Tripla de inteiros
(d, i, j)
a
e
b.
tais que
b = 0, então
(a, 1, 0);
q ← a (mod b)
Seja r o inteiro tal que a = rb + q
(d, k, l) ← ExtendedEuclidGCD(b, q)
Se
retorna
d = mdc(a, b) = ia + jb.
2.3
Grafos Circulantes e Gaussianos
retorna
19
(d, l, k − lr)
O código-fonte do Algoritmo de Euclides Estendido é apresentado no Anexo
deste trabalho como função auxiliar, na seção que trata do roteamento de grafos
circulantes.
Proposição 2.2 Um grafo circulante CN (j1 , j2 , . . . , jm ) é conexo se, e somente se,
ocorrer a igualdade mdc(j1 , j2 , . . . , jm , N ) = 1.
Dem.: Considere CN (j1 , j2 , . . . , jm ) igual ao grafo de Cayley Cay(G, S), sendo
G o grupo cíclico {1, a, . . . , aN −1 } e S = {aji , . . . , ajm }. Já foi provado na Proposição
2.1 que Cay(G, S) é conexo se, e somente se, S gera G . Isso é o mesmo que dizer que
para a ∈ G , existem k1 , k2 , . . . , km ∈ Z tais que a = ak1 j1 ak2 j2 . . . akm jm , ou seja, 1 ≡
(k1 j1 +k2 j2 +. . .+km jm ) (mod N ), equivalente a: 1 = (k1 j1 +k2 j2 +. . .+km jm )+kN ,
onde k1 , k2 , . . . km , K ∈ Z. Portanto, mdc(j1 , j2 , . . . , jm , N ) = 1.
Lema 2.1 Seja G = Cay(G, S) um grafo de Cayley. Então G é circulante se, e
somente se, G é cíclico.
Dem.: A volta é uma consequência direta da denição de grafos circulantes.
Suponha que o grafo Cay(G, S) é circulante. Assim, o grau do grafo d é o cardinal
de S e a ordem N é o cardinal de G . Então Cay(G, S) ∼
= CN (j1 , . . . jd ) para alguns
inteiros diferentes j1 , . . . , jd . Denotemos por f : G → ZN o isomorsmo de grafos
entre Cay(G, S) e CN (j1 , . . . jd ). Pela denição de isomorsmo de grafo, temos:
y = x + si se, e somente se, f (y) = f (x) + jk , onde i = 1, . . . , d. Podemos assumir
sem perda de generalidade que f (si ) = f (ji ) para i = 1, . . . , d. Note que, como consequência f (msi ) = f (m)f (si ) = f (m)ji . Além disso, f (0G ) = 0ZN . Sejam
x, y ∈ G
P
dois vértices. Como Cay(G, S) é conexo, existem xi , yi ∈ Z tais que x = di=1 xi si e
P
P
P
P
y = di=1 yi si . Agora, f (x + y) = f ( di=1 xi si + di=1 yi si ) = f ( di=1 (xi + yi )si ) =
Pd
Pd
i−1 f (xi + yi )f (si ) =
i−1 (f (xi ) + f (yi ))f (si ) = f (x) + f (y), o que implica que f
é um isomorsmo de grupos. Portanto, G é cíclico.
2.3
Grafos Gaussianos
Denição 2.11 Seja 0 6= α ∈ Z[i]. Denimos o grafo gaussiano gerado por α,
Gα = (V, E), como segue:
i) V = Z[i]α é o conjunto de vértices.
ii) E = {(η, β) ∈ V × V |β − η ≡ ±1, ±i (mod α)} é o conjunto de arestas.
2.3
Grafos Circulantes e Gaussianos
20
Pela denição, grafos gaussianos têm ordem
quando
N (α) = 1,
N (α), são regulares de grau 4, exceto
são não-direcionados, conexos e vértices-simétricos. De fato, são
regulares, pois se possuírem mais de quatro elementos, então cada vértice é conec-
(η, β) ∈ V × V ,
(η − β) = −(β − η) ≡ ±1, ±i (mod α),
tado a quatro outros vértices. Eles são não-direcionados, pois se
β − η ≡ ±1, ±i (mod α). Assim, temos
ou seja, (β, η) ∈ V × V . Segue ainda da denição que grafos gaussianos sempre
possuem o 0 ∈ Z[i]. Dessa forma, dado qualquer elemento α = a + bi, vértice do
grafo, então ele está conectado a a − 1 + bi, que está conectado a a − 2 + bi, que por
sua vez está ligado por um caminho a a − a + bi. Este último está ligado a (b − 1)i
que, pelo mesmo raciocínio, está ligado a 0i = 0. Como todos estão ligados ao 0, é
possível tomar um caminho ligando quaisquer dois vértices passando pelo próprio 0.
então
Denição 2.12 Um Grafo Toroidal com b2 vértices pode ser denido como Tb =
(V, E), onde V = Zb × Zb e dois vértices (n, m), (n0 , m0 ) ∈ V são adjacentes se, e
somente se, n = n0 e m − m0 ≡ ±1 (mod b) ou m = m0 e n − n0 ≡ ±1 (mod b).
Mais adiante, veremos que os grafos circulantes, da seção anterior, e toroidais
classicam os grafos gaussianos.
O Lema seguinte nos gera condições necessárias e sucientes para dois grafos
gaussianos serem isomorfos.
Lema 2.2 Dados a + bi, c + di ∈ Z[i], então Ga+bi ∼
= Gc+di se, e somente se, existe
u ∈ {±1, ±i} tal que a + bi = u(c + di) ou (a − bi) = u(c + di), isto é, c + di é
associado a a + bi ou a − bi.
Conforme o Lema 2.2, podemos assumir que qualquer grafo gaussiano é gerado
0 6= α = a + bi ∈ Z[i] tal que 0 ≤ a ≤ b. De fato, se Ga+bi
a > b, então existe um outro grafo gaussiano gerado por c + di, com c ≤ d,
isomorfo a Ga+bi . Da mesma forma, se Ga+bi for qual que a < 0 ou b < 0, então
existe um grafo Gc+di isomorfo a Ga+bi , onde 0 < c.
por um inteiro gaussiano
é tal que
Sejam a, b ∈ Z tais que 0 < a ≤ b e D = Sa ∪ Sb , onde Sa = {x + yi ∈ Z[i] | 0 ≤
x ≤ a − 1 ∧ 0 ≤ y ≤ a − 1} e Sb = {x + yi ∈ Z[i] | a ≤ x ≤ a + b − 1 ∧ 0 ≤ y ≤ b − 1}
2
2
(já denidos no Teorema 1.8). Sabemos que o número de elementos de D é a + b .
É possível construir um grafo G = (D, E) da seguinte forma:
2
2
2
2
1) Arranje os a + b vértices em dois quadrados justapostos de tamanhos a e b
de forma que estejam alinhados na parte inferior e o quadrado menor que do lado
esquerdo. O vértice localizado no canto inferior esquerdo será o
x + yi
se estiverem
x
posições à direita do nível do
0
e
y
0
e os demais serão
acima do
0.
2) Ligue cada vértice aos que, se existirem, estão localizados imediatamente acima, abaixo, à direita e à esquerda.
3) Para os vértices
4) Para os vértices
5) Para os vértices
0 ≤ x ≤ b − 1, ligue x + 0i a (x + a) + (b − 1)i.
b ≤ x ≤ a + b − 1, ligue x + 0i a (x − b) + (a − 1)i
0 ≤ y ≤ a − 1, ligue 0 + yi a (a + b − 1) + (y + b − a)i
2.3
Grafos Circulantes e Gaussianos
6) Para os vértices
a ≤ y ≤ b − 1,
ligue
21
x + yi
a
(a + b − 1) + (y − a)i.
2.5.
Considerando, por exemplo, a=5 e b=9, temos o grafo da gura
Figura 2.6: Grafo
Para
Ga+bi ,
com
0 < a ≤ b,
G = (D, E)
já vimos que possui
gulares de grau 4. O próximo teorema diz que
Gα
a2 + b 2
vértices e que são re-
é isomorfo a
G,
anteriormente
construído.
Teorema 2.1 Se 0 < a ≤ b e α = a+bi, então Gα ∼
= G, onde G é o grafo construído
acima.
Dem.: Suponha
Gα = (Z[i]α , E 0 ) e G = (D, E). Pelo Teorema 1.8, temos
Z[i]α = {A + (α)|A ∈ D}. Considere a função: ϕ : D → Z[i]α denida como
ϕ(A) = A + (α).
Obviamente, ϕ está bem denida. Além disso, ela é bijetora. Primeiramente
mostraremos que é injetora. Suponha que A + (α) = B + (α), então A − B ≡
0 (mod α). Daí, segue que A = B . A função ϕ também é sobrejetora, pois se
A + (α) ∈ Z[i]α , então A ∈ D e, assim, ϕ(A) = A + (α).
Para provar que ϕ é um isomorsmo de grafos, resta mostrar que ela preserva adjacências, ou seja, se (A, B) ∈ E , então (ϕ(A), ϕ(B)) ∈ E 0 . Suponha que
A = x + yi e B = x0 + y 0 i.
1o caso: 0 < x < a − 1 e 0 < y < a − 1 ou a < x < a + b − 1 e 0 < y < b − 1
Neste caso, B é ligado a A pelo passo 1. Logo, x0 = x − 1 e y 0 = y (quando
B está imediatamente à esquerda de A) ou x0 = x + 1 e y 0 = y (quando B está
imediatamente à direita de A) ou x0 = x e y 0 = y + 1 (quando B está imediatamente
acima de A) ou ainda x0 = x e y 0 = y − 1 (quando B está imediatamente abaixo
de A). Em todas essas situações, A − B ≡ u (mod α), com u ∈ U (Z[i]). Logo, pela
denição de grafo gaussiano, temos (A + (α), B + (α)) ∈ E 0 .
2.3
Grafos Circulantes e Gaussianos
22
2o caso: 0 < x ≤ b − 1 e y = 0
Neste caso, B pode ter sido ligado a A pelo passo 1 ou pelo passo 2. Se for
pelo passo 1, então x0 = x − 1 e y 0 = y (quando B está imediatamente à esquerda
de A) ou x0 = x + 1 e y 0 = y (quando B está imediatamente à direita de A) ou
x0 = x e y 0 = y + 1 (quando B está imediatamente acima de A). Analogamente ao primeiro caso, a conclusão é que (A + (α), B + (α)) ∈ E 0 . Por outro lado,
se a ligação tiver sido feita pelo passo 2, então x0 = x + a e y 0 = b − 1, ou seja,
B = (x+a)+(b−1)i = x−i+α. Portanto, A−B ≡ −i (mod α) e, consequentemente,
(A + (α), B + (α)) ∈ E 0 .
3o caso: b ≤ x ≤ a + b − 1 e y = 0
Também neste caso, B pode ter sido ligado a A de duas formas. Se for pelo passo 1, então x0 = x − 1 e y 0 = y (quando B está imediatamente à esquerda
de A) ou x0 = x + 1 e y 0 = y (quando B está imediatamente à direita de A) ou
x0 = x e y 0 = y + 1 (quando B está imediatamente acima de A). Analogamente ao primeiro caso, a conclusão é que (A + (α), B + (α)) ∈ E 0 . Por outro lado,
se a ligação tiver sido feita pelo passo 3, então x0 = x − b e y 0 = a − 1, ou seja,
B = x−u+i(a+bi) = x−i+iα. Portanto, A−B ≡ −i (mod α) e, consequentemente,
(A + (α), B + (α)) ∈ E 0 .
4o caso: 0 < y < a − 1 e x = 0
B pode ter sido ligado a A de duas formas. Se for pelo passo 1, então x0 = x + 1
e y 0 = y (quando B está imediatamente à direita de A) ou x0 = x e y 0 = y + 1
(quando B está imediatamente acima de A) ou ainda x0 = x e y 0 = y − 1 (quando B
está imediatamente abaixo de A). Portanto, (A + (α), B + (α)) ∈ E 0 . Se a ligação
tiver sido feita pelo passo 4, então x0 = a + b − 1 e y 0 = y + b − a, ou seja, B =
a+b−1+i(y+b−a) = a+b−1+yi+bi−ai = yi−1+(a+bi)−i(a+bi) = yi−1+(1−i)α.
Como A = yi, então A − B ≡ 1 (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 .
5o caso: x = a e a ≤ y < b − 1
B pode ter sido ligado a A de duas formas. Se for pelo passo 1, então x0 = x + 1
e y 0 = y (quando B está imediatamente à direita de A) ou x0 = x e y 0 = y + 1
(quando B está imediatamente acima de A) ou ainda x0 = x e y 0 = y − 1 (quando B está imediatamente abaixo de A). Portanto, (A + (α), B + (α)) ∈ E 0 . Se
a ligação tiver sido feita pelo passo 5, então x0 = a + b − 1 e y 0 = y − a, ou seja,
B = a+b−1+i(y−a) = a+b−1+yi−ai = a+yi−1+(−i)(a+bi) = a+yi−1+(−i)α.
Como A=a+yi, então A − B ≡ −1 (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 .
6o caso: y = a − 1 e 0 < x < a − 1
B pode ter sido ligado a A de duas formas. Se for pelo passo 1, então x0 = x+1 e
y 0 = y (quando B está imediatamente à direita de A) ou x0 = x − 1 e y 0 = y (quando
2.3
Grafos Circulantes e Gaussianos
23
B está imediatamente à esquerda de A) ou ainda x0 = x e y 0 = y − 1 (quando B está
imediatamente abaixo de A). Portanto, (A + (α), B + (α)) ∈ E 0 . Se a ligação tiver
sido feita pelo passo 3, então x0 = x + b e y 0 = 0, ou seja, B = (x + b) + i(0) = x + b.
Assim, A − B = x + (a − 1)i − (x + b) = ai − b − i = i(a + bi) − i = iα − i, o que
nos diz que A − B ≡ −i (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 .
7o caso: y = b − 1 e a − 1 < x < a + b − 1
B pode ter sido ligado a A de duas formas. Se for pelo passo 1, então x0 = x+1 e
y = y (quando B está imediatamente à direita de A) ou x0 = x − 1 e y 0 = y (quando
B está imediatamente à esquerda de A) ou ainda x0 = x e y 0 = y − 1 (quando B está
imediatamente abaixo de A. Portanto, (A + (α), B + (α)) ∈ E 0 . Se a ligação tiver
sido feita pelo passo 2, então x0 = x − a e y 0 = 0, ou seja, B = x − a + i(0) = x − a.
Assim, A − B = x + (b − 1)i − (x − a) = a + bi + 1 = α + 1. Dessa forma,
A − B ≡ 1 (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 .
0
8o caso: x = a + b − 1 e 0 < y < b − a
B pode ter sido ligado a A de duas formas. Se for pelo passo 1, então x0 = x − 1
e y = y (quando B está imediatamente à esquerda de A) ou x0 = x e y 0 = y − 11
(quando B está imediatamente abaixo de A) ou ainda x0 = x e y 0 = y + 1 (quando B está imediatamente acima de A). Portanto, (A + (α), B + (α)) ∈ E 0 . Se
a ligação tiver sido feita pelo passo 5, então x0 = a e y 0 = y + a, ou seja, B =
a − 1 + i(y + a) = a − 1 + yi + ai. Assim, A − B = a + b − 1 + yi − (a + yi + ai) =
a + b − 1 + yi − a + 1 − yi − ai = b − ai − 1 = (−i)(a + bi) − 1 = (−i)α − 1. Dessa
forma, A − B ≡ −1 (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 .
0
9o caso: x = a + b − 1 e b − a ≤ y < b − 1
B pode ter sido ligado a A de duas formas. Se for pelo passo 1, então x0 = x − 1
e y 0 = y (quando B está imediatamente à esquerda de A) ou x0 = x e y 0 = y − 11
(quando B está imediatamente abaixo de A) ou ainda x0 = x e y 0 = y + 1 (quando
B está imediatamente acima de A). Portanto, (A + (α), B + (α)) ∈ E 0 . Se a ligação
tiver sido feita pelo passo 4, então x0 = 0 e y 0 = y − (b − a), ou seja, B = (y − b + a)i.
Portanto, A − B = a + b − 1 + yi − (y − b + a)i = a + b − 1 + yi − yi + bi − ai =
a + bi + b − ai − 1 = a + bi + (−i)(a + bi) − 1 = (1 − i)(a + bi) − 1 = (1 − i)(α) − 1.
Dessa forma, A − B ≡ −1 (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 .
10o caso: x = 0 e y = 0
B pode ter sido ligado a A de três formas. Se foi ligado pelo primeiro passo,
então B = 1 ou B = i. Logo, A − B é congruente a 1 ou a i módulo α e, portanto,
(A + (α), B + (α)) ∈ E 0 . Se B foi ligado pelo passo 2, então B = a + (b − 1)i e
assim, A − B = 0 − a − (b − 1)i = −a − bi + i = (−1)(a + bi) + i = (−1)α + i.
Logo, A − B ≡ i (mod α) e, consequentemente, (A + (α), B + (α)) ∈ E 0 . Por último,
se B foi ligado a A pelo passo 4, então B = (a + b − 1) + (b − a)i, o que nos dá
A − B = 0 − (a + b − 1) − (b − a)i = −a − b + 1 + ai − bi = ai − b − a − bi + 1 =
2.3
Grafos Circulantes e Gaussianos
24
i(a + bi) − (a + bi) + 1 = (i − 1)(a + bi) + 1 = (i − 1)α + 1. Logo, A − B ≡ 1 (mod α)
e, assim, (A + (α), B + (α)) ∈ E 0 .
11o caso: x = 0 e y = a − 1
B pode ter sido ligado a A de três formas. Se foi ligado pelo passo 1, então
B = 1 + (a − 1)i ou B = (a − 2)i. Logo, A − B = (a − 1)i − 1 + (a − 1)i = −1 ou
A − B = (a − 1)i − (a − 2)i = i. Logo, A − B ∼
= −1 (mod α) ou A − B ∼
= i (mod α) e,
0
portanto, (A + (α), B + (α)) ∈ E . Se B foi ligado pelo passo 3, então B = b + 0i,
o que nos dá A − B = 0 + (a − 1)i − (b + 0i) = ai − i − b = i(a + bi) − i, ou seja,
A − B ≡ −i (mod α) e, assim, (A + (α), B + (α)) ∈ E 0 . Na última possibilidade, B
pode ter sido ligado pelo passo 4, o que nos diz que B = a + b − 1 + (b − 1)i. Assim,
A−B = (a−1)i−(a+b−1+(b−1)i) = ai−i−a−b+1−(b−1)i = ai−i−a−b+1−
bi+i = ai−b−bi−a+1 = i(a+bi)−(a+bi)+1 = (i−1)(a+bi)+1 = (i−1)(α)+1,
ou seja, A − B ≡ 1 (mod α), o que garante que (A + (α), B + (α)) ∈ E 0 .
12o caso: x = a e y = (a − 1)i
A única possibilidade neste caso para que B se ligue a A é pelo passo 1. Então
B = (a−1)+(a−1)i ou B = (a+1)+(a+1)i ou B = a+ai ou ainda B = a+(a−2)i.
Em todas essas situações, A − B ≡ u (mod α), com u ∈ U (Z[i]). Logo, pela denição
de grafo gaussiano, temos (A + (α), B + (α)) ∈ E 0 .
13o caso: x = a e y = b − 1
B pode ter sido ligado a A de três formas. Se a ligação foi através do passo 1, então B = a+(b−2)i ou B = (a+1)+(b−1)i. Logo, A−B = a+(b−1)i−a−(b−2)i = i
ou A − B = a + (b − 1)i − (a + 1) − (b − 1)i = −1. Logo, A − B ∼
= i (mod α) ou
0
∼
A − B = −1 (mod α) e, portanto, (A + (α), B + (α)) ∈ E . Se B foi ligado pelo
passo 2, então B = 0. Assim, A − B = a + (b − 1)i = α − i e, dessa forma,
A − B ≡ −i (mod α), ou seja, (A + (α), B + (α)) ∈ E 0 . A última possibilidade
é B ser ligado pelo passo 5, o que nos dá B = a + b − 1 + (b − 1 − a)i. Então
A − B = a + (b − 1)i − (a + b − 1 + (b − 1 − a)i) = a + bi − i − a − b + 1 − (b − 1 − a)i =
bi − i − b + 1 − bi + i + ai = −b + ai + 1 = (a + bi)i + 1 = αi + 1, ou seja,
A − B ≡ 1 (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 .
14o caso: x = a + b − 1 e y = b − 1
B pode ter sido ligado a A de três formas. Se foi através do passo 1, então
B = a + b − 2 + (b − 1)i ou B = a + b − 1 + (b − 2)i. Logo, A − B = a + b − 1 + (b −
1)i−(a+b−2+(b−1)i) = 1 ou A−B = a+b−1+(b−1)i−(a+b−1+(b−2)i) = i. Logo,
A−B ∼
= 1 (mod α) ou A − B ∼
= i (mod α) e, portanto, (A + (α), B + (α)) ∈ E 0 . Se B
foi ligado pelo passo 2, então B = b−1. Assim, A−B = a+b−1+(b−1)i−(b−1) =
a + b − 1 + bi − i − b + 1 = a + bi − i = α − i. Logo, A − B ≡ −i (mod α) e, consequentemente, (A + (α), B + (α)) ∈ E 0 . A possibilidade restante é de B ter sido ligado
pelo passo 4. Dessa forma, B = (a − 1)i e A − B = a + b − 1 + (b − 1)i − (a − 1)i =
a + b − 1 + bi − i − ai + i = a + bi − ai + b − 1 = (a + bi) + (−i)(a + bi) − 1 =
2.3
Grafos Circulantes e Gaussianos
25
(1 − i)(a + bi) − 1 = (1 − i)α − 1. Com isso, A − B ≡ −1 (mod α) e, portanto,
(A + (α), B + (α)) ∈ E 0 .
15o caso: x = a + b − 1 e 0
Finalmente, B pode ter sido ligado a A através de três formas. Se foi através do
passo 1, então B = a+b−2 ou B = a+b−1+i. Logo, A−B = a+b−1−(a+b−2) = 1
ou A − B = a + b − 1 − (a + b − 1 + i) = −i. Logo, A − B ∼
= 1 (mod α) ou
0
∼
A−B = −i (mod α) e, portanto, (A+(α), B+(α)) ∈ E . Se B foi ligado pelo passo 3,
então B = (a−1)+(a−1)i. Assim, A−B = a+b−1−(a−1)−(a−1)i = b−(a−1)i =
−ai + b − i = (−i)(a + bi) − i = (i)α − i, ou seja, A − B ≡ −i (mod α) e, consequentemente, (A+(α), B +(α)) ∈ E 0 . Por último, se B tiver sido ligado pelo passo 5, então
B = a + ai e A − B = a + b − 1 − (a + ai) = b − 1 − ai = (−i)(a + bi) − 1 = (−i)α − 1.
Portanto, A − B ≡ −1 (mod α) e, com isso, (A + (α), B + (α)) ∈ E 0 .
Teorema 2.2 Seja α = a + bi ∈ Z[i] tal que 0 ≤ a ≤ b, e Gα o grafo gaussiano
gerado por α. Então:
i) Gα ∼
= Ca2 +b2 (a, b) se, e somente se, mdc(a, b) = 1.
ii) Gα ∼
= Tb se, e somente se, a = 0.
Dem.: Sabemos que um grafo circulante é um grafo de Cayley sobre um grupo
cíclico e que, pelo Teorema 1.7, o único caso no qual Z[i]a+bi é cíclico é quando
mdc(a, b) = 1. Também, Z[i]α ∼
= Zb × Zb se, e somente se, a parte real ou a parte
imaginária de α for zero.
Suponha agora que mdc(a, b) = 1. Para o primeiro item, tome α = a + bi.
Temos que CN (α) (a, b) e Gα são grafos isomorfos com o isomorsmo de grafo denido por: Φ : ZN (α) → Z[i]α , com Φ(j) = x + yi (mod α) onde j ≡ ax + by (mod N (α)).
Devemos provar que Φ é uma bijeção que preserva distâncias. Primeiramente, observe que o conjunto de soluções da equação diofantina aX + bY = s(a2 + b2 ) é
{(X, Y ) = (sa + bt, sb − at); t ∈ Z}. Denotemos N = a2 + b2 = N (α).
Primeiramente, mostraremos que Φ está bem denida. Sejam h, j ∈ Z com
h ≡ j (mod N ). Considere j ≡ ax + by (mod N ) e h = ax0 + by 0 (mod N ). Temos que
provar que Φ(j) = Φ(h) (mod α). Assumindo a hipótese, temos a(x−x0 )+b(y −y 0 ) ≡
0 (mod N ), isto é, existe s ∈ Z que verica a(x − x0 ) + b(y − y 0 ) = sN . Agora, se
a(x − x0 ) + b(y − y 0 ) = s(a2 + b2 ), então (x − x0 ) + (y − y 0 )i ≡ 0 (mod α). De fato,
(x−x0 )+(y−y 0 )i = (sa+bt)+(sb−at)i = s(a+bi)+t(b−ai) = s(a+bi)−t(a+bi)i =
(s − ti)(a + bi), de onde é possível concluir esta parte da prova, pois s − ti ∈ Z[i].
Provaremos agora que Φ é injetiva, isto é, que se Φ(j) = Φ(h) (mod α), com
j, h ∈ ZN , então j ≡ h (mod N ). Suponha que Φ(j) = x + yi, Φ(h) = x0 + y 0 i.
Então (x − x0 ) + (y − y 0 )i = γα, com γ ∈ Z[i]. Seja γ = γ1 + γ2 i. Portanto,
(x − x0 ) + (y − y 0 )i = γα = (γ1 a − γ2 b) + (γ1 b + γ2 a)i, então obtemos:
x − x0 = γ1 a − γ2 b ⇒ a(x − x0 ) = γ1 a2 − γ2 ab,
y − y 0 = γ1 b + γ2 a)b(y − y 0 ) = γ1 b2 + γ2 ab.
2.3
Grafos Circulantes e Gaussianos
26
Agora, a(x − x0 ) + b(y − y 0 ) = γ1 (a2 + b2 ), com γ1 ∈ Z, ou seja, j ≡ h (mod N ).
Além disso, Φ é sobrejetiva. Dado um elemento x + yi ∈ Z[i]α , existe j ∈ ZN (α)
tal que j = ax + by e Φ(j) = x + yi.
Para provar o segundo item, apenas considere o isomorsmo de grafo entre o
Torus Tb com b2 vértices e Gb .
Φ0 : Zb × Zb → Z[i]b , com Φ0 (x, y) = x + yi (mod b)
Pelos teoremas anteriores cam bem determinadas as topologias que um grafo
gaussiano pode assumir. Observe que o Teorema 2.2 dá condições para que um grafo
gaussiano seja isomorfo a um grafo circulante. Veja o exemplo a seguir:
Exemplo 2.5 Como mdc(2, 3) = 1, os grafos C1 3(2, 3) e G2+3i são isomorfos.
Figura 2.7: Grafos isomorfos
2.3.1
Diâmetro e Distância média de um grafo Gaussiano
Nesta seção, encontramos expressões gerais para o diâmetro e a distância média
de um grafo gaussiano, que são necessárias nos próximos resultados deste capítulo.
Primeiramente, denimos a distância entre dois vértices em um grafo gaussiano
Gα
pela fórmula
Dα (β, γ) = M in{|x| + |y||(β − γ) ≡ x + yi (mod α)}.
D é uma distância. Para isso, considere β, γ e η ∈ Gα .
i) Dα (β, γ) ≥ 0 e Dα (β, γ) = 0 se, e somente se, β = γ .
De fato, o conjunto {|x| + |y||(β − γ) ≡ x + yi (mod α)} é formado apenas por
números da forma |x| + |y|, que são positivos. Agora, se β = γ , então Dα (β, γ) =
{|x| + |y||0 ≡ x + yi (mod α)}. Como x + yi = 0 + 0i ≡ 0, então o mínimo desse
conjunto será |0| + |0| = 0. Por outro lado, se Dα (β, γ) = 0, então o mínimo do
conjunto {|x| + |y||(β − γ) ≡ x + yi (mod α)} será 0, ou seja, existem x, y tais que
|x| + |y| = 0 e x + yi ≡ β − γ (mod α). Portanto, x, y são nulos e x + yi = 0. Com
isso, 0 ≡ β − γ (mod α) e dessa forma γ ≡ β (mod α).
Provemos que
2.3
Grafos Circulantes e Gaussianos
27
Dα (β, γ) = Dα (γ, β)
β −γ ≡ γ −β (mod α) e assim os conjuntos {|x|+|y||(β −γ) ≡
x + yi (mod α)} e {|x| + |y||(γ − β) ≡ x + yi (mod α)} são iguais.
iii) Dα (β, η) ≤ Dα (β, γ) + Dα (γ, η)
Por denição, Dα (β, γ) = M in{|x| + |y||(β − γ) ≡ x + yi (mod α)} e Dα (γ, η) =
M in{|x| + |y||(γ − η) ≡ x + yi (mod α)}. Sejam então x0 , y 0 tais que |x0 | + |y 0 | é
00
00
um mínimo de {|x| + |y||(β − γ) ≡ x + yi (mod α)} e |x | + |y | é um mínimo de
{|x| + |y||(γ − η) ≡ x + yi (mod α)}. Assim, x0 + y 0 i ≡ β − γ (mod α) e x00 + y 00 i ≡
γ − η (mod α). De onde concluímos que x0 + x00 + (y 0 + y 00 )i ≡ β − η (mod α),
0
00
0
00
ou seja, |x + x | + |y + y | ∈ {|x| + |y||(β − η) ≡ x + yi (mod α)}. Com isso,
Dα (β, η) ≤ |x0 + x00 | + |y 0 + y 00 |. Por outro lado, |x0 + x00 | + |y 0 + y 00 | ≤ |x0 | + |x00 | +
|y 0 | + |y 00 | = Dα (β, γ) + Dα (γ, η). Logo, Dα (β, η) ≤ Dα (β, γ) + Dα (γ, η).
ii)
Isso ocorre porque
Como
Gα
é vértice-simétrico, podemos denir o peso de um vértice (ou sua dis-
tância ao vértice 0) da seguinte forma:
ωα (β) = Dα (β, 0) = M in{|x| + |y||β ≡ x + yi (mod α)}
Para calcular a distribuição de distâncias de um grafo gaussiano é suciente encontrar seu número de vértices de peso
s,
para
s
variando entre
diâmetro do grafo. Este número será denotado por
0
e
k,
onde
k
é o
∆α (s).
Os teoremas a seguir determinam a distribuição de distâncias para grafos gaussianos de ordem par e ímpar, respectivamente.
Mas antes, considere o seguinte
Lema.
Lema 2.3 Dado 0 6= α = a + bi ∈ Z[i], denimos |α| = |a| + |b|.
i) Se 0 6= γ ∈ Z[i], então |α| ≤ |γα|.
ii) Se a < b e 0 6= α ∈ Z[i], então |α| = |γα| se, e somente se, |γ| = 1.
iii) Se γ ∈ Z[i] e 0 ≤ a ≤ b, então se |αγ| < 2b, tem-se |γ| ≤ 1.
Dem.: Seja γ = u + vi ∈ Z[i]. Então γα = (au − bv) + (av + bu)i. Vamos provar
apenas o caso em que a e b são positivos.
(i) Para provar o primeiro item, analisaremos os valores que uv pode assumir:
Se uv > 0, então u e v têm sinais iguais. Caso ambos sejam positivos, temos
|γα| = |au − bv| + |av + bu| ≥ |av + bu| = |av| + |bu| = |a||v| + |b||u| ≥ |a| + |b| = |α|.
A última desigualdade deve-se ao fato de u, v ∈ Z. Se u e v forem inteiros negativos,
então |γα| = |au − bv| + |av + bu| ≥ |av + bu| = | − 1||(av + bu)| = | − (av + bu)| =
| − av − bu| ≥ | − va| + | − ub| ≥ |a||v| + |b||u| ≥ |a| + |b| = |α|.
Se uv < 0, então u e v têm sinais diferentes. Assim, se u é positivo e v negativo,
temos |γα| = |au − bv| + |av + bu| ≥ |au − bv| = |au| + | − bv| ≥ |a| + |b| = |α|.
Por outro lado, se u é negativo e v positivo, então |au − bv| = | − 1||au − bv| =
| − (−au + bv)| = | − au + bv)| ≥ | − au| + |vb| ≥ |a||u| + |v||b| ≥ |a| + |b| = |α|.
Se u = 0 e v 6= 0, então |γα| = | − bv| + |av| = |v||b| + |a||v| = |v|(|a| + |b|) ≥
|a| + |b| = |α|.
Se u 6= 0 e v = 0, então |γα| = |au| + |bu| = |u||a| + |b||u| = |u|(|a| + |b|) ≥
|a| + |b| = |α|.
2.3
Grafos Circulantes e Gaussianos
28
(ii) Para o segundo item, suponha que |γ| = 1. Então |u| + |v| = 1. Como u
e v são inteiros, então |u| = 1 e |v| = 0 ou |u| = 0 e |v| = 1. No primeiro caso,
|γα| = |(au−bv)+(av+bu)i| = |(au)+(bu)i| = |u(a+bi)| = |u||a+bi| = |a|+|b| = |α|.
No segundo caso, |γα| = | − bv + avi| = |v(−b + ai)| = |v(−b + ai)| = |v|| − b + ai| =
|a| + |b| = |α|.
Suponha agora que |α| = |γα|. O conjunto de pontos para os quais a norma
denida no Lema é igual ao valor |α| é dado por {c+di ∈ Z[i], |c|+|d| = |α|}. Vamos
procurar nesse conjunto vetores γ = u + vi tais que |αγ| = |α|. Para isso, iremos
separar o conjunto em 4 partes, sendo cada uma, um segmento de reta localizado em
um dos quadrantes. Cada região possui um vetor representante, que possui norma
idêntica a de α = a + bi. No segundo quadrante, esse vetor é ai − b. No terceiro,
temos −a − bi e no quarto, o vetor é −ai + b (Veja a gura 2.6). É importante
observar que nos complexos, fora dessas regiões, não há outros vetores cuja norma
seja igual à de |α| = |a| + |b|.
Figura 2.8: Pontos cuja norma é igual à
|α|
1o quadrante:
Neste caso, devemos resolver:
a + bi = (u + vi)(a + bi)
a + bi = au − bv + (bu + av)i
Assim,
temos o sistema linear com variáveis inteiras u e v :
a = au − bv
b = bu + av
A solução é u = 1 e v = 0, ou seja, |γ| = 1.
2o quadrante:
Neste caso, devemos resolver:
ai − b = (u + vi)(a + bi)
ai − b = au − bv + (bu + av)i
Da
expressão acima, temos o sistema linear com variáveis inteiras u e v :
−b = au − bv
a = bu + av
A solução é u = 0 e v = 1, ou seja, |γ| = 1.
3o quadrante:
2.3
Grafos Circulantes e Gaussianos
29
Neste caso, devemos resolver:
−a − bi = (u + vi)(a + bi)
−a − bi = au − bv + (bu + av)i
Então
temos o sistema linear com variáveis inteiras u e v :
−a = au − bv
−b = bu + av
A solução é u = −1 e v = 0, ou seja, |γ| = 1.
4o quadrante:
Neste caso, devemos resolver:
−ai + b = (u + vi)(a + bi)
−ai + b = au − bv + (bu + av)i
Logo,
temos o sistema linear com variáveis inteiras u e v :
b = au − bv
−a = bu + av
A solução é u = 0 e v = −1, ou seja, |γ| = 1.
(iii) No último item, temos que x2 +y 2 ≤ (|x|+|y|)2 , então N (γα) ≤ |γα|2 < 4b2 .
Portanto, N (γ) < 4 pois N (α) ≥ b2 . Notando que γ ∈ Z[i], devemos apenas vericar
o caso N (γ) = 2, mas isto é direto para obter que neste caso |γα| = 2b.
Para facilitar as demonstrações dos Teoremas 2.3 e 2.4, usaremos a topologia
losangular para os grafos gaussianos.
Teorema 2.3 Seja 0 6= α = a + bi ∈ Z[i] tal que 0 ≤ a ≤ b, N = a2 + b2 um inteiro
ímpar e t = (a + b − 1)/2 . Então a distribuição de distâncias de Gα é como segue:
i) ∆α (0) = 1.
ii) ∆α (s) = 4s, se 1 ≤ s ≤ t.
iii) ∆α (s) = 4(b − s), se t < s ≤ b − 1.
Dem.: Considere primeiramente 0 6= α = a + bi ∈ Z[i], sendo 0 ≤ a ≤ b e
N = a2 +b2 , um inteiro ímpar. Note que, com essa condição, a razão (a+b−1)/2 ≥ 0
é um número inteiro, pois a2 + b2 ≡ 1 (mod 2) se, e somente se, a + b ≡ 1 (mod 2).
Além disso, ∆α (0) = 1, já que 0 é o único inteiro gaussiano cujo peso é nulo, o que
prova o item (i).
Para o segundo item, temos s variando entre 1 e t. Denotaremos o quadrado do
grafo Gα cujos vérices são −t, ti, t e −ti como Qt = {x+yi ∈ Z[i]||x|+|y| ≤ t} (Veja
a gura 2.6). Dois inteiros gaussianos η 6= η 0 ∈ Qt não são congruentes módulo α.
De fato, se fosse η ≡ η 0 (mod α), teríamos η − η 0 = γα para algum γ ∈ Z[i]. Pelo
lema 2.3, ocorreria |η − η 0 | ≥ |α| = a + b. Mas, pela desigualdade triangular, temos
|η−η 0 | ≤ |η|+|η 0 | ≤ 2t = a+b−1, o que é uma contradição. Além disso, o número de
soluções para a equação |η| = s, com s variando de 1 até t, é a quantidade de vértices
que está nas bordas de Qt , ou seja, 4(s − 1) + 4 = 4s. Dessa forma, está provado o
item (ii). Finalmente, considere os casos s = t+1, . . . , b−1. Primeiramente, observe
que para b = a + 3, os quatro inteiros gaussianos (a + 1) + i, (−a − 1) − i, 1 − (a + 1)i
2.3
Grafos Circulantes e Gaussianos
30
e −1 + (a + 1)i têm peso s = a + 2 = (a + b − 1)/2 + 1 = b − 1 e tais vértices não
pertencem à mesma classe módulo α.
Por outro lado, denoteremos como T o triângulo de vértices t+i, (a+1)+(t−a)i
e t + (t − a)i, conforme a gura 2.6. Na região incluída em T , temos (b − s) inteiros
gaussianos η tais que |η| = s, para s = t + 1, . . . , b − 1. O triângulo T não possui
interseção com a região Qt . Se existirem η ∈ Qt e η 0 ∈ T tais que η − η 0 = αγ . para
0 6= γ ∈ Z[i], então |η − η 0 | ≤ |η| + |η 0 | ≤ t + b − 1 < 2b. Pelo Lema 2.3, temos
que γ ∈ {±1, ±i} e as regiões Qt + αγ e T não possuem interseção. Mais ainda,
as regiões T, −T, iT e −iT não se intersectam como pode ser visto na gura 2.6.
Como η ≡ η 0 (mod α) ⇔ η ≡ η 0 + γα , para qualquer γ ∈ Z[i], podemos considerar
os triângulos T, iT − iα, −T + α e −iT + iα para provar que eles não se intersectam.
Estes triângulos são adjacentes, como pode ser vericado na gura 2.6, e dados dois
vértices η e η 0 nestes triângulos, eles satisfazem |η −η 0 | < 2(t−a) = b−a−1 < a+b.
Portanto, pelo Lema 2.3, η e η 0 não são congruentes módulo α.
Figura 2.9: Translações das Regiões
Q, T, −T, iT
e
−iT
Com o Teorema 2.3, vericamos que para o caso
de pesos
s
N
ímpar temos a seguinte tabela
e o número de vértices com esse peso, denotado por
s
∆α (s)
0 1 2 ···
1 4 8 ···
t
t+1
4t 4(b − t + 1)
···
···
∆α (s):
b−2 b−1
8
4
Tabela 2.1: Distribuição de pesos no caso ímpar
A seguir, temos um exemplo de um grafo gaussiano gerado por α = 2 + 7i.
2
2
Note que seu número de elementos é N = 2 + 7 = 53 e, por isso, podemos
2.3
Grafos Circulantes e Gaussianos
31
aplicar o Teorema 2.3 para determinar sua distribuição de distâncias. Neste caso
= 4. Assim, existem 1 vértice com peso 0; 4 (4 · 1) vértices com peso 1;
t = a+b−1
2
8 (4 · 2) vértices com peso 2; 12 (4 · 3) vértices com peso 3; 16 (4 · 4) vértices com peso
4;
8 (4 · (7 − 5))
vértices com peso
5;
e
4 (4 · (7 − 6))
vértices com peso
6.
Na gura,
cada cor corresponde ao peso dos vértices.
Figura 2.10: Distribuição de pesos no grafo gaussiano gerado por 2 + 7i
Teorema 2.4 Seja 0 6= α = a + bi ∈ Z[i] tal que 0 ≤ a ≤ b, N = a2 + b2 um inteiro
par e t = (a + b)/2 . Quando a < b, a distribuição de distâncias do grafo Gα é como
segue:
i) ∆α (0) = 1.
ii) ∆α (s) = 4s, se 0 < s < t.
iii) ∆α (t) = 2(b − 1).
iv) ∆α (s) = 4(b − s), se t < s < b.
v) ∆α (b) = 1.
Quando 0 < a = b, a distribuição de distâncias do grafo Gb+bi é como segue:
i) ∆α (0) = 1.
ii) ∆α (s) = 4s, se 0 < s < b.
iii) ∆α (b) = 2b − 1.
Dem.: Note que N = a2 + b2 ≡ 0 (mod 2) se, e somente se, a + b ≡ 0 (mod 2).
Com isso, (a + b)/2 é um número inteiro. Além disso, podemos escolher a e b dois
inteiros tais que 0 ≤ a ≤ b e de forma que N = a2 + b2 seja par. Obviamente,
∆α (0) = 1, pois 0 é o único inteiro gaussiano com peso igual a 0. Analogamente ao caso ímpar, as regiões Qt−1 e Qt−1 + γα não se intersectam para qualquer
0 6= γ ∈ Z[i]. Dessa forma, os inteiros gaussianos em Qt−1 pertencem a diferentes
classes módulo α, onde Qt−1 = {η||η| ≤ t − 1}. Portanto, no grafo Gα , temos 4s
elementos de peso s, para s = 1, . . . , t − 1 em Qt−1 , o que prova o segundo item para
ambos os casos.
2.3
Grafos Circulantes e Gaussianos
32
Consideremos agora a < b. Suponha que s = t = (a + b)/2. Neste caso, consideremos os inteiros gaussianos em quatro segmentos de quatro linhas diretas diferentes. Os dois primeiros são os segmentos S1 = A1 B1 e S2 = A2 B2 , onde A1 =
(t − 1) + i, B1 = ti, A2 = (−1 − a) + (t + 1 − b)i e B2 = (1 − t) − i (Veja a gura
2.8).
Figura 2.11: Translações da Região
Qt−1 ,
Segmentos e Triângulo da Prova
Observe que S1 é uma parte da linha direta denida por S = {x + yi|x + y = t}.
O segundo segmento é uma translação por −α do pedaço desta linha. Dessa forma,
temos (S1 −α)∩S2 = ∅. Os dois segmentos à esquerda são R1 = C1 D1 e R2 = C2 D2 ,
onde C1 = −1 + (t − 1)i, D1 = −t, C2 = (t − a − 1) + (−1 − a)i e D2 = 1 + (1 − t)i.
Note que R1 é um pedaço da linha R = {x + yi| − x + y = t} e R2 é uma translação
de −αi do pedaço desta linha. Temos ainda que (R1 − αi) ∩ R2 = ∅. Podemos
vericar que existem exatamente 2(b − 1) inteiros gaussianos no conjunto de pontos
pertencentes a S1 ∪ S2 ∪ R1 ∪ R2 . Mostraremos que para qualquer par de inteiros
gaussianos η, η 0 neste conjunto de pontos não são congruentes módulo α. Como
|η − η 0 | ≤ |η| + |η 0 | ≤ 2t = a + b < 2b, pelo Lema 2.3, temos que η − η 0 = uα, com
u ∈ {±1, ±i}. A partir do comentário anterior é possível perceber que isto nunca
ocorre.
Agora, consideremos os casos s = t + 1, . . . , b − 1. Note apenas que este caso
existe somente quando b ≥ a + 4. Primeiro, note que no caso b = a + 4 os quatro
inteiros gaussianos (a + 1) + 2i, (−a − 1) − 2i, 2 − (a + 1)i e −2 + (a + 1)i têm peso
s = a + 3 = b − 1. Estes inteiros gaussianos não pertencem à mesma classe módulo
α.
Por outro lado, denotaremos o triângulo de vértices (t − 1) + 2i, (t − 1) + (t − a)i
e (a + 1) + (t − a)i como T . Na região T temos (b − s) inteiros gaussianos η tais que
|η| = s, para s = t + 1, . . . , b − 1. Analogamente, para o caso ímpar, o triângulo T
não intersecta a região Qt−1 ∪ S1 ∪ S2 ∪ R1 ∪ R2 ⊂ Qt . Se existirem η ∈ Qt e η 0 ∈ T
tais que η − η 0 = αγ para 0 6= γ ∈ Z[i], então |η − η 0 | ≤ |η| + |η 0 | ≤ t + b − 1 < 2b.
Pelo Lema 2.3, temos que γ ∈ {±1, ±i} e as regiões Qt +αγ e T não se intersectam.
Mais ainda, os triângulos T, −T, iT e −iT não possuem interseção, o que conclui a
prova deste item.
2.3
Grafos Circulantes e Gaussianos
33
Finalmente, os quatro inteiros gaussianos t + (t − a)i, (a − t) + ti, −t + (a − t)i
e (t − a) − ti têm peso b. Os quatro pontos pertecem à mesma classe módulo α,
então selecionamos o primeiro t + (t − a)i como representante de peso b. Para
o caso particular onde 0 < a = b, os dois primeiros itens são provados equivalentemente para o caso a < b. Para o terceiro item, como t = (a + b)/2 = b,
temos que as três regiões especicadas no caso anterior, na verdade são apenas
uma região. Esta região é denida pelos segmentos T1 = E1 F1 e T2 = E2 F2 , onde
E1 = (b − 1) + i, F1 = ti, E2 = 1 + (b − 1)i e F2 = (b − 1) + i. Esta região tem
exatamente 2b − 1 pontos e, seguindo passos similares para o caso anterior, é fácil
ver que eles não todos classes diferentes módulo α.
Com o Teorema 2.4, vericamos que para o caso
tabela de pesos
s
s
∆α (s)
N
par e
a<b
temos a seguinte
e o número de vértices com esse peso, denotado por
0 1 2 ···
1 4 8 ···
t
t+1
2(b − 1) 4(b − t + 1)
···
···
b−1 b
4
1
Tabela 2.2: Distribuição de pesos no caso par com
Utilizando também o Teorema 2.4, para o caso
N
par e
∆α (s):
a<b
0 < a = b,
temos a
seguinte tabela:
s
0 1
∆α (s) 1 4
2 ···
8 ···
b−1
b
4b − 4 2b − 1
Tabela 2.3: Distribuição de pesos no caso par com
a=b
A seguir, considere como exemplo o grafo gaussiano gerado por α = 3 + 5i, cujo
2
2
número de vértices é N = 3 + 5 = 34. Nele, podemos aplicar o primeiro caso
(a < b) do Teorema 2.4 para determinar sua distribuição de distâncias. Note que
t = a+b
= 4. Assim, existem 1 vértice com peso 0, 4 (4 · 1) vértices com peso 1;
2
8 (4 · 2) vértices com peso 2; 12 (4 · 3) vértices com peso 3; 8 (2 · (5 − 1)) vértices com
peso 4; e 1 vértice com peso 5(b).
Corolário 2.1 Seja 0 6= α = a + bi ∈ Z[i] tal que 0 ≤ a ≤ b. Considere N = a2 + b2
a norma de α. O diâmetro k do grafo gaussiano Ga+bi é dado por: k = b se N é
par ou k = b − 1 se N é ímpar.
2.3
Grafos Circulantes e Gaussianos
34
Dem.: Pela Denição 2.6, o diâmetro k de G é o tamanho do maior entre todos
os menores caminhos de cada par de vértices possíveis do grafo. Além disso, Ga+bi
é vértice-simétrico. Dessa forma podemos xar um ponto qualquer e calcular qual é
o maior de todos os caminhos mais curtos entre um outro vértice e o xado. Este
será o diâmetro de Ga+bi . Por conveniência, xamos o vértice 0, pois sua distância
a um outro vértice v qualquer será Dα (0, v), ou seja, o peso de v , que é denotado
por ωα (v). Observando os Teoremas 2.3 e 2.4, notamos que o maior peso para o
caso N par é b e o maior peso para o caso em que N é ímpar será dado por b − 1.
Corolário 2.2 Seja 0 6= α = a + bi ∈ Z[i] tal que 0 ≤ a ≤ b. Considere N = a2 + b2
a norma de α. Então a distância média k do grafo gaussiano Gα é k =
2 −1)
se N é par ou k = 3b(N −1)+2a(a
se N é ímpar.
6(N −1)
Dem.:
a distânciaPmédia será dada por:
P Para o caso N ímpar,
P
u∈V,u6=u0
k=
Dα (u,u0 )
]V −1
Dα (u,0)
]V −1
u∈V,u6=0
=
=
3bN +2a(a2 −1)
6(N −1)
ωα (u)
N −1
06=u∈V
Vamos calcular separadamente o numerador dessa fração. Ele pode ser obtido
através do Teorema 2.3:
P
4(b − s)s
4s2 + b−1
Pb−1
Pt 2 t+1
= 4( 1 s + t+1 (b − s)s)
Pb−1 2
P
P
s
−
= 4( t1 s2 + b b−1
t+1 s )
t+1
t(t+1)(2t+1)
(b−1)(b−1+1)
= 4(
+ b(
− t(t+1)
) − ( (b−1)(b)(2b−2+1)
−
6
2
2
6
8 3
4
2
2 3
2
= 3 t + (4 − 2b)t + ( 3 − 2b)t − 3 b + 3 b
Pt
1
Substituindo t por
a+b−1
2
, temos:
8 a+b−1 3
( 2 ) + (4 − 2b)( a+b−1
)2
3
2
3
3
a
+ b2 − a3 + 12 a2 b − 12 b
3
3
2a +3b3 −2a+3a2 b−3b
6
3b(a2 +b2 −1)+2a(a2−1)
6
3b(N −1)+2a(a2−1)
6
Portanto, k =
t(t+1)(2t+1)
))
6
+ ( 43 − 2b)( a+b−1
) − 23 b + 23 b3
2
3b(N −1)+2a(a2 −1)
6(N −1)
Para
o caso N par, com a < b, a distância média será dada por:
P
ωα (u)
N −1
06=u∈V
Calculando separadamente o numerador da fração acima, através dos dados do
Teorema 2.4, ele é dado por:
Pt−1
1
4s2 + 2(b − 1)t +
Pb−1
t+1
4(b − s)s + b
2.3
Grafos Circulantes e Gaussianos
35
P
P
Pb−1 2
4 1t−1 s2 + 4b b−1
t+1 s − 4
t+1 s + 2(b − 1)t + b
(b−1)b
t(t+1)
(t−1)(t)(2t−2+1)
+4b( 2 − 2 )−4( (b−1)(b−1+1)(2b−2+1)
− t(t+1)(2t+1)
)+2bt−2t+b
4
6
6
6
Simplicando, obtemos:
8 3
t
3
− 2bt2 − 32 t + 13 b + 23 b3
:
Substituindo t por
a+b
2
8 a+b 3
( 2 ) − 2b( a+b
)2
3
2
3
3
2
− a3 + a3 + b2 + a2 b
−2a+2a3 +3b2 +3a2 b
6
3b(a2 +b2 )+2a(a2 −1)
6
3bN +2a(a2 −1)
6
− 23 ( a+b
) + 31 b + 23 b3
2
Portanto, k =
3bN +2a(a2 −1)
6(N −1)
.
Finalmente,
para o caso N par, com 0 < a = b, a distância média será dada por:
P
ωα (u)
N −1
06=u∈V
Calculando separadamente o numerador da fração acima, através dos dados do
Teorema 2.4, ele é dado por:
Pb−1 2
4s + (2b − 1)b
1
P
b−1 2
4 1 s + 2b2 − b
4 (b−1)(b)(2b−1)
+ 2b2 − b
6
4 3
1
−3b + 3b
Como neste caso b = t, podemos substituir b por
+ 43 ( a+b
)3
− 13 a+b
2
2
Portanto, k =
3bN +2a(a2 −1)
6(N −1)
a+b
2
.
.
Capítulo 3
O problema do caminho mais curto
Neste capítulo, consideramos o problema do caminho mais curto e explicamos como
resolvê-lo para as classe dos grafos Circulantes e Gaussianos, dando um simples algoritmo de roteamento, ou seja, um algoritmo que, a partir de um par de vértices,
roteia uma mensagem do vértice fonte para o vértice destino.
Sendo
u
e
v
dois vértices do grafo conexo
G,
o caminho mais curto entre
é uma sequência de arestas que, passando por vértices distintos, liga
u
e
v
u
e
v
de for-
ma a acumular o menor comprimento, ou distância. Trata-se de um dos problemas
mais conhecidos e antigos da humanidade e como solução destaca-se o Algoritmo
de Dijkstra (1959), ilustrado a seguir, que, apesar de ter uma fácil implementação
computacional e de calcular as menores distâncias de um vértice inicial a todos os
outros apenas com a restrição de que não haja arcos negativos no grafo, sua ordem
2
de complexidade é O(n ). Portanto, o custo computacional desse algoritmo, que
pode ser utilizado em um grafo qualquer, pode ser muito alto. Mas como as classes
de grafos que são objetos de estudo deste trabalho têm uma estrutura especíca,
algoritmos podem ser implementados aproveitando suas peculiaridades.
3.1
Algoritmo de Dijkstra
Em 1959, Dijsktra sugeriu um algoritmo de rotulação para caminhos em grafos
com arcos positivos utilizando indução e ajuste, eciente e de fácil implementação
computacional. Chamando de:
•
Lista
F
(lista dos nós fechados): conjunto dos vértices para o qual já se conhece
um caminho mínimo
•
Lista
A
(lista de nós abertos):
conjunto dos nós para o qual ainda não se
conhece um caminho mínimo
• i:
contador de iterações
• V:
• r:
representando o conjunto os nós rotulados e abertos em
índice do vértice a ser fechado na iteração t
36
G
3.2
O problema do caminho mais curto
• C = [Cij ] :
37
matriz dos custos representando as distâncias entre vértices ligados
diretamente
• dij :
a distância entre os vértice
• dtij :
a distância calculada entre os vértices
• rot(i):
e
xj
xi
e
xj
na iteração
t
vetor que guarda o vértice que deu origem à distância calculada para
o vértice de índice
• Γ+ (r)
xi
i
: conjunto de vizinhos do vértice de índice
r
Podemos escrever o algoritmo como segue:
Algoritmo de Dijkstra (Caminho mais Curto)
INÍCIO
Ler os dados de
G = (N, d),
onde
dij
é a distância entre os nós vizinhos de G
d11 ← 0;
{d1i ← ∞, ∀i ∈ N − {x1 }} ;
V ← {x1 };
A ← {N };
F ← ∅;
{rot(i) ← 0, ∀i ∈ N }
Para t = 1 a n fazer
{d1j }
r ← xi tal que d1i ← xmin
i ∈A
F ← F ∪ {r};
A ← A − {r};
V ← A ∩ Γ+ (r)
Para i ∈ V fazer
t−1
p ← min{d1i
, (d1r + dr1 )}
t−1
Se p < d1i , então
t−1
d1i
← p;
rot(i) ← r;
Fim
Fim
Fim
FIM
Observe que para cada vértice
para aproximar a distância
v
até
u em V é
u em G.
denido um rótulo
comprimento do melhor caminho encontrado até o momento de
d11 = 0
e
D1i = ∞,
para cada
u 6= v
e denimos o conjunto
que será usado
F
v até u.
Inicialmente,
inicialmente vazio. A
F com o menor
rótulo dij e coloca-se em F . Na primeira iteração, F conterá apenas v . Quando um
novo vértice entra em F , são atualizados todos os rótulos dij , em que z é um vértice
adjacente a u e não está em F , reetindo o fato de que pode haver uma nova e melhor
maneira de chegar a z via u. Esta atualização é conhecida como relaxamento, que
em Djkstra é feito para uma aresta (u, z) de forma que se calcula um novo valor para
D[u] e deseja-se vericar se há um valor melhor para D[z] usando a aresta (u, z).
cada iteração, seleciona-se um vértice
u
dij ,
Estes rótulos armazenarão sempre o
que não está no conjunto
3.2
O problema do caminho mais curto
3.2
38
Roteamento em Grafos Circulantes
Ao longo dos anos, muitos esforços foram feitos para se obter algoritmos ótimos que
encontrem caminhos mínimos em grafos circulantes. Tais algoritmos consideram grafos cujos vértices são rotulados por inteiros. Se
CN (j1 , j2 ), um caminho mais
|y| saltos em j2 , onde x, y ∈ Z.
circulante
em
j1
e
n, m ∈ ZN são dois vértices do grafo
n para m consistirá em |x| saltos
curto de
Consequentemente, todos estes algoritmos
de roteamento podem ter um passo de pré-processamento comum
Calcular(x, y).
Por conseguinte, um algoritmo de roteamento genérico poderia ser como o descrito
no Algoritmo 1. Ele faz o cálculo do caminho mais curto em grafos circulantes de
grau quatro e foi apresentado por Robic (1996)
apud
Martínez (2007).
entrada: X,Y
saída: m,n
início
PASSO 1. CALCULE(X, Y);
PASSO 2. para i := 0 até |x| faça n = n + sign(x) j_1 (mod N);
PASSO 3. para i := 0 até |y| faça m := m + sign(y) j_2 (mod N);
fim Algoritmo 1:
No Passo 1, calcula-se o par
com
|x| + |y|
(x, y) ∈ Z × Z
tal que
n − m ≡ xj1 + yj2 (mod N )
mínimo.
Os Passos 2 e 3 tomam
|x| + |y| < k
saltos, onde
k
é o diâmetro do grafo. A
complexidade computacional deste algoritmo é da ordem de complexidade do Passo
1 mais
O(k).
Por essa razão, a maioria dos artigos sobre roteamento em grafos cir-
culantes focalizam em algoritmos para resolver o Passo 1, com o objetivo de reduzir
seu custo de roteamento.
3.2.1
Programa para Roteamento em Grafos Circulantes
Na Figura 3.1, temos um exemplo de um grafo circulante com dois saltos. Ele foi
desenvolvido baseado no fato que os
N
vértices podem ser representados sobre um
cos(i ∗ arg), sen(i ∗ arg) para as
i varia de 0 a N − 1 e arg = (2 ∗ pi)/N . As arestas
círculo, igualmente espaçados, usando as fórmulas
coordenadas de cada ponto, onde
são calculadas conforme a Denição 2.10 de grafos circulantes.
3.2
O problema do caminho mais curto
39
Figura 3.1: Grafo Circulante com 18 vértices e saltos 3 e 5
Apresentamos os resultados do algoritmo que trata do roteamento em um grafo
circulante. Para exemplicar, considere o caso em que temos o grafo
C18 (3, 5),
ou
seja, um grafo circulante com 18 vértices e saltos 3 e 5. Nele, queremos encontrar
o menor caminho que vai do vértice 1 ao vértice 12. Na saída do programa, obtemos como resultado, que o caminho deve ser feito pelo vetor
[+1 − 2],
que signica
caminhar, a partir do vértice 1, 1 passo no sentido anti-horário com o salto 3 e 2
passos no sentido horário com o salto 5. Na ilustração da Figura 3.2, gerada pelo
programa, vemos o caminho descrito acima. O passo dado com o salto 3 está mostrado pela linha tracejada e os passos dados com salto 5 estão mostrados pela linha
contínua.
Figura 3.2: Menor caminho entre os vértices 1 e 12 do Grafo Circulante
C18 (3, 5)
O programa, desenvolvido para o roteamento em grafos circulantes quaisquer,
possui como parâmetros de entrada, as seguintes variáveis:
3.2
O problema do caminho mais curto
• N:
40
número de vértices do grafo circulante
• A, B :
saltos do grafo circulante
• m, n:
vértices do grafo nos quais será feita a busca do menor caminho entre
eles
Durante sua execução, ele tem como objetivo determinar menor caminho entre os
m, n ∈ ZN , indo de m a n. Para isso, deve-se resolver a equação diofantina:
xA + yB = m − n + kN , com |x| + |y| mínimo e k inteiro.
Primeiramente, o programa verica se n > m ou m > n. Caso aconteça a
segunda opção, as variáveis são trocadas, a m de se manter em n o vértice com
vértices
maior valor.
Em seguida, escolhe o melhor sentido para busca (horário ou anti-
horário) vericando o quão próximos estão os vértices
m, n.
Isso se justica, pois a
disposição dos mesmos é feita de forma circular. Assim, num grafo circulante de 15
vértices, por exemplo, os vértices 1 e 14 estão mais próximos do que 1 e 6. Assim,
se
n − m > N − (n − m),
tomamos
c = n − m − N,
n−m
c = n − m e,
indicando que o sinal de
será trocado, pois o sentido de busca será horário.
Caso contrário,
dessa forma, o sinal permanece, porque o sentido da busca será anti-horário.
Então executa-se um algoritmo auxiliar (Euclides Estendido), baseado nos re-
Ax0 + By0 = 1, a partir dos
parâmetros A e B , o que retornará um vetor euc = [x0 y0 mdc(A, B)].
Depois disso, é chamada uma outra rotina que calcula X, Y tais que AX + BY =
c, com |X| + |Y | mínimo e c sendo um número inteiro da forma kN + (m − n). Tal
sultados do Capítulo 2, que calcula
x0
e
y0
tais que
rotina baseia-se em um resultado importante da álgebra abstrata, que aproveita da
estrutura de equação diofantina do problema para resolvê-lo. Ele diz que se tiver-
a, b e c inteiros tais que d = mdc(a, b) divide c, então escrevendo d na forma
d = ra + sb, com r; s ∈ Z, temos que as soluções da equação diofantina são da forma
x = r dc + db t; y = s dc − ad t, com t ∈ Z.
c
b
c
a
Observe que devemos minimizar a função inteira f (t) = |r + t|+|s − t|, t ∈ Z.
d
d
d
d
c
b
c
a
Considere então g(t) = r + t e h(t) = s − t, que são funções lineares. Se
d
d
d
d
tomarmos as funções |g(t)| e |h(t)|, supondo a variável t real, simultaneamente no
mos
mesmo gráco, teremos um esboço como o da gura 3.3:
Figura 3.3: Gráco das funções
|g|
e
|h|
Evidentemente, as inclinações podem variar, assim como as posições das funções
0
no gráco. Mas o importante é notar que entre r e r haverá uma interseção I , fácil
3.3
O problema do caminho mais curto
41
de ser obtida algebricamente, que será o mínimo para a soma
Observe que as funções
f
e
|g(t)| + |h(t)|
|g(t)| + |h(t)|, t ∈ R.
possuem a mesma expressão algébrica.
Entretanto, na primeira, a variável é inteira, enquanto na segunda a variável é real.
t0 do valor real I , assim como o
|X| + |Y | = |r dc + db t| + |s dc − ad t|
Dessa forma, o programa considera o menor inteiro
maior inteiro de
I
como parâmetros na solução de
mínimo, vericando qual dos dois é menor.
X, Y calculados, o programa verica qual k é o melhor de tal forc = kN + (m − n) gere o melhor par X, Y . Ao variar k , temos números
congruentes módulo N . Após esse passo, o algoritmo busca a melhor solução entre
A partir de
ma que
as dez calculadas e, a partir dela, faz uma ilustração do menor caminho no grafo
circulante, indicando com cada cor, o salto utilizado.
O programa ainda gera na sua saída uma matriz
uma solução para o problema.
necessários para
A
w,
onde cada linha apresenta
Na primeira coluna, temos o número de saltos
e, na segunda, para o
B.
Em ambos, se o número for posi-
tivo, a rotação é no sentindo anti-horário e se for negativo, a rotação é no sentindo
w, aparece o número total de saltos a serem utilizados
z , também exibida na saída, indica a linha da matriz w
horário. Na terceira coluna de
no roteamento. A variável
com solução mais eciente.
Os códigos-fontes das funções auxiliares utilizadas nesse programa estão no anexo
1, na seção de roteamento de grafos circulantes.
3.3
Roteamento em Grafos Gaussianos
Como em grafos circulantes de grau quatro, se quisermos achar o caminho de um
0
vértice fonte η para um vértice destino η em um grafo Gaussiano, teremos que calcu0
lar r = r1 + ir2 ≡ η − η (mod α) com |r1 | + |r2 | mínimo. Então qualquer combinação
de
r1
saltos na dimensão real e
r2
saltos na dimensão imaginária nos dará uma li0
gação de caminho mais curto entre o vértice de fonte η e o vértice destino η . Um
algoritmo de roteamento semelhante ao apresentado no Algoritmo 1 também pode
ser usado em grafos Gaussianos.
r = r1 + r2 i com |r1 | + |r2 | mínimo.
Martínez (2007) propõe um algoritmo que acha
Este algoritmo está baseado no próximo teorema
e tira vantagem da rotulação dos vértices em termos de inteiros Gaussianos.
Teorema 3.1 Seja 0 6= α = a + bi ∈ Z[i] e k o diâmetro de Gα . Sejam η = x + yi
e η 0 = x0 + y 0 i tais que |x| + |y| ≤ k e |x0 | + |y 0 | ≤ k . Se r ≡ (η 0 − η) (mod α) é tal
que |Re(r)| + |Im(r)| é mínima, então r = (η 0 − η) + γα com γ ∈ {0, ±1, ±i, ±(1 +
i), ±(1 − i), ±2, ±2i}.
Dem.: Usaremos a distribuição de distâncias introduzida nos Teoremas 2.3 e
2.4. De acordo com o Teorema 2.3, se N = a2 + b2 é ímpar, a norma máxima é
+ b−a−1
i ou qualquer um de seus associados. Logo,
obtida para o vértice δ = a+b−1
2
2
2
2
temos que N (δ) = ( a+b−1
)2 + ( b−a−1
)2 = a +(b−1)
.
2
2
2
Agora, dados η = x+yi e η 0 = x0 +y 0 i, como r = (η 0 −η)+αγ com |Re(r)|+|Im(r)|
mínimo, obtemos que γα = r − (η 0 − η). Aplicando a norma em ambos os lados da
2
2
iguadade, obtemos: N (γα) = N (r − (η 0 − η)) ≤ N (3δ) = 9 a +(b−1)
.
2
3.3
O problema do caminho mais curto
42
Por outro lado, N (γα) = N (γ)N (α). Então N (γ) = NN(γα)
. Como N (α) =
(α)
2 +(b−1)2
a
a2 + b2 , concluímos que N (γ) ≤ 92 a2 +b2 < 92 . Os únicos valores possíveis de
γ que satisfazem a desigualdade são {0, ±1, ±i, ±(1 + i), ±(1 − i), ±2, ±2i}. Se
+ b−a
i. Temos que
N é par, a norma máxima é alcançada pelo vértice δ = a+b
2
2
2
2
a+b 2
b−a 2
a +b
N (δ) = ( 2 ) + ( 2 ) = 2 . Assim, com passos análogos ao primeiro passo,
obtemos as mesmas restrições para a norma de γ .
Desta forma, com base no Teorema 3.1, o algoritmo a seguir apresenta uma
versão paralela do cálculo de distância mais curta para qualquer Grafo Gaussiano.
Dados: x + yi: Fonte; x' + y'i: Destino; a + bi: grafo gerador
Resultado: r_1+r_2 i
mínimo
(x_0-x)+(y_0-y)i (mod a+bi): com |r_1|+|r_2|
início
x_0 := x' - x; y_0 := y' - y;
FAÇA EM PARALELO:
x_1 := x_0 - a; y_1 := y_0 - b;
x_2 := x_0 + a; y_2 := y_0 + b;
x_3 := x_0 - b; y_3 := y_0 + a;
x_4 := x_0 + b; y_4 := y_0 - a;
x_5 := x_0 + (a - b); y_5 := y_0 + (a + b);
x_6 := x_0 - (a - b); y_6 := y_0 - (a + b);
x_7 := x_0 + (a + b); y_7 := y_0 + (b - a);
x_8 := x_0 - (a + b); y_8 := y_0 - (b - a);
x_9 := x_0 + 2a; y9 := y_0 + 2b;
x_1 0 := x_0 - 2a; y10 := y_0-2b
x_{11} := x_0 - 2b; y_{11} := y_0 + 2a;
x_{12} := x_0 + 2b; y_{12} := y_0 - 2a;
FIM DO FAZER EM PARALELO
(r_1, r_2) := (x_i, y_i) tal que |x_i| + |y_i| é mínimo;
fim
Note que no Algoritmo 2 são necessárias apenas somas e comparações para o
0
0
roteamento em grafos Gaussianos. O vértice fonte x + yi e o vértice destino x + y i
3.3
O problema do caminho mais curto
são tais que
|x| + |y| ≤ k
e
|x0 | + |y 0 | ≤ k ,
43
onde
k
é o diâmetro do grafo Gaussiano.
Observe que, para obter o diâmetro, precisamos apenas vericar a paridade de N =
a2 + b2 . Portanto, o FAÇA EM PARALELO no Algoritmo 2 substitui o Passo 1
(Calcular(x, y )) do Algoritmo 1, que é a parte mais cara do processo, usando apenas
12
somas e
14
comparações. Portanto, nesse processo de roteamento, existe a
vantagem de existir uma computação em paralelo, o que reduz signicativamente o
custo computacional.
3.3.1
Programa para Roteamento em Grafos Gaussianos
Na Figura 3.4, temos um Grafo Gaussiano gerado pelo elemento 5 + 8i. Como desN = 52 + 82 = 89 vértices, dispostos de forma que 25
crito anteriormente, ele possui
deles são representados em um quadrado de lado 5 e os 64 restantes em um outro
quadrado de lado 8. Os dois quadrados são justapostos, sendo que o de menor lado
ca à esquerda.
Figura 3.4: Grafo Gaussiano gerado por
5 + 8i
Na Figura 3.5, ilustramos o grafo correspondente ao da Figura 3.4, cujo gerador
é o elemento
5 + 8i.
3.3
O problema do caminho mais curto
44
Figura 3.5: Grafo Gaussiano gerado por
5 + 8i
na topologia losangular
Para o problema de encontrar o menor caminho entre dois vértices de um grafo Gaussiano, foi implementado um programa baseado no Teorema 3.1.
que queremos encontrar o menor caminho entre os vértices
Gaussiano gerado por
5 + 3i
e
7 + 0i
Suponha
do grafo
3+5i. Então o programa dispõe os vértices do grafo Gaussiano
na topologia losangular, de forma que cada vértice dessa topologia representa um
vértice da antiga de tal forma que estão na mesma classe de equivalência e que o
vértice do novo grafo seja o de menor norma possível dentre todos os existentes na
classe.
Evidentemente, essa transformação afeta os vértices
na topologia losangular são
−1 − 2i
e
2 − 2i
5 + 3i
e
7 + 0i,
que
As adjacências são preservadas, o que
garante ao novo grafo ser isomorfo ao anterior. Ao executar o programa, é gerada
em sua saída uma ilustração com um dos menores caminhos (pode existir mais de
um) entre o vértice de origem e o vértice de destino como mostrado na Figura 3.6.
Figura 3.6: Menor caminho entre os vértices 5+3i e 7+0i do grafo gaussiano
G3+5i
3.3
O problema do caminho mais curto
45
O mesmo caminho é ilustrado na Figura 3.7, através da topologia em L.
Podemos concluir que o cálculo da distância mínima em grafos circulantes tem
um custo maior do que em grafos Gaussianos, sendo, dessa forma, vantajosa a utilização do último quando for possível encontrar um isomorfo ao grafo circulante em
questão.
No Anexo 1 estão presentes os códigos-fontes de cada função auxiliar utilizada
no programa para o roteamento em grafos Gaussianos.
Figura 3.7: Menor caminho entre os vértices 5+3i e 7+0i do grafo gaussiano
na topologia em L
G3+5i
Capítulo 4
O problema das árvores geradoras
independentes
Neste capítulo, trabalhamos com o conceito de árvores geradoras independentes. A
construção das mesmas em grafos de forma geral é signicante para aplicações em
redes. No caso de grafos circulantes recursivos, uma subclasse dos grafos circulantes
que deniremos neste capítulo, dentre outras aplicações, tais árvores desempenham
papel fundamental na distribuição de mensagens secretas, por exemplo.
4.1
Árvores Geradoras Independentes (IST)
Para um grafo não-direcionado
G,
considere
P e Q unindo x e y são ditos internamente
E(P ) ∩ E(Q) = ∅ e V (P ) ∩ V (Q) = {x, y}.
minhos
se
x, y ∈ V (G).
Dizemos que dois ca-
disjuntos, denotados por
P ||Q,
Exemplo 4.1 No grafo a seguir, os caminhos P : 0 1 2 7 6 e Q : 0 3 5 6 conectam os
vértices x = 0 e y = 6 e são disjuntos, pois E(P )∩E(Q) = ∅ e V (P )∩V (Q) = {0, 6}.
Por outro lado, os caminhos P : 0 1 2 7 6 e R : 0 3 7 6 não são disjuntos, já que
V (P ) ∩ V (R) = {0, 7, 6}.
Figura 4.1: Exemplo de caminhos disjuntos
46
4.1
O problema das árvores geradoras independentes
47
Denição 4.1 Uma árvore geradora enraizada T de um grafo G é um subgrafo de
G que contém todos os vértices V (G) = V (T ) sem formar ciclos e possui um vértice
especíco como sua raiz.
Exemplo 4.2 Considerando o grafo G do Exemplo 4.1, as árvores seguintes são
árvores geradoras enraizadas no vértice 0.
Figura 4.2: Árvores Geradoras
x, y ∈ V (T ), denotamos por T [x, y] o único caminho de x a y
T e T 0 de um grafo G são ditas independentes (IST) se
0
são enraizadas no mesmo vértice, digamos r , e são tais que T [r, x]||T [r, x] para todo
x 6= r. Observe que no Exemplo 4.2 temos duas árvores geradoras independentes.
em
Se
T
T.
Duas árvores geradoras
é uma árvore e
Dizemos também que um conjunto de árvores geradoras é independente se elas são
duas a duas independentes.
C(N, d), os quais são uma classe especial de grafos circulantes, que possuem um número N de vértices e, como saltos,
potências de um inteiro d, de 0 até dlogd N e − 1. Assim, podemos escrever esses
0 1 2
dlogd N e−1
grafos da seguinte forma C(N, d) = CN (d , d , d , . . . , d
) e os vértices serão
rotulados de 0 a N − 1.
m
Grafos C(N, d) têm uma estrutura recursiva quando N = cd , 1 ≤ c < d e m > 1
Neste capítulo, trabalharemos com os grafos
e são chamados grafos circulantes recursivos ou RC-grafos. Isso signica que um
m
grafo C(cd , d) pode ser denido recursivamente utilizando a seguinte propriedade:
Proposição 4.1 Seja Vi um subconjunto de vértices de G = C(cdm , d) tal que Vi =
{v|v ≡ i (mod d)}, m ≥ 1. Então
(i) Para 0 ≤ i < d, o subgrafo de G(cdm , d) induzido por Vi é isomorfo a
G(cdm−1 , d).
(ii) G pode ser particionado em d subgrafos disjuntos Gi (Vi , Ei )
Dem.:
i) Considere, para cada i, com 0 < i < d, Gi = Gi (Vi , Ei ), o subgrafo de
C(cdm , d) induzido por Vi . Vamos mostrar que Gi ∼
= C(cdm−1 , d). Note que |Vi | =
cdm−1 e que Vi = {i+dj|0 ≤ j ≤ cdm−1 −1}. De fato, se v ∈ Vi , então v = i+dj, t ∈ Z
e 0 ≤ v ≤ cdm − 1. Como 0 ≤ i ≤ d − 1, temos 0 ≤ v − i ≤ v ≤ cdm − 1, o que
m
≤ b cd d−1 c ≤ cdm−1 − 1. Agora, considere a seguinte função:
implica 0 ≤ t = v−i
d
4.1
O problema das árvores geradoras independentes
48
Gi
→ C(cdm−1 , d)
i + dj 7→
j
Claramente, ϕ é bijetora. Seja (i + dk, i + dl) ∈ Ei , k 6= l. Então existe t, com
0 ≤ t ≤ dlogd N e, tal que (i + dk) − (i + dl) ≡ dt (mod cdm ), ou seja, d(k − l) ≡
dt (mod cdm ). Logo, k − l ≡ dt−1 (mod cdm−1 ), o que implica (k, l) ∈ E(C(cdm−1 , d)).
Portanto, Gi ∼
= C(cdm−1 , d).
ii) Para quaisquer i, k ∈ {0, . . . , d − 1}, i 6= j, temos Vi ∩ Vj = ∅. De fato, se
tívessemos v ∈ Vi ∩ Vj , então teríamos v = i + dk = j + dl, ou seja, i − j ≡ 0 (mod d),
o que implicaria em i = j .
Armação V (G) = ∪˙ 0≤i≤d Vi .
˙ i ⊆ G. Seja x ∈ G. Se x < d, então x ∈ Vx . Suponha que
Obviamente, ∪V
m
d ≤ x < N = cd . Então x =Sdk + r, 0 ≤ r < d, com 0 ≤ k ≤ cdm−1 − 1. Portanto,
x ∈ Vr . Além disso, E(G) = 0≤i<d Ei ∪ X , onde X = {(v, w), u, w ∈ V (G)|v ± 1 ≡
w (mod cdm )}.
De fato, se (v, w) ∈ E(G), então v −w = dt (mod cdm ), com 0 ≤ t ≤ dlogd N e−1.
Se t = 0, então v − w = 1 (mod cdm ). Logo, (v, w) ∈ X . Suponha t > 0. Assim,
v − w = dt + cdm s, s ∈ Z. Consequentemente, v − w = d(dt−1 + cdm−1 s), s ∈ Z.
Tome v, w ∈ V (G) = ∪0≤i≤d Vi . Se v, w ∈ Vi , então, como Gi é um subgrafo
induzido de G, temos (v, w) ∈ Ei e o resultado segue. Por outro lado, Se v ∈ Vi
e w ∈ Vj , com i 6= j , então v = i + dk e w = j + dl, o que implica v − w =
i − j + d(k − l) = d(dt−1 + cdm−1 . Portanto, i − j ≡ 0 (mod d), o que não é possível,
pois 0 ≤ i, j < d e i 6= j .
ϕ:
Exemplo 4.3 Considere o grafo circulante recursivo C(18, 3), onde c = 2, d = 3 e
m = 2. Seus saltos serão 30 , 31 , 32 , pois dlog3 18e − 1 = 2. Sua ilustração pode ser
vista na Figura 4.1:
Figura 4.3: Grafo circulante recursivo
C(18, 3)
4.1
O problema das árvores geradoras independentes
49
Conforme vimos, o grafo C(18, 3) pode ser particionado em três cópias de C(6, 3),
G0 (V0 , E0 ), G0 (V1 , E1 ), G2 (V2 , E2 ), nos quais os conjuntos de vértices são dados por
Vi = {j|j ≡ i (mod 3)}, onde i varia entre 0 e 2, ou seja, V0 = {0, 3, 6, 9, 12, 15}, V1 =
{1, 4, 7, 10, 13, 16} e V2 = {2, 5, 8, 11, 14, 17}. Cada um desses subgrafos está ilustrado
em uma cor na Figura 4.2.
Figura 4.4: Grafo circulante recursivo
C(18, 3)
C(cdm , d) pode ser visto como sendo um grafo de
ZN com o conjunto gerador {d0 , d1 , . . . , ddlogd N e−1 },
O grafo
po cíclico
k -ésimo
Cayley sobre o gruk
onde d é chamado
É bem conhecido que cada grafo de Cayley sobre um grupo geral
m
é vértice-simétrico e, portanto, é regular. Denotemos por δm o grau de C(cd , d).
m−1
Assim, δm−1 é o grau de cada vértice i no subgrafo C(cd
, d) e δm é o grau de cada
m
vértice j no grafo C(cd , d). Provaremos a seguir que δm = δm−1 + 2 para m ≥ 1.
m
Tome j ∈ C(cd , d). Então j ∈ Vi , para algum i ∈ {0, 1, 2, . . .}. Portanto,
j ≡ i (mod d). Note que cada j ± dt , com t ∈ {1, 2, . . . , dlogd N e − 1}, é adjacente ao
vértice
salto.
j.
Além disso,
j + dt ≡ i (mod d),
pois
dt ≡ 0 (mod d)
j±1
e
j ≡ i (mod d).
Por outro
não estão na mesma classe de equivalência que i, já que i ≡ j (mod d).
t
Portanto, j + d ∈ Vi , j − 1 ∈
/ Vi e j + 1 ∈
/ Vi . Assim sendo, o vértice j
m−1
de C(cd
, d) possui dois vértices adjacentes a menos que em C(cdm , d), o que é
lado,
suciente para mostrar a igualdade
δm = δm−1 + 2.
4.1
O problema das árvores geradoras independentes
Figura 4.5: Vértices adjacentes a
j
no grafo
50
C(cdm−1 , d)
Proposição 4.2 Para um grafo circulante recursivo C(cdm , d), δm é dado da se-
guinte forma:

2m - 1, se c = 1 e d = 2



2m,
se c = 1 e d > 2
δm =
2m + 1, se c = 2;



2m + 2, se c > 2
Dem.: Pela denição, grafos circulantes recursivos C(cdm , d) têm saltos dados pelo conjunto {d0 , d1 , d2 , . . . , ddlogd N e−1 }, onde N = cdm . Vamos considerar os
seguintes casos:
• c=1ed=2
Neste caso, dlogd N e = dlog2 2m e = dme = m, o que nos dá o conjunto de
saltos: {d0 , d1 , d2 , . . . , dm−1 }. Então os vértices adjacentes ao vértice rotulado
como x são x ± 20 , x ± 21 , x ± 22 , . . . , x ± 2m−1 . Mas os vértices x + 2m−1
e x − 2m−1 são os mesmos. De fato, as contas são tomadas módulo N que,
neste caso, é N = 2m . Observe que 2m ≡ 0 (mod 2m ) e, assim, 2 · 2m−1 ≡
0 (mod 2m ), ou seja, 2m−1 +2m−1 ≡ 0 (mod 2m ). Logo, 2m−1 ≡ −2m−1 (mod 2m )
e, consequentemente, x + 2m−1 ≡ x − 2m−1 (mod 2m ). Além disso, os vértices
x+2t e x−2t , com t < m−1, não são congruentes módulo 2m , pois, se fossem,
teríamos 2t ≡ −2t (mod 2m ), ou ainda, 2·2t ≡ 0 (mod 2m ), o que não é verdade,
já que 21+t < 2m . De forma análoga, a igualdade entre elementos x+2t e x+2q ,
com t < q , também não seria possível, pois como 0 < 2t − 2q < 2m , então
2t − 2q não é congruente a 0 módulo 2m e, assim, não pode ocorrer x + 2t ≡
x + 2q (mod 2m ). O mesmo raciocínio é válido para as demais comparações
entre x ± 2t e x ± 2q , com q 6= t. Portanto, existem 2m − 1 vértices adjacentes
a cada vértice x do grafo, ou seja, δm = 2m − 1.
• c=1 e d>2
Nessas condições, o conjunto de saltos é dado por {d0 , d1 , d2 , . . . , dm−1 }, pois
dlogd N e = dlogd dm e = dme = m. Considerando que d > 0, dado um vértice x,
os seguintes vértices são adjacentes a ele: x ± d0 , x ± d1 , x ± d2 , . . . , x ± dm−1 .
Neste caso, os vértices x+dt e x−dt , com 0 ≤ t ≤ m−1 são distintos, pois caso
4.1
O problema das árvores geradoras independentes
51
ocorresse x + dt ≡ x − dt (mod dm ), então teríamos 2 · dt ≡ 0 (mod dm ), o que
não é verdade já que 0 < 2 · dt < d · dm−1 = dm (estamos considerando d > 2).
De forma análoga, a igualdade entre elementos x + dt e x + dq , com t < q ,
também não seria possível, pois como 0 < dt − dq < dm , então dt − dq não é
congruente a 0 módulo dm e, assim, não pode ocorrer x + dt ≡ x + dq (mod dm ).
O mesmo raciocínio é válido para as demais comparações entre x ± dt e x ± dq ,
com q 6= t. Portanto, existem 2m vértices adjacentes a cada vértice x do grafo,
ou seja, δm = 2m.
• c=2
Neste caso, dlogd N e = dlogd 2 · dm e = dlogd 2 + logd dm e = dlogd 2 + me = m + 1,
pois 0 < logd 2 < 1. Isto nos dá o conjunto de saltos: {d0 , d1 , d2 , . . . , dm }.
Então os vértices adjacentes ao vértice rotulado como x são x ± d0 , x ± d1 , x ±
d2 , . . . , x ± dm . Mas os vértices x + dm e x − dm são os mesmos. De fato,
as contas são tomadas módulo N que, neste caso, é N = 2 · dm . Observe
que 2 · dm ≡ 0 (mod 2 · dm ) e, assim, dm + dm ≡ 0 (mod 2 · dm ), ou seja,
dm ≡ −dm (mod 2 · dm ). Logo, x + dm ≡ x − dm (mod 2 · dm ). Além disso, os
vértices x + dt e x − dt , com t < m, não são congruentes módulo 2 · dm , pois,
se fossem, teríamos dt ≡ −dt (mod 2 · dm ), ou ainda, 2 · 2t ≡ 0 (mod 2 · dm ), o
que não é verdade já que 2 · dt = 21+t < 2 · dm . De forma análoga, a igualdade
entre elementos x + dt e x + dq , com t < q , também não seria possível, pois
como 0 < dt − dq < 2dm , então dt − dq não é congruente a 0 módulo 2 · dm e,
assim, não pode ocorrer x + dt ≡ x + dq (mod 2 · dm ). O mesmo raciocínio é
válido para as demais comparações entre x ± dt e x ± dq , com q 6= t. Portanto,
existem 2(m + 1) − 1 = 2m + 1 vértices adjacentes a cada vértice x do grafo,
ou seja, δm = 2m + 1.
• c>2
Nesta última condição, temos dlogd N e = dlogd c · dm e = dlogd c + logd dm e =
dlogd c + me = m + 1, pois, como c < d, então 0 < logd c < 1. Isto nos dá
o conjunto de saltos: {d0 , d1 , d2 , . . . , dm+1 }. Então os vértices adjacentes ao
vértice rotulado como x são x ± d0 , x ± d1 , x ± d2 , . . . , x ± dm+1 . Neste caso,
os vértices x + dt e x − dt , com 0 ≤ t ≤ m + 1 não são os mesmos. De fato,
as contas são tomadas módulo N que, neste caso, é N = c · dm . Observe que
se os vértices fossem iguais, teríamos x + dt ≡ x − dt (mod c · dm ), ou seja,
2 · dt ≡ 0 (mod c · dm ), o que não é verdade pois 0 < 2 · dt < c · dm . De forma
análoga, a igualdade entre elementos x + dt e x + dq , com t < q , também não
seria possível, pois como 0 < dt − dq < c · dm , então dt − dq não é congruente
a 0 módulo c · dm e, assim, não pode ocorrer x + dt ≡ x + dq (mod c · dm ). O
mesmo raciocínio é válido para as demais comparações entre x ± dt e x ± dq ,
com q 6= t. Portanto, existem 2(m + 1) = 2m + 2 vértices adjacentes a cada
vértice x do grafo, ou seja, δm = 2m + 2.
A vizinhança de um vértice
vértices adjacentes a
x
x,
denotada por
N (x),
é o conjunto de todos os
em um grafo. Como RC-Grafos são vértice-simétricos, sem
perda de generalidade, podemos simplesmente considerar o vértice 0 como raiz da
m
k
IST para C(cd , d). Obviamente, N (0) = {±d : 0 ≤ k ≤ dlogd N e − 1}.
4.1
O problema das árvores geradoras independentes
Seja
= = {T1 , T2 , . . . , Tn }
52
um conjunto constituído por n árvores geradoras inC(cdm , d). Veremos mais tarde que n = δm .
dependentes enraizadas em 0 no grafo
T ∈ =, o pai de um vértice x(6= 0), denotado por pai(T, x), é um vérm
tice adjacente a x no caminho T [x, 0]. Da conectividade de C(cd , d) e do fato de
|=| = δm , existe apenas um lho de 0 em cada árvore geradora T ∈ =. Assim,
k
k
k
se x = +d (respectivamente, x = −d ), então ele usa o salto j = −d (respectik
k
vamente, j = +d ) para conectar à raiz. Além disso, j = −d (respectivamente,
j = +dk ) é o último salto em um caminho ligando cada vértice e a raiz. Por isso,
−
+
denotamos por Tk (respectivamente, Tk ) para especicar a IST cuja raiz possui
k
k
+d (respectivamente,−d ) como seu lho. Por exemplo, quatro IST's enraizadas
em 0 no grafo C(16, 4) são mostradas na Figura 4.4.
Para cada
Figura 4.6: Árvores Geradoras Independentes no grafo
C(16, 4)
+dk
Para representar explicitamente a adjacência, usamos a notação x → y se x +
−dk
dk = y (respectivamente, x → y se x − dk = y ) para signicar que ambos os vértices
x, y ∈ C(cdm , d) são conectados pelo k -ésimo salto. Assim, podemos representar um
caminho usando esta notação repetidamente.
k
Seja J = {±d : 0 ≤ k ≤ dlogd N e − 1}. Se um salto j ∈ J ocorre sucessivamente
j
para conectar x e y , então usamos a notação x ⇒α y para dizer que y = x + α · j ,
m
onde α é o número de repetições de j entre x e y . Seja x(6= 0) ∈ C(cd , d) qualquer
j1−1
j1
j2
j3
jl
vértice e suponha que x0 → x1 → x2 → · · · → xl−1 → xl é um caminho mais
curto que liga
x(= x0 )
e
0(= xl ),
onde cada
ji ∈ J
é um salto. Por uma questão de
caminho
mais curto
P
de x e é denotado por Px .
l
Como x pode ser decomposto na soma
i=1 (−ji ), dizemos que uma decomposição
de x é a sua representação de seus termos pelos seus saltos. Para j ∈ J , denotamos
conveniência, tal caminho é chamado
por
n(Px , j)
o número de ocorrências de
j
em
Px .
Proposição 4.3 Para Px , um caminho mais curto entre x e 0, são válidas as se-
guintes condições:
(i) xi 6= xk para 0 ≤ i, k ≤ l e i 6= k ;
(ii) ji 6= −jk para 1 ≤ i, k ≤ l e i 6= k
(iii) n(Pk , j) ≤ b d2 c para todo j ∈ J .
Dem.:
(i) Se existissem i, k diferentes, digamos i < k , tais que 0 ≤ i, k ≤ l e xi = xk ,
jk−1
jk+1
ji+1
j1−1
j
j
j
j
então Px seria dado por: x0 →1 x1 →2 x2 →3 · · · xi →
· · · → xk → · · · → xl−1 →l
4.1
O problema das árvores geradoras independentes
53
xl . Entretanto, o caminho seguinte também liga x0 a xl , mas possui menos saltos:
jk+1
j1−1
j
j1
j2
j3
x0 → x1 → x2 → · · · xi → · · · → xl−1 →l xl . Portanto, o primeiro caminho não é
o mais curto.
(ii) Suponha que existam i, k diferentes, digamos i < k , tais que 0 ≤ i, k ≤ l e
ji = −jk , então o caminho Px possuiria um
Removendo ji e
Pl número s de
Psaltos.
l
−jk , obteríamos o mesmo caminho já que n=1 (−jn ) =
n=1, (−jn ), mas esse
n6=i,n6=−j
último possui dois saltos a menos e, portanto, é mais curto que Px , o que gera uma
contradição com a hipótese.
(iii) Suponha que exista j = dk em J tal que n(Pk , j) > b d2 c. Então temos em
Px o termo dk (b d2 c + p), com p > 0. Vejamos os dois casos:
d par: Neste caso, o termo que aparece é dk (b d2 c+p), com 0 < p < b d2 c. Se p ≥ d2 ,
então b d2 c+p = d+p0 , sendo d0 < d2 . Se d0 ≥ d2 , repita o raciocínio. Agora observe que
k+1
k+1
k+1
k
dk (b d2 c+p) = dk ( d2 +p) = d 2 +pdk + d 2 − d 2 = dk+1 +pdk − dd2 = dk+1 +(p− d2 )dk .
Resta mostrarmos que |p − d2 | < d2 ,ou seja, que − d2 < p − d2 < d2 . Mas isso é válido,
pois, como p > 0, temos − d2 < p − d2 e, além disso, temos p − d2 < 0 < d2 .
d ímpar: Neste caso, o termo que aparece também é dk (b d2 c+p), mas com 0 < p <
d
b 2 c = d−1
. Se p ≥ d+1
, então b d2 c + p = d + p0 , com p0 < d2 . Se p0 ≥ d+1
, repita o ra2
2
2
k−1
k
k+1
k+1
d
d−1
d
d
ciocínio. Agora observe que dk (b 2 c+p) = dk ( 2 +p) = 2 − 2 +pdk + d 2 − d 2 =
)dk . Resta mostrarmos que |p − d+1
| ≤ d−1
,ou
dk+1 + (p − 12 − d2 )dk = dk+1 + (p − d+1
2
2
2
d+1
d−1
d+1
d−1
d−1
seja, que − 2 ≤ p − 2 < 2 . Mas isso é válido, pois p − 2 < 0 < 2 e, como
p ≥ 1, temos − d2 ≤ d2 + p − 1. Logo, − d2 + 21 ≤ d2 − 12 + p.
Um
quadrado latino
de um conjunto
H
de
é uma matriz quadrada com
n
n2
entradas escolhidas a partir
elementos distintos de tal forma que nenhum dos elemen-
tos ocorre duas vezes em qualquer linha ou coluna da matriz. Um
para um caminho de decomposição
Px é um quadrado latino
HPx = {j ∈ J : n(Px , j) 6= 0}.
to
quadrado latino
(PDLS) com relação a um caminho mais cur-
cujas entradas são escolhidas a partir do conjunto
Em particular, denimos a seguinte matriz.
Denição 4.2 Seja HPx = {j0 , j1 , . . . , jt−1 } com |j0 | < |j1 | < · · ·|jt−1 |. Então a
matriz denida
 abaixo é chamada
j0
j1
 j1
j2

 ..
I(Px ) =  .

 jt−2 jt−1
jt−1 j0
···
···
···
···
···
PDLS rotacional

jt−2 jt−1
jt−1 j0 




jt−4 jt−3 
jt−3 jt−2
crescente
de Px :
A entrada ji+1 é chamada a sucessora de ji e é denotada por succ(I(Px ), ji ),
onde os índices i e i + 1 são tomados módulo t. (Daqui por diante, todas as contas
aplicadas aos índices das entradas em PDLS são tomadas módulo |HPx |.)
4.1
O problema das árvores geradoras independentes
Denição 4.3 Para um caminho mais curto Px , seja r =
54
n(Px , j). Um
PDLS de Px com repetições, denotado por I (Px ), é uma matriz de tamanho t × r
obtida a partir de I(Px ) tal que cada entrada j em uma linha de I(Px ) é substituída
por n(Px , j) repetições de j na mesma linha de I ∗ (Px ).
∗
Como cada linha de
I(Px )
P
j∈HPx
pode ser vista como uma sequência de inteiros, tam-
bém denimos as seguintes sequências.
Denição 4.4 Para um caminho mais curto Px , uma sequência regular R de Px ,
denotada por R = [Px ], é uma sequência de inteiros escolhidos a partir de um linha
de I ∗ (Px ). Em particular, denotamos por R = [Px ]j uma sequência regular R que
contém um salto especíco j ∈ HPx como seu último elemento. Além disso, uma
sequência de inteiros S é chamada uma sequência estendida de Px , denotada por
S = (α · j 0 )|[Px ], se S é obtida a partir de R = [Px ] adicionando α repetições de um
salto j 0 ∈ J antes dos termos da sequência R.
Denição 4.5 Seja A = a1 , a2 , . . . , at uma sequência
de números inteiros. Uma
P
de A é denida como uma soma ki=1 ai para algum k = 1, 2, . . . , t.
Em particular, uma soma-prexo
P restrita é uma soma-prexo que satisfaz k 6= t.
Além disso, denimos FA = { ki=1 ai : k = 1, 2, . . . , t − 1}, como o conjunto que
contém todas as somas-prexo estritas de A.
soma-prexo
Proposição 4.4 Para um caminho mais curto Px , se R e R0 são duas sequências
regulares distintas de Px , então FR ∩ FR0 = ∅.
Dem.: Considere o conjunto HPx = {j0 , j1 , . . . , jt−1 } com |j0 | < |j1 | < · · · <
|jt−1 |. Tome s1 ∈ FR e s2 ∈ FR0 duas somas-prexo estritas quaisquer das sequências
R e R0 , respectivamente. Então, conforme a denição de soma prexo estrita, pelo
menos um salto jk ∈ HPx aparece na decomposição de s1 − s2 ou
de s2 − s1 . Como
Pk−1
d
n(Px , jk−1 ) · |jk−1 | ≤ b 2 c · |jk−1 | < |jk | para todo 1 ≤ k < t − 1 e i=0 n(Px , ji ) · |ji | <
|jk |, o salto jk não pode ser soma de outros saltos em qualquer sequência regular
de Px , exceto ele mesmo. Dessa forma, ocorre ±(s1 − s2 ) 6= 0, ou seja, temos a
desigualdade s1 6= s2 .
Para demonstrar mais propriedades relacionadas com PDLS com relação a um
caminho mais curto a
Px ,
também denimos
HPx = {j ∈ J : −j ∈ HPx }.
Proposição 4.5 Sejam x, y(6= 0) ∈ C(cdm , d) dois vértices tais que y = x + α · j
para algum salto j ∈ HPx ∩ HPy , onde 1 ≤ α ≤ d − n(Px , −j) − n(Py , j). Se R = [Px ]
e R0 = (α · j)|[Py ]j , então FR ∩ FR0 = ∅.
4.1
O problema das árvores geradoras independentes
Dem.:
55
j
x ⇒α y juntamente com Py e Px , são dois caminhos que ligam x e
m
0 em C(cd , d). Sejam s1 ∈ FR e s2 ∈ FR0 duas somas-prexo estritas quais/ HPx e
quer de R e R0 , respectivamente. Como j ∈ HPx , isto implica que j ∈
n(Px , −j) > 0. Assim, a decomposição de s1 não inclui o termo j . Por outro lado,
uma vez que j ∈ HPy , isso implica que −j ∈
/ HPy e n(Py , j) > 0. Assim, a decomposição de s2 não inclui o termo −j . Como j é o primeiro elemento em R0 e
α + n(Py , j) ≤ d − n(Px , −j) < d, a decomposição de s2 sempre contém o termo j .
Além disso, como α + n(Px , −j) ≤ d − n(Py , j) < d, o termo n(Px , −j) não pode ser
o complemento de α sob a base de d. Assim, s1 6= s2 .
Proposição 4.6 Sejam x, y(6= 0) ∈ C(cdm , d) dois vértices tais que y = x − j pa-
ra algum salto j ∈ HPy − (HPx ∪ HPx ). Se R = [Px ] e R0 = (−j)|[Py ]j , então
FR ∩ FR0 = ∅.
−j
Dem.: x →
y juntamente com Py e Px são dois caminhos que ligam os vértices
x e 0 em C(cdm , d). Tome s1 ∈ FR e s2 ∈ FR0 duas somas-prexo estritas quaisquer
/ HPx e
de R e R0 , respectivamente. Como j ∈
/ HPx ∪ HPx , isto implica que j ∈
−j ∈
/ HPx . Assim, a decomposição de −(x + s1 ) não inclui os termos j e −j . Por
outro lado, uma vez que Py contém j como um salto, isto implica que −j ∈
/ HPy .
0
Além disso, como j é o último elemento em R , a decomposição de −(x + s2 ) sempre
contém o termo j . Portanto, −(x+s1 ) 6= −(x+s2 ), e isto implica ainda que s1 6= s2 .
Proposição 4.7 Sejam x, y, z(6= 0) ∈ C(cdm , d) tais que y = x + α · j e z =
x + β · j 0 são dois vértices distintos para saltos j ∈ HPy ∩ HPz e j 0 ∈ HPz , onde
1 ≤ α ≤ d − n(Pz , −j) − n(Py , j) e β ≥ 1. Se R = (α · j)|[Py ]j e R0 = (β · j 0 )|[Pz ]j 0 ,
então FR ∩ FR0 = ∅.
j
j0
Dem.: x ⇒
α y junto com Py e x ⇒β z junto com Pz são dois caminhos que
conectam x e 0 em C(cdm , d). Sejam s1 ∈ FR e s2 ∈ FR0 somas-prexo estritas
quaisquer de R e R0 , respectivamente. Como j ∈ HPz , isto implica que j ∈
/ HPz
e n(Pz , −j) > 0. Portanto, a decomposição de s2 não inclui o termo j . Como
j 0 ∈ HPz , temos j 6= j 0 . Por outro lado, como j ∈ HPy , isto implica que n(Py , j) > 0
e a decomposição de s1 não inclui o termo −j . Como j é o primeiro elemento em
R e α + n(Py , j) ≤ d − n(Pz , −j) < d, a decomposição de s1 sempre contém o termo
j . Mais ainda, como α + n(Pz , −j) ≤ d − n(Py , j) < d, o termo n(Pz , −j) não pode
ser o complemento de α sob a base d. Portanto, s1 6= s2 .
4.2
O problema das árvores geradoras independentes
56
Proposição 4.8 Sejam x, y, z(6= 0) ∈ C(cdm , d) tais que y = x − j e z = x − j 0 são
dois vértices distintos para saltos j ∈ HPy − (HPz ∪ HPz ) e j 0 ∈ HPz − (HPy ∪ HPy ).
Se R = (−j)|[Py ]j e R0 = (−j 0 )|[Pz ]j 0 , então FR ∩ FR0 = ∅.
−j
j0
Dem.: x →
y junto com Py e x → z junto com Pz são dois caminhos que conectam x e 0 em C(cdm , d) e j 6= j 0 . Sejam s1 ∈ =R e s2 ∈ =R0 duas somas-prexo
/ HPy ∪ HPy , a decomposição
de R e R0 , respectivamente. Como j ∈
/ HPz ∪ HPz e j ∈
de −(x + s2 ) (respectivamente, −(x + s1 )) não inclui os termos j e −j (respectivamente, j 0 e −j 0 ). Por outro lado, como R contém j como seu último elemento, a
decomposição de −(x + s1 ) sempre contém o termo j . De forma análoga, como R0
contém j 0 como seu último elemento, a decomposição de −(x + s2 ) sempre contém
o termo j 0 . Portanto, −(x + s1 ) 6= −(x + s2 ) e, consequentemente, s1 6= s2 .
Proposição 4.9 Sejam x, y, z(6= 0) ∈ C(cdm , d) tais que y = x + α · j e z = x − j 0
são dois vértices distintos para saltos j ∈ HPy ∩ HPz e j 0 ∈ HPz , onde 1 ≤ α ≤
d − n(Pz , −j) − n(Py , j). Se R = (α · j)|[Py ]j e R = (−j 0 )|[Pz ]j 0 , então FR ∩ FR0 = ∅
−j 0
a
Dem.: x ⇒
b y junto com Py e x → z junto com Pz são dois caminhos que ligam
x e 0 em C(cdm , d) e j 6= j 0 . Sejam s1 ∈ FR e s2 ∈ FR0 duas somas-prexo estritas
quaisquer de R e R0 , respectivamente. De um argumento similar ao da Proposição
4.5, mudando Px por Pz , podemos mostrar que s1 6= s2 .
4.2
Construindo IST's em
C(cdm, d)
com
d>2
Nesta seção, apresentamos um algoritmo de Yanga (2009) para resolver o problema de encontrar árvores geradoras independentes (IST's) em RC-grafos com d > 2.
m
Seja x um vértice qualquer em C(cd , d) e suponha que x = (xm xm−1 · · · x1 x0 )d é rem
m−1
presentado como um inteiro com base d. Então x = xm d +xm−1 d
+· · ·+x1 d+x0 :
Note que
0 ≤ xi < d
para
i = 0, 1, . . . , m − 1
Shortest-Path
e
0 ≤ xm < c .
O seguinte procedi-
Px
x e 0). Como uma substituição para
listar os vértices de Px , estabelecemos o conjunto HPx . Para simplicar as notações
no algoritmo, escrevemos H no lugar de HPx , e n(j) no lugar de n(Px , j) para cada
salto j ∈ J .
mento chamado
será usado para encontrar o caminho mais curto
(isto é, um caminho mais curto entre os vértices
Procedimento Shortest-Path(x)
begin
1.
2.
3.
H = ∅; Carry = 0;
For i = 0 to m − 1 do
if 0 < xi ≤ bd/2c
4.2
O problema das árvores geradoras independentes
4.
5.
else
6.
7.
8.
else
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
57
H = H ∪ {−di }; n(−di ) = xi ; n(+di ) = 0;
Carry = 0;
if bd/2c < xi ≤ d − 1
H = H ∪ {+di }; n(+di ) = d − xi ; n(−di ) = 0;
xi+1 = xi+1 + 1; Carry = 1;
n(−di ) = n(+di ) = 0;
if Carry = 1
xi+1 = xi+1 + 1;
endif
enddo
if c ≥ 2 and 0 < xm ≤ bc/2c
else
else
H = H ∪ {−dm }; n(−dm ) = xm ; n(+dm ) = 0;
if c > 2 and bc/2c < xm ≤ c − 1
H = H ∪ {+dm }; n(+dm ) = c − xm ; n(−dm ) = 0;
20.
n(−dm ) = n(+dm ) = 0;
endif
end Shortest-Path
21.
Como resultado, um caminho mais curto
em cada linha na matriz
∗
I (Px ).
Px
Por exemplo,
pode ser descrito usando os saltos
−50
−50
+52
+52
P = (327 → 326 → 325 → 350 →
+53
3
é um caminho mais curto de 327 = (2302)5 em C(4 × 5 , 5).
m
Para cada vértice x(6= 0) ∈ C(cd , d), de acordo com o caminho mais curto
375 → 0)
denimos
Px ,
{j ∈ J − {±dm } : −j ∈ HPx } se c = 2
(1)
se c 6= 2
{j ∈ J : −j ∈ HPx }
Para cada i ∈ {0, 1, . . . , δ − 1}, denimos λ(i) = min{i, δm − 1 − i} e seja
− se i ≤ λ(i)
sign(i) =
+ se i > λ(i)
Usando um conjunto de regras referentes a HPx e HP , podemos determinar o
x
pai de x em cada árvore geradora T ∈ =, onde = é o conjunto de todas as IST's
m
construídas pelo algoritmo. Para cada vértice x(6= 0) ∈ C(cd , d), realizamos o
HPx =
seguinte procedimento:
Procedimento:
begin
Gen-Parents(x)
HPx , HPx e J − (HPx ∪ HPx ) para x;
for i = 0 to δm − 1 do
j = sign(i) × dλ(i) ; 
 x + succ(I(Px ), j) se j ∈ HPx ;
sign(i)
x+j
se j ∈ HP ;
parent(Tλ(i) , x) =
x

x−j
caso contrário
1. Determine
2.
3.
4.
5.
enddo
end Gen-Parents
(2)
4.2
O problema das árvores geradoras independentes
58
Através do Algoritmo Gen-Parents, podemos determinar os pais de cada vértice,
em todas as árvore geradoras independentes. A partir dessas informações, é possível
desenhar todas as
δm
árvores do conjunto
=.
Exemplo 4.4 Retornando ao grafo do Exemplo 4.3 e utilizando o Algoritmo GenParentes, que apresentamos nessa seção, podemos obter todas as árvores geradoras
independentes de C(2 × 32 , 3).
Figura 4.7: Árvore
T0−
do grafo
C(18, 3)
Figura 4.8: Árvore
T0+
do grafo
C(18, 3)
4.3
O problema das árvores geradoras independentes
Figura 4.9: Árvore
T1−
do grafo
C(18, 3)
Figura 4.10: Árvore
T1+
do grafo
C(18, 3)
Figura 4.11: Árvore
T2−
do grafo
C(18, 3)
59
4.3
O problema das árvores geradoras independentes
4.3
60
Prova da vericidade do algoritmo
Nesta seção, provamos resultados que demonstram a veracidade do Algoritmo
sign(i)
. Por conveniência, denotamos por Ti o grafo Tλ(i)
e vamos considerar
λ(i)
= sign(i) × d . Os Lemas 4.1 e 4.2 mostram que se j ∈
/ HPx , então existe um
Gen Parents
j
vértice
y
no caminho
Ti [x, 0]
de forma que temos
j ∈ HPy .
Lema 4.1 Seja x(6= 0) um vértice qualquer em C(cdm , d) e j = sign(i)×dλ(i) ∈ HPx
para algum 0 ≤ i ≤ δm −1. Se λ(i) 6= m ou c > 2 , então existe um vértice y = x+α·j
tal que j∈ HPy onde
d − n(Px , −j) − n(Py , j) se λ(i) 6= m
α=
c − n(Px , −j) − n(Py , j) caso contrário
Dem.: Suponha x = (xm xm−1 · · · x1 x0 )d e seja HPx = {j0 , j1 , · · · , jt−1 } com
|j0 | < |j1 | < · · · < |jt−1 | . Se c = 1, ±dm ∈
/ J , pois J = {±dk , 0 ≤ k ≤ dlogd 1 ×
dm e − 1} e, por (1), dm ∈
/ HPx se c = 2. Em particular, se dm ∈ HPx , então c > 2.
Como j ∈ HPx , assumimos que j = −jp para algum p com 0 ≤ p ≤ t − 1 . Vamos
agora considerar os dois casos seguintes (para λ(i) = m, consideramos d como c na
prova):
Caso 1: i ≤ λ(i). Neste caso, j < 0 e −j = jp = di ∈ Px . De fato, n(Px , −j) =
n(Px , di ) = d − xi onde b d2 c < xi ≤ d − 1. Sejam α = xi − b d2 c e y = x +
α · j , que é representado por (ym ym−1 · · · y1 y0 )d . Então yk = xk para cada k ∈
{0, 1, . . . , i − 1, i + 1, i + 2, . . . , m} e yi = b d2 c. Aplicando o Procedimento ShortestPath a y , obtemos n(Py , j) = n(Py , −di ) = b d2 c > 0, e então j ∈ HPy . Portanto,
α + n(Px , −j) + n(Py , j) = (xi − b d2 c) + (d − xi ) + b d2 c = d.
0
Caso 2: i > λ(i). Neste caso, j > 0 e −j = jp = −di ∈ Px onde i0 = δm − 1 − i.
0
De fato, n(Px , −j) = n(Px , −di ) = xi0 onde 0 < xi0 ≤ b d2 c. Sejam α = b d2 c + 1 − xi0
e y = x + α · j que é representada por (ym ym−1 · · · y1 y0 )d . Então yk = xk para cada
k ∈ {0, 1, . . . , i0 +1, i0 +2, . . . , m} e yi0 = b d2 c+1. Aplicando o Procedimento Shortest0
Path para y , obtemos n(Py , j) = n(Py , di ) = d − (b d2 c + 1) > 0 e então j ∈ HPy .
Dessa forma, α + n(Px , −j) + n(Py , j) = (b d2 c + 1 − xi0 ) + xi0 + (d − b d2 c − 1) = d.
Lema 4.2 Seja x(6= 0) um vértice qualquer em C(cdm , d). Se j = sign(i) × dλ(i) ∈/
(HPx ∪ HPx ) para algum 0 ≤ i ≤ δ − 1, então existe um vértice y = x − j (isto é,
y = pai(Ti , x)) tal que j ∈ HPy . Em particular, HPy = HPx ∪ {j}.
Dem.: Por (2), se j ∈ J − (HPx ∪ HPx ), então y = x − j . Como j ∈/ HPx e
j∈
/ HPx , o conjunto HPx não contém os saltos j e −j . Obviamente, HPy = HPx ∪{j}
e, portanto, j ∈ HPy .
4.3
O problema das árvores geradoras independentes
Por questão de conveniência, usaremos
quando
λ(i) = m
e
c > 2.
d
no lugar de
61
c
deste ponto em diante
Os lemas 4.3 e 4.4 nos auxiliarão para mostrar a inde-
pendência de dois caminhos.
Lema 4.3 Seja x(6= 0) um vértice qualquer em C(cdm , d) e suponha que j, j 0 ∈ HPx ,
onde j = sign(i) × dλ(i) e j 0 = sign(i0 ) × dλ(i ) , com 0 ≤ i, i0 ≤ δm − 1 e i 6= i0 . Se
y = x + α · j e z = x + β · j 0 são dois vértices em C(cdm , d) e |j| < |j 0 |, então j ∈ HPz
e α + n(Pz , −j) + n(Py , j) = d.
Dem.: Seja HPx = {j0 , j1 , . . . , jt−1 } com |j0 | < |j1 | < · · · < |jt−1 |. Como
j, j 0 ∈ HPx e |j| < |j 0 |, assumimos que j = −jp e j 0 = −jq sendo 0 ≤ p < q ≤ t − 1.
Pelo Lema 4.1, precisamos apenas considerar λ(i0 ) 6= m ou c > 2. Além disso, j ∈ HPy e α = d − n(Px , −j) − n(Py , j). Também temos j 0 ∈ HPz e β =
d − n(Px , −j 0 ) − n(Pz , j 0 ). Como y = x + (d − n(Px , −j) − n(Py , j)) · j , temos HPy =
{j0 , j1 , . . . , jp−1 , j, . . . , j|HPy |−1 }, onde n(Py , jk ) = n(Px , jk ) para todo 0 ≤ k ≤ p − 1,
e o número de repetições de j em Py é ou b d2 c ou d − b d2 c − 1 que é determinado por
i ≤ λ(i) ou i > λ(i). De forma análoga, como z = x + (d − n(Px , −j 0 ) − n(Pz , j 0 )) · j 0 ,
temos HPz = {j0 , j1 , . . . , jq−1 , j 0 , . . . , j|HPz |−1 }, onde n(Pz , jk ) = n(Px , jk ) para todo
0 ≤ k ≤ q−1 e o número de repetições de j 0 em Pz é ou b d2 c ou d−b d2 c−1 que é determinado por i0 ≤ λ(i0 ) ou i0 > λ(i0 ). De HPy e HPz bem como p < q , podemos ver que
existe um salto jr ∈ HPz tal que jr = jp = −j , onde 0 ≤ r ≤ q − 1. Como um resultado, −j ∈ HPz se, e somente se, j ∈ HPz , Além disso, α + n(Pz , −j) + n(Py , j) = d
segue do fato que n(Pz , −j) = n(Px , −j).
0
Lema 4.4 Seja x(6= 0) um vértice qualquer
em C(cdm , d) e suponha que j = sign(i)×
0
dλ(i) ∈ HPx e j 0 = sign(i0 ) × dλ(i ) ∈
/ (HPx ∪ HPx ) onde 0 ≤ i, i0 ≤ δm − 1.
Se y = x + α · j e z = x − j 0 são dois vértices em C(cdm , d), então j ∈ HPz e
α + n(Pz , −j) + n(Py , j) = d.
Dem.: Como j ∈ HPx e j 0 ∈/ HPx , j 6= j 0 . Seja HPx = {j0 , j1 , . . . , jt−1 } com
|j0 | < |j1 | < · · · < |jt−1 |. Como j ∈ HPx , assumimos que j = −jp para algum
0 ≤ p ≤ t−1. Pelo Lema 4.1, j ∈ HPy e α = d−n(Px , −j)−n(Py , j). Por outro lado,
como j 0 ∈
/ HPx ∪ HPx , o Lema 4.2 mostra que HPz = HPx ∪ {j 0 }, e isto implica ainda
que n(Pz , jk ) = n(Px , jk ) para todo salto jk ∈ HPz − {j 0 }. Portanto, −j = jp ∈ HPx
implica que −j ∈ HPz e j ∈ HPz . Além disso, α + n(Pz , −j) + n(Py , j) = d segue
do fato que n(Pz , −j) = n(Px , −j).
O lema seguinte mostra que todo subgrafo construído em
árvore geradora.
=
é, de fato, uma
4.3
O problema das árvores geradoras independentes
62
Lema 4.5 Para todo inteiro i com 0 ≤ i ≤ δm − 1, Ti é uma árvore geradora
enraizada em 0 no grafo C(cdm , d).
Dem.: Seja j = sign(i) × dλ(i) . É direto do Procedimento Gen-Parents que
para todo vértice x(6= 0) ∈ C(cdm , d) tem-se x ∈ Ti . Portanto, o grafo resultante
é um subgrafo gerador de C(cdm , d). Para completar a prova, precisamos mostrar
que existe um único caminho de todo vértice x(6= 0) a 0 em Ti , pois isso garante
que a árvore não possui ciclo. Em particular, o vértice −j é adjacente a 0 em Ti .
Suponha que HPx = {j0 , j1 , . . . , js−1 } com |j0 | < |j1 | < · · · < |js−1 |. Então cada
n(Px , jk ), k = 0, 1, . . . , s − 1, no caminho mais curto Px , pode ser calculado pelo
Procedimento Shortest-Path. De acordo com j , podemos considerar os seguintes
casos:
Caso 1: j ∈ HPx . Suponha que j = jp para algum p = 0, 1, . . . , s − 1. Como
jp+1 = succ(I(Px ), jp ), x é adjacente a x + jp+1 em Ti pelo passo 4 do procedimento
Gen-Parents(x). Seja y = x + n(Px , jp+1 ) · jp+1 . Então Py é um subcaminho de
Px e HPy = {j0 , j1 , . . . , jp , jp+2 , . . . , js−1 }. Portanto, n(Py , jk ) = n(Px , jk ) para todo
jk ∈ HPy . Como jp ∈ HPy e jp+2 = succ(I(Py ), jp ), y é adjacente a y + jp+2 em
Ti pelo passo 4 do procedimento Gen-Parents(x). Seja z = y + n(Py , jp+2 ) · jp+2 .
Então Pz é um subcaminho de Py e HPz = {j0 , j1 , . . . , jp , jp+3 , . . . , js−1 }. Portanto, n(Pz , jk ) = n(Py , jk ) para todo jk ∈ HPz . Novamente, pelo passo 4 de GenParents(x), z é adjacente a z + jp+3 em Ti . Desta forma, podemos encontrar o
seguinte caminho único que liga x a 0 em Ti :
jp+1
jp+2
Ti [x, 0] : x ⇒ n(Px ,jp+1 ) (x + n(Px , jp+1 ) · jp+1 ) ⇒ n(Px ,jp+2 ) (x + n(Px , jp+1 ) · jp+1 +
jp+3
jp−1
jp
n(Px , jp+2 ) · jp+2 ) ⇒ n(Px ,jp+3 ) · · · ⇒ n(Px ,jp−1 ) (−n(Px , jp ) · jp ) ⇒n(Px ,jp ) 0.
Caso 2: j ∈ HPx . Pelo passo 4 de Gen-Parents(x) , x é adjacente a x + j em
Ti . Por (1), se c = 2, então j 6= ±dm e isso implica ainda que λ(i) 6= m. Caso
contrário, decorre de Shortest=Path que ou c > 2 ou c = 1 e λ(i) 6= m. Assim, pelo
Lema 4.1, existe um vértice y = x + α · j , onde α = d − n(Px , −j) − n(Py , j) tal que
j ∈ HPy . Além disso, demonstramos no caso 1 que existe um único caminho Ti [y, 0]
j
que liga y e 0 em Ti . Portanto, x ⇒α y junto com o caminho Ti [y, 0] forma o único
caminho de ligação entre x e 0 em Ti .
Caso 3:. j ∈ J − (HPx ∪ HPx ). Pelo passo 4 de Gen-Parents(x), x é adjacente a
x − j em Ti . Seja y − j . Pelo Lema 4.2, j ∈ HPy . Além disso, mostramos no caso
−j
1 que existe um caminho único Ti [y, 0] que liga y e 0 em Ti . Portanto, x → y junto
com o caminho Ti [y, 0] forma o único caminho de ligação entre x e 0 em Ti .
Vamos agora mostrar a independência das IST's no conjunto de árvores
=
que
construímos no algoritmo.
Lema 4.6 Para 0 ≤ i, i0 ≤ δm − 1 e i 6= i0 , Ti e Ti0 são IST enraizadas em 0 no
grafo C(cdm , d).
Dem.: Sejam 0x(6= 0) um vértice qualquer de C(cdm , d), j = sign(i) × dλ(i) e
0
j = sign(i0 ) × dλ(i ) . Consideremos os seguintes casos:
4.3
O problema das árvores geradoras independentes
63
Caso 1: j, j 0 ∈ HPx . Segue da Proposição 4.4 que Ti [x, 0]||Ti0 [x, 0].
Caso 2: j ∈ HPx e j 0 ∈ HPx . Pelo Lema 4.5, Ti [x, 0] tem j como seu último salto
j0
e existe um vértice y = x + α · j 0 tal que x ⇒α y junto com o caminho Ti0 [y, 0] forma
o único caminho de ligação entre x e 0 em Ti0 . Em particular, Ti [y, 0] possui j 0 como
seu último salto. Pelo Lema 4.1, temos j 0 ∈ HPy e α = d − n(Px , −j 0 ) − n(Py , j 0 ).
Sejam R = [Px ]j e R0 = (α · j 0 )|[Py ]j 0 . Como j 0 ∈ HPx ∩ HPy , pela Proposição 4.5,
se s1 ∈ =R e s2 ∈ =R0 , então s1 6= s2 . Assim, Ti [x, 0]||Ti0 [x, 0].
Caso 3: j ∈ HPx e j 0 ∈ J − (HPx ∪ HPx ). De acordo com o Lema 4.5, Ti [x, 0]
−j 0
possui j como seu último salto e existe um vértice y = x − j 0 tal que x → y juntamente com o caminho Ti0 [y, 0] forma o único caminho de ligação entre os vértices x
e 0 em Ti0 . A árvore Ti0 [y, 0] possui j 0 como seu último salto. Assim, j 0 ∈ HPy . Seja
R = [Px ]j e R0 = (−j 0 )|[Py ]j 0 . Como j 0 ∈
/ HPx ∪ HPx e j 0 ∈ HPy , pela Proposição
4.6, se s1 ∈ =R e s2 ∈ =R0 , então s1 6= s2 . Portanto, Ti [x, 0]||Ti0 [x, 0].
Caso 4: j, j 0 ∈ HPx . Pelo Lema 4.5, existe um vértice y = x + α · j tal que
j
x ⇒α y junto com o caminho Ti [y, 0] forma o único caminho de ligação entre x
j0
e 0 em Ti . Da mesma forma, existe um vértice z = x + β · j 0 tal que x ⇒β z ,
juntamente com o caminho Ti0 [z, 0] forma o único caminho de ligação entre x e 0
em Ti0 . Em particular, Ti [y, 0] possui j como seu último salto e Ti0 [z, 0] tem j 0 como
seu último salto. Assim, j ∈ HPy ej 0 ∈ HPz . Podemos assumir que |j| < |j 0 |, sem
perda de generalidade. Pelo Lema 4.3, j ∈ HPz e α + n(Pz , −j) + n(Py , j) = d.
Sejam R = (α · j)|[Py ]j e R0 = (β · j 0 )|[Pz ]j 0 . Como j ∈ HPy ∩ HPz e j 0 ∈ HPz , pela
Proposição 4.7, se s1 ∈ =R e s2 ∈ =R0 , então s1 6= s2 . Assim, Ti [x, 0]||Ti0 [x, 0].
Caso 5: j, j 0 ∈ J −(HPx ∪HPx ). Pelo Lema 4.5, existe um vértice y = x−j tal que
−j
x → y junto com o caminho Ti [y, 0] forma o único caminho que liga x e 0 na árvore
−j 0
Ti . Da mesma forma, existe um vértice z = x − j 0 tal que x → z juntamente com o
caminho Ti0 [z, 0] forma o único caminho de ligação entre x e 0 em Ti0 . Ti [y, 0] possui
j como seu último salto e Ti0 [z, 0] tem j 0 como seu último salto. Assim, j ∈ HPy e
/ HPx ∪ HPx , nenhum dos termos j, −j, j 0 e −j 0 estão contidos
j 0 ∈ HPz . Como j, j 0 ∈
em HPx ou HPx . Pelo Lema 4.2, HPy = HPx ∪ {j} e HPz = HPx ∪ {j 0 }. Isso mostra
/ HPy ∪ HPy . Sejam R = (−j)|[Py ]j e R0 = (−j 0 )|[Pz ]. Como
que j ∈
/ HPz ∪ HPz e j 0 ∈
j ∈ HPy − (HPz ∪ HPz ) e j 0 ∈ HPz − (HPy ∪ HPy ), pela Proposição 4.8, se s1 ∈ =R e
s2 ∈ =R0 , então s1 6= s2 . Assim, Ti [x, 0]||Ti0 [x, 0].
Caso 6: j ∈ HPx e j 0 ∈ J − (HPx ∪ HPx ). Conforme o Lema 4.5, temos um
j
vértice y = x + α · j tal que x ⇒α y juntamente com o caminho Ti [y, 0] forma o
único caminho de ligação entre os vértices x e 0 na árvore Ti . Além disso, existe
−j 0
um vértice z = x − j 0 tal que x → z , juntamente com o caminho Ti [z, 0] forma
o único caminho de ligação entre os vértices x e 0 na árvore Ti0 . Ti [y, 0] possui j
como seu último salto e Ti0 [z, 0] tem j 0 como seu último salto. Assim, j ∈ HPy e
j 0 ∈ HPz . Pelo Lema 4.4, j ∈ HPz e α + n(Pz , −j) + n(Py , j) = d. Considere as
sequências R = (α · j)|[Py ]j e R0 = (−j 0 )|[Pz ]j 0 . Como j ∈ HPy ∩ HPz e j 0 ∈ HPz ,
pela Proposição 4.9, se s1 ∈ =R e s2 ∈ =R0 , então s1 6= s2 . Assim, Ti [x, 0]||Ti0 [x, 0].
Como escolhemos x arbitrariamente no grafo C(cdm , d), as árvores Ti e Ti0 são
independentes.
4.4
O problema das árvores geradoras independentes
64
Combinando os lemas 4.5 e 4.6, temos o seguinte teorema:
Teorema 4.1 O algoritmo de construção de δm IST's em C(cdm , d) com d > 2 pode
ser executado na complexidade de tempo O(mN ), onde N = c × dm .
Conforme o Teorema 4.1, o algoritmo pode ser paralelizado em
O(N )
4.4
processadores para rodar em complexidade de tempo
C(cdm , d) usando
O(m).
IST's em grafos gaussianos
Finalizando o trabalho, foi feita uma busca para um algoritmo que determine possíveis árvores geradoras independentes em grafos gaussianos, o que é inédito na
literatura até então.
O mesmo foi implementado e o programa resultante gerou
resultados para alguns grafos gaussianos.
A ideia foi tomar o vértice
0 + 0i
como raiz.
A partir dele, são construídas 4
árvores, sendo que cada uma delas possui como lho um dos 4 vértices adjacentes a
0 + 0i
(Grafos Gaussianos possuem grau 4). Cada lho, é pai dos outros 3 vértices
adjacentes a ele. Desses últimos, são tomados como lhos os adjacentes a eles que
ainda não aparecem na árvore, sendo que a construção é feita seguindo uma ordem
prexada, da direita para esquerda, entre folhas que estão no mesmo nível da árvore.
Esse ordenamento é feito baseado na estrutura do grafo gaussiano, onde cada vértice
possui um adjacente acima, um abaixo, um a direita e outro a esquerda. Seguindo
os passos anteriores e fazendo o mesmo para todos os vértices que surgirem na
construção, obtemos as 4 árvores.
Observe que, usando esse raciocínio, 4 árvores são sempre construídas, mas não
há a garantia de que elas são independentes. Por isso, após a construção, vericamos
quais dessas árvores são independentes entre si, fazendo uma comparação entre todas
as combinações de pares de árvores.
Na implementação do programa, utilizamos a idéia de listas, estruturas de dados
bem conhecidas, e uma série de funções auxiliares para exibir árvores geradoras dessa
classe especíca de grafos, cujo conhecimento teórico foi desenvolvido ao longo da
dissertação. É importante lembrar que, por ter um algoritmo de roteamento mais
simples, e uma rotulação de vértices mais conveniente para se trabalhar em relação
aos grafos circulantes, essas IST's podem ter grande utilidade em problemas reais.
Os códigos-fontes desse último programa também estão presentes no Anexo 1.
Exemplo 4.5 Consideremos o grafo Gaussiano G2+3i . Executando o programa,
obtemos as árvores 2 e 4 são independentes, assim como as árvores 3 e 4 o são.
4.4
O problema das árvores geradoras independentes
Figura 4.12: Árvore 2 gerada pelo programa
Figura 4.13: Árvore 3 gerada pelo programa
Figura 4.14: Árvore 4 gerada pelo programa
As árvores também podem ser vistas da seguinte forma:
65
4.4
O problema das árvores geradoras independentes
Figura 4.15: Árvore Geradora 2
Figura 4.16: Árvore Geradora 3
Figura 4.17: Árvore Geradora 4
66
Capítulo 5
Conclusão e Trabalhos Futuros
5.1
Conclusão
Este trabalho desenvolve algoritmos para o roteamento em diferentes tipos de redes
interligadas modeladas por grafos circulantes e gaussianos, fazendo uso, sobretudo,
de conceitos e resultados de álgebra avançada e de ferramentas de computação paralela.
Em um primeiro momento, o Anel dos Inteiros Gaussianos foi estudado com
mais detalhes.
Também foram estudados alguns resultados sobre os grafos circu-
lantes e grafos gaussianos, objetos matemáticos utilizados nas modelagens das redes
interligadas que consideramos. Todas as demonstrações foram refeitas e provas alternativas foram sugeridas.
c
Foram desenvolvidos, através do software MATLAB , programas que ilustram
os grafos circulantes e gaussianos, considerados no trabalho.
Um programa foi implementado para apresentar uma visualização alternativa
para o grafo Gaussiano, cuja topologia chamaremos losangular. Nela, cada vértice
do mesmo é transformado no elemento que possui a menor norma em sua classe de
equivalências de
Gα
e as adjacências são preservadas. Obviamente, esse novo grafo
gerado é isomorfo ao obtido anteriormente. Os códigos-fontes dos programas estão
presentes no Anexo 1.
Para a solução do problema de roteamento em grafos gaussianos e em grafos
circulantes foram desenvolvidos também programas que ilustram as melhores rotas
nas duas classes de de grafos estudados.
Foram implementados também programas para busca de árvores geradoras independentes (IST's) em RC-Grafos baseados nos resultados teóricos provados no
Capítulo 4. Neles, é possível saber qual o pai de cada vértice em uma determinada
árvore. Cada uma delas é ilustrada separadamente apenas com os parâmetros de
entrada
c, d
e
m,
que caracterizam o Grafo Circulante Recursivo no qual é feita a
pesquisa das IST's.
Além disso, o trabalho propõe uma algoritmo eciente para se encontrar IST's
em grafos gaussianos em geral.
Os resultados obtidos possuem grande relevância pelo fato de atualmente o
número de redes interligadas está cada vez maior, uma vez que sistemas paralelizados
estão mais frequentes, e a comunicação destas redes pede mais eciência na transmissão de um ponto a outro das mesmas. Podemos notar uma interdisciplinaridade
67
5.2
Conclusão e Trabalhos Futuros
68
no estudo da matemática avançada para solucionar problemas práticos no campo
da computação.
5.2
Trabalhos Futuros
A partir do estudo apresentado, podemos sugerir algumas opções para possíveis
trabalhos futuros:
•
Encontrar algoritmos de roteamento e visualização, com funções semelhantes
aos apresentados ao longo do texto, mas sob um paradigma de programação
diferente, o de orientação a objetos, o que permitiria a implementação na
plataforma JAVA, por exemplo.
•
Procurar estruturas algébricas que seja capazes de gerar grafos tridimensionais.
•
Desenvolver novos algoritmos para busca de árvores geradoras independentes
em Grafos Gaussianos, que encontrem tais árvores em um número maior de
grafos.
Referências
BERMOND, J.-C.; COMELLAS, F.; HSU, D.F.,
Distributed loop computer
networks: A survey, Jornal of Parallel and Distributed Computings 24 (1995)
2-10
BEIVIDE, R.; HERRADA, E.; BALCBAZAR, J. L.; ARRUABARRENA, A.
Optimal Distance Networks of Low Degree for Parallel Computers, IEEE
Trans. Computer, vol. 40, no. 10, Octuber 1991.
CAI, J.-Y.; HAVAS, G.; MANS, B.; NERURKAR, A.; SEIFERT, J.-P.;
SHPARLINSKI, I.
On Routing in Circulant Graphs, Proc.
Fifth Ann. Int'l
Computing and Combinatorics Conf., 1999.
A Discrete
Optimization Problem in Local Networks and Data Alignment, IEEE
FIOL, M.A.; YEBRA, J.L.; ALEGRE, I.; VALERO, M.
Trans. Computers, vol. 36, no. 6, pp. 702-713, June 1987.
GILBERT, W. J.
Modern Algebra with applications, second edition, United
States of America, Wiley-Interscience, 2004, 349 p.
Otimização combinatória e programação linear:
modelos e algoritmos, Rio de Janeiro, Editora Campus, 2000, p. 276-279.
GOLDBARG, M. C.
GONÇALVES, A.
Introdução à Álgebra, Rio de Janeiro, IMPA, 1979, 194 p.
HUNGERFORD, T. W.
Abstract Algebra: An Introduction, Second Edition,
Saunders College Publishing, United States of America, 1997.
HUSSAIN, Z. On Shortest Disjoint Paths and Hamiltonian Cycles in
Some Interconnection Networks, 2011, 107 f. Doctor Tesis, Oregon State
University, april 2011.
MARTINEZ, C.
Codes and Graphs over Complex Integer Rings, 2007.
f. Doctoral Thesis, Universidad de Cantabria, Santander, January 2007.
Dense
gaussian networks: Suitable topologies for on-chip multiprocessors,
MARTINEZ, C.; VALLEJO E.; BEIVIDE, R.; IZU, C.; MORETO, M.
International Journal of Parallel Programming, vol. 34, pp.
69
193 − 211,
2006.
107
5.2
Referências
70
MARTINEZ, C.; BEIVIDE, R.; STAFFORD, E.; MORETO, M.; GABIDULIN, E.
Modeling toroidal networks with the gaussian integers, IEEE Transactions
on Computers, vol. 57, no. 8, pp.
NETTO, P. O. B.
1046 − 1056,
2008.
Grafos: teoria, modelos, algoritmos, São Paulo:
Edgard
Blucher, 2006.
Construction Multiple Independent
Spanning trees on Recursive Circulant Graphs G(2m , 2), International
YANG, J. S.; TANG, S. M.. WANG, Y.L
Journal of Foundations of Computer Science Vol.
21,
No. 1 (2010)
YANG, J.-S.; CHANGA, J.-M.; TANGB, S.-M.; WANGC, Y.-L.
73 − 90.
On the
independent spanning trees of recursive circulant graphs G(cdm , d), with
d > 2n ,
Theoretical Computer Science 410, 2009.
Anexo 1
Neste anexo são apresentados os códigos-fontes dos algoritmos desenvolvidos e implementados durante o trabalho.
Algoritmo de Roteamento em Grafos Circulantes
Este algoritmo tem como funcionalidades encontrar um menor caminho entre dois
vértices quaisquer de um grafo circulante e ilustrar o caminho encontrado.
Função Principal:
Menorcaminhocirculante
Funções Auxiliantes:
algoritmo, euclidesest, circulante, Desenhacaminho
Desenhacaminho
function[]=Desenhacaminho(N,z,m,n,A,B)
k=0;
i=m;
%k indica a quantidade de vezes que o salto A é realizado no caminho
%i é variável auxiliar para indicar quais vertices serão ligados
%pela aresta que sera colorida.
arg = (2*pi)/N;
%Ângulo para o grafo circulante (necessario para o
%desenho do caminho)
%Este 'while' faz o caminho com cor azul indicando o número de saltos com A
while (k<abs(z(1)))
k=k+1;
if z(1)>0
%Sentido Anti-Horario (deve-se somar A)
plot([cos((i)*arg) cos((i+A)*arg)],[sin((i)*arg) sin((i+A)*arg)],'y',
[cos((i)*arg) cos((i+A)*arg)], [sin((i)*arg) sin((i+A)*arg)],'oy');
hold on;
i=i+A;
else
%Sentido Horario (deve-se subtrair A)
plot([cos((i)*arg) cos((i-A)*arg)],[sin((i)*arg) sin((i-A)*arg)],'y',
[cos((i)*arg) cos((i-A)*arg)], [sin((i)*arg) sin((i-A)*arg)],'oy');
hold on;
i=i-A;
end
71
5.2
Anexo
72
end
k=0; %A variável k é reutilizada para indicar a quantidade de vezes que o
%salto B é realizado no caminho
%Este 'while' faz o caminho com cor vermelha indicando o número de saltos com B
while (k<abs(z(2)))
k=k+1;
if z(2)>0
%Sentido Anti-Horário (deve-se somar B)
plot([cos((i)*arg) cos((i+B)*arg)],[sin((i)*arg) sin((i+B)*arg)],'r',
[cos((i)*arg) cos((i+B)*arg)], [sin((i)*arg) sin((i+B)*arg)],'or');
hold on;
i=i+B;
else
%Sentido Horário (deve-se subtrair B)
plot([cos((i)*arg) cos((i-B)*arg)],[sin((i)*arg) sin((i-B)*arg)],'r',
[cos((i)*arg) cos((i-B)*arg)], [sin((i)*arg) sin((i-B)*arg)],'or');
hold on;
i=i-B;
end
end
plot(cos((m)*arg),sin((m)*arg),'xk');
plot(cos((m)*arg),sin((m)*arg),'ok');
plot(cos((n)*arg),sin((n)*arg),'xm');
plot(cos((n)*arg),sin((n)*arg),'om');
%Colore
%Colore
%Colore
%Colore
o
o
o
o
end
algoritmo
function[result]=algoritmo(euc,a,b,c)
%Calcula X, Y que satisfaçam aX + bY = c,
%sendo |X| + |Y| mínimo.
%Parâmetros de entrada: a,b,c
%Parâmetros de saída: X,Y
%Restrição que MDC(a,b) seja 1 ou -1
%A(3) = mdc
if euc(3)>0 x0 = euc(1)*c; y0 = euc(2)*c; end
if euc(3)<0 x0 = -euc(1)*c; y0 = -euc(2)*c; end
if a ~= b
t0 = floor((x0+y0)/(a-b));
else
t0=1;
end
vértice
vértice
vertice
vertice
de
de
de
de
origem de preto
origem de preto
destino de amarelo
destino de amarelo
5.2
Anexo
73
t=t0; vant=abs(x0+(t0-1)*b) + abs(y0-(t0-1)*a); m=abs(x0 +(t0)*b) +
abs(y0 - (t0)*a); while(m<=vant)
t=t+1;
vant=m;
m=abs(x0 + b*t) + abs(y0 - a*t);
end z(1)=x0 + b*(t-1); z(2)=y0 - a*(t-1);
t=t0-2; m=abs(x0 + (t0-2)*b) +
(t0-1)*b) + abs(y0- (t0-1)*a);
t=t-1;
vant=m;
m=abs(x0 + b*t) + abs(y0 end w(1)=x0 + b*(t+1); w(2)=y0
abs(y0 - (t0-2)*a); vant=abs(x0 +
while(m<=vant)
a*t);
- a*(t+1);
if abs(z(1))+abs(z(2)) > abs(w(1))+abs(w(2))
result=w;
else
result=z;
end
end
Algoritmo de Roteamento em Grafos Gaussianos
ShortestPath(u, v, w ) busca o menor caminho entre dois vértices de um grafo gaussiano gerado por
w.
O resultado é ilustrado em duas topologias diferentes (em L e
losangular).
Função Principal:
ShortestPah
Funções Auxiliantes:
converter, converterporiginal, gaussiano,
gaussianoconverter
ShortestPath
function[]=ShortestPath(u,v,w)
%u=[x y] : Source
%v=[x' y'] : Destination
%w=[a b] : graph generator
close all; clc a=w(1); b=w(2); N=a^2+b^2;
5.2
Anexo
74
plot(u(1),u(2),'xk'); %Ponto Inicial
plot(v(1),v(2),'xk'); %Ponto Final
hold on; gaussianoconverter(a,b); hold on;
%Faz o desenho do grafo gaussiano com os pontos final e inicial
sem indicar ainda o melhor caminho entre eles
x0 = v(1) - u(1);
y0 = v(2) - u(2);
%x' - x
%y' - y
x(1) = x0 - a; y(1) = y0 - b; s(1) = abs(x(1)) + abs(y(1));
x(2) = x0 + a; y(2) = y0 + b; s(2) = abs(x(2)) + abs(y(2));
x(3) = x0 - b; y(3) = y0 + a; s(3) = abs(x(3)) + abs(y(3));
x(4) = x0 + b; y(4) = y0 - a; s(4) = abs(x(4)) + abs(y(4));
x(5) = x0 + (a-b); y(5) = y0 + (a+b); s(5) = abs(x(5)) + abs(y(5));
x(6) = x0 - (a-b); y(6) = y0 - (a+b); s(6) = abs(x(6)) + abs(y(6));
x(7) = x0 + (a+b); y(7) = y0 + (b-a); s(7) = abs(x(7)) + abs(y(7));
x(8) = x0 - (a+b); y(8) = y0 - (b-a); s(8) = abs(x(8)) + abs(y(8));
x(9) = x0 + 2*a; y(9) = y0 + 2*b; s(9) = abs(x(9)) + abs(y(9));
x(10) = x0 - 2*a; y(10) = y0 - 2*b; s(10) = abs(x(10)) + abs(y(10));
x(11) = x0 - 2*b; y(11) = y0 + 2*a; s(11) = abs(x(11)) + abs(y(11));
x(12) = x0 + 2*b; y(12) = y0 - 2*a; s(12) = abs(x(12)) + abs(y(12));
x(13) = x0; y(13) = y0; s(13) = abs(x(13)) + abs(y(13));
t=converter(v,w);
%Armazena no vetor t qual a posição do vetor de destino (v) no novo
%grafo gaussiano.
menor=s(1); k=1; for i=2:13
if s(i)<=menor
menor=s(i);
k=i;
end
end
%r1 e r2 armazenam o resultado do par encontrado acima
r1 = x(k) r2 = y(k)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Esta parte desenha o caminho entre o vertice de origem e o vertice de
%destino no grafo gaussiano convertido, onde temos:
%Origem: converter([u(1) u(2)],w)
Destino: converter([v(1) v(2)],w)
A=u;
if r1>0
5.2
Anexo
75
for i=1:r1
VA=converter([A(1)
A(2)],w);
VB=converter([A(1)+1 A(2)],w);
A(1)=A(1)+1;
plot([VA(1) VB(1)],[VA(2) VB(2)],'k',[VA(1) VB(1)],[VA(2) VB(2)],'ok');
hold on;
end
end
if r1<0
for i=1:-r1
VA=converter([A(1) A(2)],w);
VB=converter([A(1)-1 A(2)],w);
A(1)=A(1)-1;
plot([VA(1) VB(1)],[VA(2) VB(2)],'k',[VA(1) VB(1)],[VA(2) VB(2)],'ok');
hold on;
end
end
if r2>0
for i=1:r2
VA=converter([A(1) A(2)],w);
VB=converter([A(1) A(2)+1],w);
A(2)=A(2)+1;
plot([VA(1) VB(1)],[VA(2) VB(2)],'k',[VA(1) VB(1)],[VA(2) VB(2)],'ok');
hold on;
end
end
if r2<0
for i=1:-r2
Z=converter([A(1) A(2)],w);
W=converter([A(1) A(2)-1],w);
A(2)=A(2)-1;
plot([Z(1) W(1)],[Z(2) W(2)],'k',[Z(1) W(1)],[Z(2) W(2)],'ok');
hold on;
end
end
%Abaixo faz o desenho dos pontos inicial e final no grafo gaussiano
%convertido.
V=converter([u(1)
u(2)],w);
plot(V(1),V(2),'ok');
V=converter([v(1)
v(2)],w);
plot(V(1),V(2),'ok');
hold on
5.2
Anexo
76
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2) gaussiano(w(1),w(2))
A=u;
if r1>0
for i=1:r1
VA=converterporiginal([A(1)
A(2)],w);
VB=converterporiginal([A(1)+1 A(2)],w);
A(1)=A(1)+1;
plot([VA(1) VB(1)],[VA(2) VB(2)],'k',[VA(1) VB(1)],[VA(2) VB(2)],'ok');
hold on;
end
end
if r1<0
for i=1:-r1
VA=converterporiginal([A(1)
A(2)],w);
VB=converterporiginal([A(1)-1 A(2)],w);
A(1)=A(1)-1;
plot([VA(1) VB(1)],[VA(2) VB(2)],'k',[VA(1) VB(1)],[VA(2) VB(2)],'ok');
hold on;
end
end
if r2>0
for i=1:r2
VA=converterporiginal([A(1) A(2)],w);
VB=converterporiginal([A(1) A(2)+1],w);
A(2)=A(2)+1;
plot([VA(1) VB(1)],[VA(2) VB(2)],'k',[VA(1) VB(1)],[VA(2) VB(2)],'ok');
hold on;
end
end
if r2<0
for i=1:-r2
VA=converterporiginal([A(1) A(2)],w);
VB=converterporiginal([A(1) A(2)-1],w);
A(2)=A(2)-1;
plot([VA(1) VB(1)],[VA(2) VB(2)],'k',[VA(1) VB(1)],[VA(2) VB(2)],'ok');
hold on;
end
end
plot(u(1),u(2),'ok'); plot(v(1),v(2),'ok'); hold on
5.2
Anexo
77
%Este if calcula o diâmetro do grafo
if mod(N,2)==1 %N odd
diametro = b-1
else
%N even
diametro = b end
end
converter
function[D]=converter(alpha,gerador)
%Converte o elemento alpha em G_gerador para o elemento que possui a
%menor norma dentro da sua classe de equivalência.
%gerador = a+bi (gerador do grafo)
%alpha = c+di (elemento a ser convertido)
a=gerador(1); b=gerador(2); c=alpha(1); d=alpha(2); N=a^2+b^2;
D(1)=real(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i));
D(2)=imag(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i)); end
converterporiginal
function[R]=converterporiginal(alpha,gerador)
%Converte o elemento alpha em G_gerador para o elemento que possui a
%menor norma dentro da sua classe de equivalência.
%gerador = a+bi (gerador do grafo)
%alpha = c+di (elemento a ser convertido)
a=gerador(1); b=gerador(2); c=alpha(1); d=alpha(2); N=a^2+b^2;
D(1)=real(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i));
D(2)=imag(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i));
R=D;
if (D(2)>=a)
R(2)=D(2)-a;
R(1)=D(1)+b;
%'cond 1';
end
if ((D(1)<0) && (D(2)<a))
if D(2)>-(b-a+1)
5.2
Anexo
78
R(1)=D(1)+a+b;
R(2)=D(2)+b-a;
%'cond 2';
end
end
if D(2)<-(b-a)
R(1)=D(1)+a;
R(2)=D(2)+b;
%'cond 3 part1';
end
if ((D(1)>=0) && (D(2)<0))
R(1)=D(1)+a;
R(2)=D(2)+b;
%'cond 3 part2'
end
end
gaussiano
function[ ]=gaussiano(a,b)
%Plota num plano bidimensional o grafo gaussiano com parâmetros a e b
%Restrição: 0<= a <=b
%linhas horizontais inferiores
for k=0:a-1
for m=0:a+b-2
plot([m m+1],[k k],'g',[m m+1],[k k],'or');
hold on;
end
end
%linhas horizontais superiores
for k=a:b-1
for m=a:a+b-2
plot([m m+1],[k k],'g',[m m+1],[k k],'or');
hold on;
end
end
%linhas verticais do menor quadrado (esquerdo)
for k=0:a-2
for m=0:a-1
plot([m m],[k k+1],'g',[m m],[k k+1],'or');
5.2
end
Anexo
79
hold on;
end
%linhas verticais do maior quadrado (direito)
for k=0:b-2
for m=a:a+b-1
plot([m m],[k k+1],'g',[m m],[k k+1],'or');
hold on;
end
end
for x=0:b-1 plot([x x+a],[0 b-1],'g',[x x+a],[0 b-1],'or'); hold on;
end
for x=b:a+b-1 plot([x x-b],[0 a-1],'g',[x x-b],[0 a-1],'or'); hold
on; end
for y=0:a-1 plot([0 a+b-1],[y y+b-a],'g',[0 a+b-1],[y y+b-a],'or');
hold on; end
for y=a:b-1 plot([a a+b-1],[y y-a],'g',[a a+b-1],[y y-a],'or'); hold
on; end
end
gaussianoconverter
function[ ]=gaussianoconverter(a,b)
%Plota num plano bidimensional o grafo gaussiano com parâmetros a e b
%Restrição: 0<= a <=b
close all;
%linhas horizontais inferiores
for k=0:a-1
for m=0:a+b-2
A=converter([m k],[a b]);
B=converter([m+1 k],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
%linhas horizontais superiores
for k=a:b-1
for m=a:a+b-2
A=converter([m k],[a b]);
5.2
end
Anexo
end
80
B=converter([m+1 k],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
%linhas verticais do menor quadrado (esquerdo)
for k=0:a-2
for m=0:a-1
A=converter([m k],[a b]);
B=converter([m k+1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
%linhas verticais do maior quadrado (direito)
for k=0:b-2
for m=a:a+b-1
A=converter([m k],[a b]);
B=converter([m k+1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
for x=0:b-1
A=converter([x 0],[a b]);
B=converter([x+a b-1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
for x=b:a+b-1
A=converter([x 0],[a b]);
B=converter([x-b a-1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
for y=0:a-1
A=converter([0 y],[a b]);
B=converter([a+b-1 y+b-a],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
5.2
Anexo
81
end
for y=a:b-1
A=converter([a y],[a b]);
B=converter([a+b-1 y-a],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'b',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
Algoritmo para exibição de árvores geradoras independentes em RC-Grafos
GenParents([x(1)x(2)...x(m+1)], c, d, m) determina todos os pais do vértice [x(1)x(2)...x(m+
1)]d (na base d) em cada árvore geradora independente do grafo circulante com cXdm
vértices.
Função Principal:
GenParents
Funções Auxiliantes:
ShorstestPath
GenParents
function[]=GenParents(c,d,m)
%Parâmetros de entrada:
% c,d,m: valores que darão a quantidade de vértices do grafo N(V)=(cd^m)
% Parâmetros de saída:
% As saídas aparecem na seguinte sequência:
% - HPX (saltos que realmente aparecem no caminho P_x)
% - IPX (primeira linha da matriz I(P_x)
%
% Obs.: Para identificar cada árvore geradora, a primeira coluna fornece o
% sinal (1 para positivo e -1 para negativo) e a segunda coluna, o número
% da árvore. Na terceira coluna aparecem os pais correspondentes.
% Esta versão do GenParents desenhas as árvores geradoras
clc close all;
% Este 'for' inicializa o vetor X com 0's
q=0; % q é o número de vértices em que a busca por pais será feita
5.2
Anexo
82
for t=1:m+1
X(t)=0;
q=q+(d-1)*d^t;
end q=q-(m+1)*d;
% X(m+1 - (?)) resolve o problema de [0 0 1] ser trocado por [1 0 0]
r=0;
if c>d || c==d
r=q;
'c deve ser menor que d'
end
while(r<q) %'while' principal
r=r+1; % r é a variável que indicará quando o while será finalizado
X(m+1)=X(m+1)+1;
for i=0:m-1
if X(m+1-(i))==d
X(m+1-(i))=0;
X(m+1-(i+1))=X(m+1-(i+1))+1;
end
end
aux=r;
% Este 'for' calcula x (vértice)
x=0;
for i=0:m
x=x+ X(m+1-i)*d^(i); % x é calculado em valor inteiro (decimal)
end
% Calcula N (número de vértices do grafo) e arg é o ângulo usado
% nos desenhos das árvores geradoras
N=c*d^m; arg = (2*pi)/N;
% Este 'for' calcula o conjunto J (saltos)
for i=0:floor(log10(N)/log10(d)+1)-1
J(i+1)=d^i;
J(i+2+floor(log10(N)/log10(d)+1)-1)=-d^i;
end
if c>2
deltam=2*m+2;
end
if c==1 && d==2
deltam=2*m-1;
5.2
Anexo
83
end
if c==1 && d>2
deltam=2*m;
end
if c==2
deltam=2*m+1;
end
% Obtém HPX da função auxiliar "ShortestPath"
HPX=ShortestPath(X,c,d,m);
% tam é o tamanho do vetor HPX
tam=length(HPX);
%Calcula HPXBARRA em função de c
if c~=2
HPXBARRA=-HPX;
else
end
HPXBARRA=-HPX;
for i=1:length(HPXBARRA)-1
if HPXBARRA(i)==d^m || HPXBARRA(i)==-d^m
HPXBARRA(i)=HPXBARRA(length(HPXBARRA));
end
end
% Este 'for' calcula IPX, a primeira linha da matriz I(P_x)
for t=1:tam
min=HPX(t);
for k=t:tam
if abs(HPX(k))<min
min=HPX(K)
end
end
IPX(t)=min;
end
x
IPX
% Corresponde ao 'for' do algoritmo (parte 2)
for i=1:deltam
lambda(i)=-max(-(i-1),-(deltam-(i-1)-1));
% Os dois 'if' a seguir são a parte 3 do algoritmo
if i-1<lambda(i) || i-1==lambda(i)
5.2
Anexo
84
else
end
j=-d^(lambda(i));
sinal=-1;
i-1>lambda(i)
j=d^(lambda(i));
sinal=1;
V1=0;
%Variável auxiliar para verificar se j está em HPX
%V1=1 <=> j está em HPX
%V1=0 <=> j não está em HPX
V2=0;
%Variável auxiliar para verificar se j está em HPXBARRA
posj=0;
%Variável que será ulitizala pra ver a posição de j em IPX
%procura em qual posição de IPX j está
for k=1:tam
%tam = length(HPX) = length(IPX)
if j==IPX(k)
posj=k;
end
end
%Este 'if' elimina o problema de j poder estar
%na última posiçao indicando que seu sucessor
%estará na primeira posição
if posj==tam
posj=0;
end
for k=1:tam
if j==HPX(k)
V1=1;
end
end
if V1==1 % V1=1 significa que j pertence a HPX
A=x+IPX(posj+1);
if A < 0
A=x+IPX(posj+1)+N;
end
if A>=N
A=A-N;
end
5.2
Anexo
85
% Determinam qual árvore sera desenhada
fig=sinal*lambda(i)+deltam+3;
% + delta + 3 faz com que fig seja estritamente
%positivo e diferente de 1 e de 2 fig=1 e fig=2
%são reservados para a situação abaixo:
if sinal*lambda(i)==0
if sinal==1
fig=1;
end
end
if sinal==-1
fig=2;
end
figure(fig)
plot([cos(x*arg) cos(A*arg)],[sin(x*arg) sin(A*arg)],'k',
[cos(x*arg) cos(A*arg)],[sin(x*arg) sin(A*arg)],'ob');
hold on;
[sinal lambda(i) A]
else % Isto significa que V1=0, ou seja,j não pertence a HPX
for k=1:length(HPXBARRA)
if j==HPXBARRA(k)
V2=1;
end
end
if V2==1 % V2=1 significa que j pertence a HPXBARRA
A=x+j;
if A < 0
A=x+j+N;
end
if A>=N
A=A-N;
end
% Determinam qual árvore sera desenhada
fig=sinal*lambda(i)+deltam+3;
%+ delta + 3 faz com que fig seja estritamente
%positivo e diferente de 1 e de 2 fig=1 e fig=2
%são reservados para a situação abaixo:
if sinal*lambda(i)==0
if sinal==1
fig=1;
end
if sinal==-1
5.2
Anexo
86
end
end
fig=2;
figure(fig)
plot([cos(x*arg) cos(A*arg)],[sin(x*arg) sin(A*arg)],'k'
[cos(x*arg) cos(A*arg)],[sin(x*arg) sin(A*arg)],'ob');
hold on;
[sinal lambda(i) A]
else % V2=0(significa que j não pertence a HPXBARRA)
A=x-j;
if A < 0
A=x-j+N;
end
if A>=N
A=A-N;
end
% Determinam qual árvore será desenhada
fig=sinal*lambda(i)+deltam+3;
%+ delta + 3 faz com que fig seja estritamente
%positivo e diferente de 1 e de 2 fig=1 e fig=2
%são reservados para a situação abaixo:
if sinal*lambda(i)==0
if sinal==1
fig=1;
end
if sinal==-1
fig=2;
end
end
figure(fig)
plot([cos(x*arg) cos(A*arg)], [sin(x*arg) sin(A*arg)],'k',
[cos(x*arg) cos(A*arg)], [sin(x*arg) sin(A*arg)],'ob');
hold on;
[sinal lambda(i) A]
end
end
end %finaliza o for
%Este if evita que o programa procure os pais do último vértice que é
%congruente ao vértice 0. Estes pais não existem.
%Este é o momento que o loop termina
if x==c*d^m-1
5.2
Anexo
87
r=q; %isto força a parada do while
end
end %finaliza o while principal
%Este if faz com que o programa exiba deltam quando ele realmente for
%calculado. Caso c>=d, o programa não entra no 'while'.
if c<d
deltam
end
end %finaliza o programa
ShortestPath
function[HPX]=ShortestPath(X,c,d,m)
%X=[ 1 ... m-1 m
m+1] <-> X=[x_m ... x_2 x_1
x_0]
Carry=0; N= c*d^m; z=0; P=0;
for i=0:m-1
if (0 < X(m+1-i) && X(m+1-i) <= floor(d/2))
z=z+1;
HPX(z)=-d^i;
%nHPX(z)=X(m+1-i);
Carry = 0;
else
if (floor(d/2) < X(m+1-i) && X(m+1-i) <= d-1)
z=z+1;
HPX(z)=+d^i;
%nHPX(z)=d-X(m+1-i);
X(m+1-i-1) = X(m+1-i-1) + 1;
Carry = 1;
else
if Carry==1
X(m+1-i-1) = X(m+1-i-1) + 1;
end
end
end
end
%obs.: X(1) = x_m
if (c>=2 && 0 < X(1) && X(1) <= floor(c/2))
z=z+1;
HPX(z)=-d^m;
5.2
Anexo
else
end
88
%nHPX(z)=X(1);
if (c>2 && floor(c/2) < X(1) && X(1) <= c-1)
z=z+1;
HPX(z)=+d^m;
%nHPX(z)=c-X(1);
end
end
Algoritmo para exibição de árvores geradoras independentes em Grafos Gaussianos
Este programa gera árvores geradoras em grafos gaussianos. O comando arvore([ab])
faz com o que o program execute e busque 4 árvores geradoras para o grafo gaussiano,
exibidas em 4 guras na topologia losangular.
Função Principal:
arvore
Funções Auxiliantes:
adjacencias, caminhos, converter, converterporiginal,
disjuntos, gaussianoconverter, plotaadjacentes
arvore
function[]=arvore(w)
%w=[a b] : graph generator
clc close all a=w(1); b=w(2);
N=a^2+b^2; %numero de vertices do grafo
L=[0 0]; %L será um vetor que armazenara a lista dos vertices a serem
%varridos pelo programa
ltam=0; %ltam é o tamanho do vetor L utilizado
L2=[0 0]; %L2 é uma lista temporaria de auxilio a L
ltam2=0; %ltam é o tamanho do vetor L2 utilizado
%V é uma matriz que armazenara todos vertices ja visitados no grafo
%size(V) = Vtam (linhas) x 2 (colunas)
V(1,1)=0; V(1,2)=0; V(1,:)=[0 0];
%Vtam é o número de linhas da matriz V
Vtam=1;
M=adjacencias(w); %Coloca em M a matriz de adjacencias
5.2
Anexo
89
gaussianoconverter(a,b); %desenha o grafo gaussiano na topologia losangular
hold on;
u=converter([0 -1],w); %Vértice imediamente abaixo do 0+0i na topologia losangula
V(2,:)=u; Vtam=2; plot([0 u(1)],[0 u(2)],'k',[0 u(1)],[0
u(2)],'ok'); hold on; A1=[0 0 u(1) u(2)]; L=[u(1) u(2)]; ltam=2;
[Vtam,V,L,L2,ltam2,A1]=plotaadjacentes(u,N,M,Vtam,V,L,L2,A1);
L=L2; %Passou os dados de L2 para L
clear L2; clear ltam2 L2=[0 0]; for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A1]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A1);
end
for cont=1:10
L=L2;
clear L2
clear ltam2
L2=[0 0];
for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A1]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A1)
end
end
s=size(A1); for i=1:s
v=converterporiginal([A1(i,1) A1(i,2)],[a b]);
A1(i,5)=v(1); A1(i,6)=v(2);
v=converterporiginal([A1(i,3) A1(i,4)],[a b]);
A1(i,7)=v(1); A1(i,8)=v(2);
end
A1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2)
L=[0 0]; ltam=0; L2=[0 0]; ltam2=0; clear V; V(1,1)=0; V(1,2)=0;
V(1,:)=[0 0]; Vtam=1;
gaussianoconverter(a,b); %desenha o grafo gaussiano na topologia losangular
hold on;
5.2
Anexo
90
u=converter([-1 0],w); %Vértice imediamente abaixo do 0+0i na topologia losangula
V(2,:)=u; Vtam=2; plot([0 u(1)],[0 u(2)],'k',[0 u(1)],[0
u(2)],'ok'); hold on; A2=[0 0 u(1) u(2)]; L=[u(1) u(2)]; ltam=2;
[Vtam,V,L,L2,ltam2,A2]=plotaadjacentes(u,N,M,Vtam,V,L,L2,A2);
L=L2; %Passou os dados de L2 para L
clear L2; clear ltam2 L2=[0 0]; for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A2]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A2);
end
for cont=1:10
L=L2;
clear L2
clear ltam2
L2=[0 0];
for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A2]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A2)
end
end
s=size(A2); for i=1:s
v=converterporiginal([A2(i,1) A2(i,2)],[a b]);
A2(i,5)=v(1); A2(i,6)=v(2);
v=converterporiginal([A2(i,3) A2(i,4)],[a b]);
A2(i,7)=v(1); A2(i,8)=v(2);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(3)
L=[0 0]; ltam=0; L2=[0 0]; ltam2=0; clear V; V(1,1)=0; V(1,2)=0;
V(1,:)=[0 0]; Vtam=1;
gaussianoconverter(a,b); %desenha o grafo gaussiano na topologia losangular
hold on;
u=converter([0 1],w); %Vértice imediamente abaixo do 0+0i na topologia losangular
V(2,:)=u; Vtam=2; plot([0 u(1)],[0 u(2)],'k',[0 u(1)],[0
u(2)],'ok'); hold on; A3=[0 0 u(1) u(2)]; L=[u(1) u(2)]; ltam=2;
5.2
Anexo
91
[Vtam,V,L,L2,ltam2,A3]=plotaadjacentes(u,N,M,Vtam,V,L,L2,A3);
L=L2; %Passou os dados de L2 para L
clear L2; clear ltam2 L2=[0 0]; for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A3]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A3);
end
for cont=1:10
L=L2;
clear L2
clear ltam2
L2=[0 0];
for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A3]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A3)
end
end
s=size(A3); for i=1:s
v=converterporiginal([A3(i,1) A3(i,2)],[a b]);
A3(i,5)=v(1); A3(i,6)=v(2);
v=converterporiginal([A3(i,3) A3(i,4)],[a b]);
A3(i,7)=v(1); A3(i,8)=v(2);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(4)
L=[0 0]; ltam=0; L2=[0 0]; ltam2=0; clear V; V(1,1)=0; V(1,2)=0;
V(1,:)=[0 0]; Vtam=1;
gaussianoconverter(a,b); %desenha o grafo gaussiano na topologia losangular
hold on;
u=converter([1 0],w); %Vértice imediamente abaixo do 0+0i na topologia losangular
V(2,:)=u; Vtam=2; plot([0 u(1)],[0 u(2)],'k',[0 u(1)],[0
u(2)],'ok'); hold on; A4=[0 0 u(1) u(2)]; L=[u(1) u(2)]; ltam=2;
[Vtam,V,L,L2,ltam2,A4]=plotaadjacentes(u,N,M,Vtam,V,L,L2,A4);
L=L2; %Passou os dados de L2 para L
clear L2; clear ltam2 L2=[0 0]; for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A4]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A4);
end
5.2
Anexo
92
for cont=1:10
L=L2;
clear L2
clear ltam2
L2=[0 0];
for n=2:length(L)/2 -1
[Vtam,V,L,L2,ltam2,A4]=plotaadjacentes([L(2*n-1) L(2*n)],N,M,Vtam,V,L,L2,A4)
end
end
s=size(A4); for i=1:s
v=converterporiginal([A4(i,1) A4(i,2)],[a b]);
A4(i,5)=v(1); A4(i,6)=v(2);
v=converterporiginal([A4(i,3) A4(i,4)],[a b]);
A4(i,7)=v(1); A4(i,8)=v(2);
end
C1=caminhos(A1,w); C2=caminhos(A2,w); C3=caminhos(A3,w);
C4=caminhos(A4,w);
C1 C2 C3 C4
%disj=disjuntos(C1,C2)
if disjuntos(C1,C2)==1
'A1 e A2 são disjuntos'
end if disjuntos(C1,C3)==1
'A1 e A3 são disjuntos'
end if disjuntos(C1,C4)==1
'A1 e A4 são disjuntos'
end if disjuntos(C2,C3)==1
'A2 e A3 são disjuntos'
end if disjuntos(C2,C4)==1
'A2 e A4 são disjuntos'
end if disjuntos(C3,C4)==1
'A3 e A4 são disjuntos'
end
end
adjacencias
function[M]=adjacencias(w) a=w(1); b=w(2); line=0;
5.2
Anexo
N=a^2+b^2; for i=0:a+b-1
for j=0:a-1
line=line+1;
c=converter([i j],w);
M(line,1)=c(1);
M(line,2)=c(2);
c=converter([i-1 j],w);
M(line,3)=c(1);
M(line,4)=c(2);
c=converter([i j+1],w);
M(line,5)=c(1);
M(line,6)=c(2);
c=converter([i+1 j],w);
M(line,7)=c(1);
M(line,8)=c(2);
c=converter([i j-1],w);
M(line,9)=c(1);
M(line,10)=c(2);
end
end
for i=a:a+b-1
for j=a:b-1
line=line+1;
c=converter([i j],w);
M(line,1)=c(1);
M(line,2)=c(2);
c=converter([i-1 j],w);
M(line,3)=c(1);
M(line,4)=c(2);
c=converter([i j+1],w);
M(line,5)=c(1);
M(line,6)=c(2);
c=converter([i+1 j],w);
M(line,7)=c(1);
M(line,8)=c(2);
c=converter([i j-1],w);
M(line,9)=c(1);
M(line,10)=c(2);
end
end
end
93
5.2
Anexo
94
caminhos
function[C]=caminhos(A,w)
%Esta função tem como resultado uma matriz com todos os caminhos na
%árvore geradora representada por A
%k fornece a posição da matriz C (colunas de C)
d=0; %d fornece a posição da matriz C (linha de C)
s=size(A);
linhas=s(1); %número de linhas da matriz A
sair=0;
for i=0:w(1)+w(2)-1
for j=0:w(1)-1
itemp=i;
jtemp=j;
d=d+1;
k=1;
C(d,2*k-1)=itemp;
C(d,2*k)=jtemp;
k=k+1;
while(sair==0)
for lin=1:linhas
if A(lin,7)==itemp && A(lin,8)==jtemp
C(d,2*k-1)=A(lin,5);
itemp=A(lin,5);
C(d,2*k)=A(lin,6);
jtemp=A(lin,6);
k=k+1;
end
end
if itemp==0 && jtemp==0
sair=1;
end
end
end
end
sair=0;
5.2
Anexo
95
sair=0;
for i=w(1):w(1)+w(2)-1
for j=w(1):w(2)-1
itemp=i;
jtemp=j;
d=d+1;
k=1;
C(d,2*k-1)=itemp;
C(d,2*k)=jtemp;
k=k+1;
while(itemp~=0 && jtemp~=0)
for lin=1:linhas
if A(lin,7)==itemp && A(lin,8)==jtemp
C(d,2*k-1)=A(lin,5);
itemp=A(lin,5);
C(d,2*k)=A(lin,6);
jtemp=A(lin,6);
k=k+1;
end
end
if itemp==0 && jtemp==0
sair=1;
end
end
end
end
sair=0;
end
converter
function[D]=converter(alpha,gerador)
%Converte o elemento alpha em G_gerador para o elemento que possui a
%menor norma dentro da sua classe de equivalência.
%gerador = a+bi (gerador do grafo)
%alpha = c+di (elemento a ser convertido)
a=gerador(1); b=gerador(2); c=alpha(1); d=alpha(2); N=a^2+b^2;
D(1)=real(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i));
5.2
Anexo
96
D(2)=imag(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i)); end
converterporiginal
function[R]=converterporiginal(alpha,gerador)
%Converte o elemento alpha em G_gerador para o elemento que possui a
%menor norma dentro da sua classe de equivalência.
%gerador = a+bi (gerador do grafo)
%alpha = c+di (elemento a ser convertido)
a=gerador(1); b=gerador(2); c=alpha(1); d=alpha(2); N=a^2+b^2;
D(1)=real(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i));
D(2)=imag(c+d*i-round((c+d*i)*(a-b*i)/N)*(a+b*i));
% if norm(D)==norm(alpha)
%
D=alpha;
% end
R=D;
if (D(2)>=a)
R(2)=D(2)-a;
R(1)=D(1)+b;
%'cond 1';
end
if ((D(1)<0) && (D(2)<a))
if D(2)>-(b-a+1)
R(1)=D(1)+a+b;
R(2)=D(2)+b-a;
%'cond 2';
end
if D(2)<-(b-a)
R(1)=D(1)+a;
R(2)=D(2)+b;
%'cond 3 part1';
end
end
if ((D(1)>=0) && (D(2)<0))
R(1)=D(1)+a;
R(2)=D(2)+b;
%'cond 3 part2'
end
end
5.2
Anexo
97
disjuntos
function[disj]=disjuntos(C,D)
%verifica se duas arvores são disjuntas, usando suas matrizes de caminhos
%Retorna disj=1 se forem disjuntos e disj=0 se nao forem.
disj=1; s=size(C); t=size(D);
%verifica se as matrizes tem tamanhos diferentes. Caso positivo, completa
%a menor com zeros para ficar com o mesmo tamanho da maior
if s(2)~=t(2)
if s(2)>t(2)
for int=s(2)-(s(2)-t(2))+1:s(2)
for int2=2:s(1)
D(int2,int)=0;
end
end
end
if t(2)>s(2)
for int=t(2)-(t(2)-s(2))+1:t(2)
for int2=2:s(1)
C(int2,int)=0;
end
end
end
end
sairdowhileprincipal=0; sair2=0; for lin=2:s(1)
k=1;
while(sairdowhileprincipal==0)
k=k+1;
m=2;
itemp = C(lin,2*k-1);
jtemp = C(lin,2*k);
if itemp==0 && jtemp==0
sairdowhileprincipal=1;
sair2=1;
5.2
Anexo
98
end
while(sair2==0)
if itemp==D(lin,2*m-1) && jtemp==D(lin,2*m)
if itemp~=0 || jtemp~=0
disj=0;
sair2=1;
sairdowhileprincipal=1;
end
end
if D(lin,2*m-1)==0 && D(lin,2*m)==0
sair2=1;
end
m=m+1;
end
sair2=0;
end
sairdowhileprincipal=0;
if disj==0
sairdowhileprincipal=1;
end
end
end
gaussianoconverter
function[ ]=gaussianoconverter(a,b)
%Plota num plano bidimensional o grafo gaussiano com parâmetros a e b
%Restrição: 0<= a <=b
close all;
%linhas horizontais inferiores
for k=0:a-1
for m=0:a+b-2
A=converter([m k],[a b]);
B=converter([m+1 k],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
5.2
Anexo
99
end
%linhas horizontais superiores
for k=a:b-1
for m=a:a+b-2
A=converter([m k],[a b]);
B=converter([m+1 k],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
%linhas verticais do menor quadrado (esquerdo)
for k=0:a-2
for m=0:a-1
A=converter([m k],[a b]);
B=converter([m k+1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
%linhas verticais do maior quadrado (direito)
for k=0:b-2
for m=a:a+b-1
A=converter([m k],[a b]);
B=converter([m k+1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
for x=0:b-1
A=converter([x 0],[a b]);
B=converter([x+a b-1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
for x=b:a+b-1
A=converter([x 0],[a b]);
B=converter([x-b a-1],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
5.2
Anexo
100
for y=0:a-1
A=converter([0 y],[a b]);
B=converter([a+b-1 y+b-a],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
for y=a:b-1
A=converter([a y],[a b]);
B=converter([a+b-1 y-a],[a b]);
plot([A(1) B(1)],[A(2) B(2)],'y',[A(1) B(1)],[A(2) B(2)],'or');
hold on;
end
end
plotaadjacentes
function[Vtam,V,L,L2,ltam2,A]=plotaadjacentes(u,N,M,Vtam,V,L,L2,A)
s=size(A); Atam=s(1);
ltam2=length(L2); for i=1:N
if u(1)==M(i,1) && u(2)==M(i,2)
verifica=1;
for j=1:Vtam
if V(j,1)==M(i,3) && V(j,2)==M(i,4)
verifica=0;
end
end
if verifica==1
plot([u(1) M(i,3)],[u(2) M(i,4)],'k',[u(1) M(i,3)],[u(2) M(i,4)],'ok')
hold on;
A(Atam+1,:)=[u(1) u(2) M(i,3) M(i,4)];
Atam=Atam+1;
L2(ltam2+1)=M(i,3);
L2(ltam2+2)=M(i,4);
ltam2=ltam2+2;
V(Vtam+1,:)=[M(i,3) M(i,4)];
Vtam=Vtam+1;
end
5.2
Anexo
101
verifica=1;
for j=1:Vtam
if V(j,1)==M(i,5) && V(j,2)==M(i,6)
verifica=0;
end
end
if verifica==1
plot([u(1) M(i,5)],[u(2) M(i,6)],'k',[u(1) M(i,5)],[u(2) M(i,6)],'ok');
hold on;
A(Atam+1,:)=[u(1) u(2) M(i,5) M(i,6)];
Atam=Atam+1;
L2(ltam2+1)=M(i,5);
L2(ltam2+2)=M(i,6);
ltam2=ltam2+2;
V(Vtam+1,:)=[M(i,5) M(i,6)];
Vtam=Vtam+1;
end
verifica=1;
for j=1:Vtam
if V(j,1)==M(i,7) && V(j,2)==M(i,8)
verifica=0;
end
end
if verifica==1
plot([u(1) M(i,7)],[u(2) M(i,8)],'k',[u(1) M(i,7)],[u(2) M(i,8)],'ok');
hold on;
A(Atam+1,:)=[u(1) u(2) M(i,7) M(i,8)];
Atam=Atam+1;
L2(ltam2+1)=M(i,7);
L2(ltam2+2)=M(i,8);
ltam2=ltam2+2;
V(Vtam+1,:)=[M(i,7) M(i,8)];
Vtam=Vtam+1;
end
verifica=1;
for j=1:Vtam
if V(j,1)==M(i,9) && V(j,2)==M(i,10)
verifica=0;
end
.0
Anexo
102
end
if verifica==1
plot([u(1) M(i,9)],[u(2) M(i,10)],'k',[u(1) M(i,9)],[u(2) M(i,10)],'ok'
hold on;
A(Atam+1,:)=[u(1) u(2) M(i,9) M(i,10)];
Atam=Atam+1;
L2(ltam2+1)=M(i,9);
L2(ltam2+2)=M(i,10);
ltam2=ltam2+2;
V(Vtam+1,:)=[M(i,9) M(i,10)];
Vtam=Vtam+1;
end
end
end
ltam2=length(L2);
end