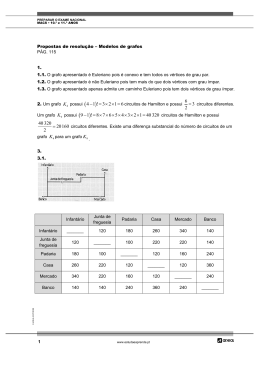
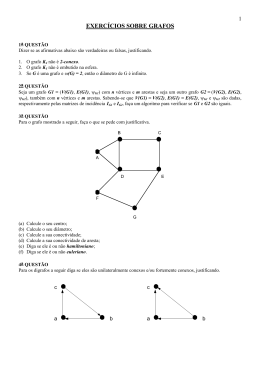
Teoria dos Grafos
Implementação de Grafos
Basicamente existem três estruturas de dados propícias para representar grafos:
Matriz de Adjacente
Lista Adjacente
Matriz Incidência
1 Matriz Adjacência
Uma matriz Adjacente é uma matriz tal que:
M(i, j) = 1
M(i, j) = 0
se a aresta (i,j) existe
senão existe arco (i,j)
Onde i e j são vértices do grafo
GRAFO
REPRESENTAÇÃO
Em caso de grafos orientado tem-se:
Se NÃO existe a aresta (i,j) entre dois vértices i e j então M(i, j) = 0
Se existe a aresta orientada (i,j) entre dois vértices i e j então M(i, j) = 1
Se existe a aresta orientada (j,i) entre dois vértices j e i então M(j, i) = -1
Exemplo:
GRAFO
Nota de Aula
Sidney Vieira
REPRESENTAÇÃO
1
Em caso de grafos valorados tem-se:
Se NÃO existe a aresta (i,j) entre dois vértices i e j então M(i, j) = 0
Se existe a aresta valorada (i,j) entre dois vértices i e j então M(i, j) = valor
de i a j
Exemplo:
Grafo
Representação
1
2
3
4
1
2
3
4
0
0
0
0
30
0
5
0
0
0
0
0
20
10
0
0
2 Listas de adjacência
Nesta representação emprega-se a estrutura de lista de modo que as n linhas da
matriz de adjacência são representadas como n listas encadeadas. Existe uma lista para
cada vértice em G. Os nós na lista i representam os vértices que são adjacentes ao
vértice i.
Cada nó na lista possui pelo menos dois campos:
VÉRTICE → armazena o indice do vértice que é adjacente i
NEXT → um ponteiro para o próximo nó adjacente.
As cabeças das listas podem ser armazenas em um array de ponteiros para
facilitar o acesso aos vértices.
Nota de Aula
Sidney Vieira
2
Exemplo:
GRAFO
REPRESENTAÇÃO
3 Matriz de incidência
Sendo
G(V,A) um grafo de n vértices v1, v2... vn, e m arestas a1, a2...am, e
nenhum laço.
Uma matriz de incidência é uma matriz n x m, onde o valor de cada elemento ejk
da matriz é determinado da seguinte maneira:
M(i, j) = 1
M(i, j) = 0
se a aresta ak é incidente ao vértice aj
caso contrário
Exemplo:
GRAFO
REPRESENTAÇÃO
a1 a2 a3 a4 a5 a6 a7 a8
Nota de Aula
Sidney Vieira
v1 0
0
0
1
0
1
0
0
v2 0
0
0
0
1
1
1
1
v3 0
0
0
0
0
0
0
1
v4 1
1
1
0
1
0
0
0
v5 0
0
1
1
0
0
1
0
v6 1
1
0
0
0
0
0
0
3
Propriedades da matriz de incidência:
•
•
•
•
Como cada aresta é incidente a exatamente dois vértices, cada coluna contém
exatamente dois 1.
O número de 1 em cada linha é igual ao grau do vértice correspondente.
Uma linha que contém somente 0 representa um vértice isolado.
Arestas paralelas resultam em duas colunas idênticas.
4 Alguns Algoritmos de implementação:
4.1 Grau de um Vértice
para i <-- 1 até N, faça
grau <-- 0
para j <-- 1 até N, faça
se matriz[i][j] = 1, então
grau <-- grau + 1
fim-se
fim-para
imprima "O vértice " i " tem grau " grau "."
fim-para
4.2 Matriz de Adjacências
para i
1 até N, faça
para j <-- 1 até N, faça
matriz[i][j] <-- 0
fim-para
fim-para
enquanto (recebe x, y e x <-- 0), faça
matriz[x][y] <-- 1
matriz[y][x] <-- 1
fim-enquanto
4.3 Lista de Adjacências
para i
1 até N, faça
grau[i] <-- 0
fim-para
enquanto (recebe x, y e x != 0), faça
lista[x][grau[x]++] <-- y
Nota de Aula
Sidney Vieira
4
lista[y][grau[y]++] <-- x
fim-enquanto
4.4 Lista de Adjacências junto com Matriz de Adjacências
para i
1 até N, faça
para j <-- 1 até N, faça
matriz[i][j] <-- 0
fim-para
grau[i] <-- 0
fim-para
enquanto (recebe x, y e x != 0), faça
matriz[x][y] <-- 1
matriz[y][x] <-- 1
lista[x][grau[x]++] <-- y
lista[y][grau[y]++] <-- x
fim-enquanto
Nota de Aula
Sidney Vieira
5