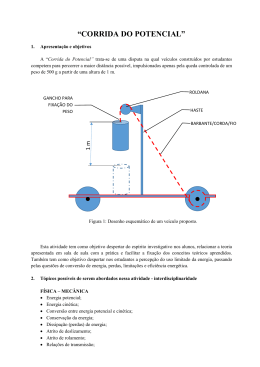
1. (Coolidge)
No arranjo experimental da figura, os corpos A e B têm massas,
respectivamente, iguais a 2,0 kg e 3,0 kg. Despreze atritos e as
massas do fio e da polia. Adote g = 10,0 m/s£.
Considerando que os corpos são abandonados em repouso,
calcule os trabalhos realizados pelos pesos dos corpos A e B
sobre os respectivos corpos durante o primeiro segundo de
movimento.
4. (Fuvest) Um carro de corrida, com massa total m = 800 kg,
parte do repouso e, com aceleração constante, atinge, após 15
segundos, a velocidade de 270 km/h (ou seja 75 m/s). A figura
representa o velocímetro, que indica a velocidade instantânea
do carro. Despreze as perdas por atrito e as energias cinéticas
de rotação (como a das rodas do carro). Suponha que o
movimento ocorre numa trajetória retilínea e horizontal.
a) Qual a velocidade angular Ÿ do ponteiro do velocímetro
durante a aceleração do carro? Indique a unidade usada.
b) Qual o valor do módulo da aceleração do carro nesses 15
segundos?
c) Qual o valor da componente horizontal da força que a pista
aplica ao carro durante sua aceleração?
d) Qual a potência fornecida pelo motor quando o carro está a
180 km/h?
2. (Unicamp) Sob a ação de uma força constante, um corpo de
massa m = 4,0 kg adquire, a partir do repouso, a velocidade de
10 m/s.
a) Qual é o trabalho realizado por essa força?
b) Se o corpo se deslocou 25 m, qual o valor da força aplicada?
3. (Unesp) Um fruto de 0,10 kg, inicialmente em repouso,
desprendeu-se de uma árvore à beira de um penhasco e caiu 55
m, esborrachando-se numa rocha. Se a velocidade
imediatamente antes do impacto com a rocha era 30 m/s e a
aceleração da gravidade local vale 10 m/s£, calcule as
quantidades de energia mecânica dissipadas:
a) na interação do fruto com a rocha, ao se esborrachar;
b) na interação do fruto com o ar, durante a queda.
5. (Unesp) Certa máquina M• eleva verticalmente um corpo de
massa m• = 1,0 kg a 20,0 m de altura em 10,0 s, em movimento
uniforme. Outra máquina M‚ acelera em uma superfície
horizontal, sem atrito, um corpo de massa m‚ = 3,0 kg, desde o
repouso até a velocidade de 10,0 m/s, em 2,0 s.
a) De quanto foi o trabalho realizado por cada uma das
máquinas?
b) Qual a potência média desenvolvida por cada máquina?
6. (Unicamp) Um carro recentemente lançado pela indústria
brasileira tem aproximadamente 1500 kg e pode acelerar, do
repouso até uma velocidade de 108 km/h, em 10 segundos.
(fonte: "Revista Quatro Rodas", agosto/92).
Adote 1 cavalo-vapor (CV) = 750 W.
a) Qual o trabalho realizado nesta aceleração?
b) Qual a potência do carro em CV?
7. (Fuvest-gv) Na figura a seguir, tem-se uma mola de massa
desprezível e constante elástica 200 N/m, comprimida de 20 cm
entre uma parede e um carrinho de 2,0 kg. Quando o carrinho é
solto, toda a energia mecânica da mola é transferida ao mesmo.
Desprezando-se o atrito, pede-se:
9. (Uepg) Com base na figura a seguir, calcule a menor
velocidade com que o corpo deve passar pelo ponto A para ser
capaz de atingir o ponto B. Despreze o atrito e considere g = 10
m/s£.
a) nas condições indicadas na figura, o valor da força que a
mola exerce na parede.
b) a velocidade com que o carrinho se desloca, quando se
desprende da mola.
10. (Ufpe) Um pequeno bloco, de massa m = 0,5 kg, inicialmente
em repouso no ponto A, é largado de uma altura h = 0,8 m. O
bloco desliza, sem atrito, ao longo de uma superfície e colide
com um outro bloco, de mesma massa, inicialmente em repouso
no ponto B (veja a figura a seguir). Determine a velocidade dos
blocos após a colisão, em m/s, considerando-a perfeitamente
inelástica.
8. (G1) Uma esquiadora, de massa 50 kg, percorre as trajetórias
I, II e III, partindo do repouso e do mesmo ponto.
Despreze os atritos, a resistência do ar e adote g = 10 m/s£.
a) Qual o trabalho realizado pela força peso da esquiadora em
cada trajeto?
b) Compare a potência desenvolvida pela esquiadora, ao passar
pelos pontos A, B e C, sabendo que, nesses pontos, sua
velocidade tem a mesma direção.
11. (Unesp) Um pássaro de massa igual a 1,0 kg, inicialmente
em repouso no solo, alça vôo numa atmosfera isotrópica.
Sempre batendo asas, ele mantém velocidade escalar constante
de 10 m/s e atinge 20 m de altura, consumindo 75,0 calorias
com os movimentos de seus músculos. Determine a energia
dissipada pela resistência do ar.
Considere: 1 cal ¸ 4 J e g = 10 m/s£.
12. (Unesp) Um atleta, com massa de 80 kg, salta de uma altura
de 3,2 m sobre uma cama elástica, atingindo exatamente o
centro da cama, em postura ereta, como ilustrado na figura.
Devido à sua interação com a cama, ele é lançado novamente
para o alto, também em postura ereta, até a altura de 2,45 m
acima da posição em que a cama se encontrava. Considerando
que o lançamento se deve exclusivamente à força de restituição
da cama elástica e que a interação do atleta com a cama durou
0,4 s, calcule o valor médio da força que a cama aplica ao atleta.
Considere g = 10 m/s£
13. (Unesp) Um tubo de massa M contendo uma gota de éter
(de massa desprezível) é suspenso por meio de um fio leve de
comprimento L, conforme ilustrado na figura a seguir. Mostre
que (M/m)Ë(2gL) é a velocidade horizontal mínima com que a
rolha de massa m deve sair do tubo aquecido para que ele atinja
a altura de seu ponto de suspensão (g é a aceleração da
gravidade).
14. (Unesp) Para medir a velocidade de uma bala, preparou-se
um bloco de madeira de 0,990 kg, que foi colocado a 0,80 m do
solo, sobre uma mesa plana, horizontal e perfeitamente lisa,
como mostra a figura adiante. A bala, disparada horizontalmente
contra o bloco em repouso, alojou-se nele, e o conjunto (bala +
bloco) foi lançado com velocidade V, atingindo o solo a 1,20 m
da borda da mesa.
a) Adotando g = 10 m/s£, determine a velocidade V do conjunto,
ao abandonar a mesa. (Despreze a resistência e o empuxo do
ar.)
b) Determine a velocidade com que a bala atingiu o bloco,
sabendo-se que sua massa é igual a 0,010 kg.
15. (Unesp) Um bloco de massa 0,20 kg e outro de massa 0,60
kg, unidos por um elástico de massa desprezível e inicialmente
esticado, são mantidos em repouso sobre uma superfície plana,
horizontal e perfeitamente lisa. Se os blocos forem liberados
simultaneamente, verifica-se que adquirem, depois que o
elástico fica relaxado, velocidades iguais a 3,0 m/s e 1,0 m/s,
respectivamente.
a) Qual era a energia armazenada no elástico (energia potencial
elástica), enquanto os blocos estavam sendo mantidos em
repouso?
b) Se apenas o bloco de massa 0,60 kg tivesse sido liberado,
que velocidade teria alcançado, depois que o elástico ficasse
relaxado?
16. (Unicamp) Um carrinho, de massa m• = 80 kg, desloca-se
horizontalmente com velocidade v• = 5 m/s. Um bloco de massa
m‚ = 20 kg cai verticalmente sobre o carrinho, de uma altura
muito pequena, aderindo a ele.
a) Com que velocidade final move-se o conjunto?
b) Que quantidade de energia mecânica foi transformada em
energia térmica?
17. (Ufg) Um bloco de massa m, abandonado de uma altura h,
desliza sem atrito até chocar-se elasticamente com outro bloco
de massa 2m em repouso, conforme figura a seguir.
Após esta colisão, o segundo bloco percorre o trecho BC, onde
há atrito, alcançando uma altura
2h/9. Com base no exposto, calcule:
a) A velocidade dos blocos imediatamente após o choque.
b) A energia dissipada pelo atrito.
18. (Fuvest) Adote: calor específico da água = 4 J/g°C
A figura adiante esquematiza o arranjo utilizado em uma
repetição da experiência de Joule. O calorímetro utilizado, com
capacidade térmica de 1600 J/°C, continha 200 g de água a uma
temperatura inicial de 22,00 °C. O corpo de massa M = 1,5 kg, é
abandonado de uma altura de 8 m. O procedimento foi repetido
6 vezes até que a temperatura do conjunto água + calorímetro
atingisse 22,20 °C.
a) Calcule a quantidade de calor necessária para aumentar a
temperatura do conjunto água + calorímetro.
b) Do total da energia mecânica liberada nas 6 quedas do corpo,
qual a fração utilizada para aquecer o conjunto?
19. (Ufpel) Analise a afirmativa a seguir:
Em uma colisão entre um carro e uma moto, ambos em
movimento e na mesma estrada, mas em sentidos contrários,
observou-se que após a colisão a moto foi jogada a uma
distância maior do que a do carro.
Baseado em seus conhecimentos sobre mecânica e na análise
da situação descrita acima, bem como no fato de que os corpos
não se deformam durante a colisão, é correto afirmar que,
durante a mesma,
a) a força de ação é menor do que a força de reação, fazendo
com que a aceleração da moto seja maior que a do carro, após
a colisão, já que a moto possui menor massa.
b) a força de ação é maior do que a força de reação, fazendo
com que a aceleração da moto seja maior que a do carro, após
a colisão, já que a moto possui menor massa.
c) as forças de ação e reação apresentam iguais intensidades,
fazendo com que a aceleração da moto seja maior que a do
carro, após a colisão, já que a moto possui menor massa.
d) a força de ação é menor do que a força de reação, porém a
aceleração da moto, após a colisão, depende das velocidades
do carro e da moto imediatamente anteriores a colisão.
e) exercerá maior força sobre o outro aquele que tiver maior
massa e, portanto, irá adquirir menor aceleração após a colisão.
20. (Fei) Um corpo de massa 5 kg é retirado de um ponto A e
levado para um ponto B, distante 40 m na horizontal e 30 m na
vertical traçadas a partir do ponto A. Qual é o módulo do
trabalho realizado pela força peso?
a) 2500 J
b) 2000 J
c) 900 J
d) 500 J
e) 1500 J
23. (Ufu) Um avião de massa 4000 kg está com uma velocidade
horizontal constante de 50 m/s e a uma altura inicial de 20 m
(situação A da figura a seguir). A partir dessa posição, o avião
desce com uma velocidade vertical constante, mantendo a
velocidade horizontal inalterada e toca a pista, após percorrer
uma distância horizontal de 200 metros (situação B do desenho
a seguir).
21. (Fuvest) Um pai de 70 kg e seu filho de 50 kg pedalam lado
a lado, em bicicletas idênticas, mantendo sempre velocidade
uniforme. Se ambos sobem uma rampa e atingem um patamar
plano, podemos afirmar que, na subida da rampa até atingir o
patamar, o filho, em relação ao pai:
a) realizou mais trabalho.
b) realizou a mesma quantidade de trabalho.
c) possuía mais energia cinética.
d) possuía a mesma quantidade de energia cinética.
e) desenvolveu potência mecânica menor.
22. (Uel) Um corpo de massa 2,0 kg é arrastado sobre uma
superfície horizontal com velocidade constante de 5,0 m/s,
durante 10 s. Sobre esse movimento são feitas as afirmações:
I. o trabalho realizado pela força peso do corpo é nulo.
II. o trabalho realizado pela força de atrito é nulo.
III. o trabalho realizado pela força resultante é nulo.
Dessas afirmações, SOMENTE
a) I e III são corretas.
b) I e II são corretas.
c) III é correta.
d) II é correta.
e) I é correta.
Logo após tocar o solo, é aplicada uma aceleração constante ao
avião para freá-lo. O avião dispõe de 1 km de pista para parar
completamente.
Com base nessas informações, marque a alternativa correta.
a) Para que o avião pare em segurança, sua aceleração mínima
no solo deverá ser de 1,25 m/s£.
b) A velocidade vertical do avião durante a descida deve ser de
10 m/s.
c) Durante a descida, a energia potencial gravitacional do avião
será convertida em energia cinética.
d) O trabalho realizado para frear completamente o avião
dependerá de onde ele irá parar.
24. (Unitau) Uma partícula de massa m = 10 g se move no plano
x, y com uma velocidade tal que sua componente, ao longo do
eixo x, é de 4,0 m/s e, ao longo do eixo y, é de 2,0 m/s. Nessas
condições, pode-se afirmar que sua energia cinética vale:
a) 0,10 J.
b) 0,18 J.
c) 100 J.
d) 180 J.
e) 190 J.
25. (Fuvest) Um corpo de massa m é solto no ponto A de uma
superfície e desliza, sem atrito, até atingir o ponto B. A partir
deste ponto o corpo desloca-se numa superfície horizontal com
atrito, até parar no ponto C, a 5 metros de B.
Sendo m medido em quilogramas e h em metros, o valor da
força de atrito F, suposta constante enquanto o corpo se
movimenta, vale, em newtons:
Considere: g = 10 m/s£
a) F = (1/2) mh
b) F = mh
c) F = 2 mh
d) F = 5 mh
e) F = 10 mh
26. (Ufes) Um objeto de massa igual a 2,0 kg, inicialmente em
repouso, percorre uma distância igual a 8,0 m em uma superfície
horizontal sem atrito, sob a ação de uma força constante,
também horizontal, igual a 4,0 N. A variação da energia cinética
do objeto é
a) 4,0 J
b) 8,0 J
c) 16,0 J
d) 32,0 J
e) 64,0 J
27. (Unesp) Conta-se que Newton teria descoberto a lei da
gravitação ao lhe cair uma maçã na cabeça. Suponha que
Newton tivesse 1,70 m de altura e se encontrasse em pé e que a
maçã, de massa 0,20 kg, tivesse se soltado, a partir do repouso,
de uma altura de 3,00 m do solo. Admitindo g = 10 m/s£ e
desprezando-se a resistência do ar, pode-se afirmar que a
energia cinética da maçã, ao atingir a cabeça de Newton, seria,
em joules, de
a) 0,60.
b) 2,00.
c) 2,60.
d) 6,00.
e) 9,40.
28. (Fuvest-gv) Uma empilhadeira elétrica transporta do chão
até uma prateleira, a 6 m do chão, um pacote de 120 kg. O
gráfico adiante ilustra a altura do pacote em função do tempo. A
potência aplicada ao corpo pela empilhadeira é:
a) 120 W
b) 360 W
c) 720 W
d) 1200 W
e) 2400 W
29. (Unesp) Um motor de potência útil igual a 125 W,
funcionando como elevador, eleva a 10 m de altura, com
velocidade constante, um corpo de peso igual a 50 N, no tempo
de
a) 0,4 s
b) 2,5 s
c) 12,5 s
d) 5,0 s
e) 4,0 s
30. (Unesp) O teste Margaria de corrida em escada é um meio
rápido de medida de potência anaeróbica de uma pessoa.
Consiste em fazê-la subir uma escada de dois em dois degraus,
cada um com 18 cm de altura, partindo com velocidade máxima
e constante de uma distância de alguns metros da escada.
Quando pisa no 8¡. degrau, a pessoa aciona um cronômetro,
que se desliga quando pisa no 12¡. degrau. Se o intervalo de
tempo registrado para uma pessoa de 70 kg foi de 2,8 s e
considerando a aceleração da gravidade igual a 10 m/s£, a
potência média avaliada por este método foi de
a) 180 W.
b) 220 W.
c) 432 W.
d) 500 W.
e) 644 W.
31. (Cesgranrio) Dois carrinhos A e B, de massas mÛ = 4,0 kg e
m½ = 2,0 kg, movem-se sobre um plano horizontal sem atrito,
com velocidade de 3,0 m/s. Os carrinhos são mantidos presos
um ao outro através de um fio que passa por dentro de uma
mola comprimida (fig.1). Em determinado momento, o fio se
rompe e a mola se distende, fazendo com que o carrinho A pare
(fig. 2), enquanto que o carrinho B passa a se mover com
velocidade V½. Considere que toda a energia potencial elástica
da mola tenha sido transferida para os carrinhos.
33. (G1) Duas pedras são lançadas do mesmo ponto no solo no
mesmo sentido. A primeira tem velocidade inicial de módulo 20
m/s e forma um ângulo de 60° com a horizontal, enquanto, para
a outra pedra, este ângulo é de 30°.
Considere que a primeira pedra tem 0,1 kg de massa. A energia
cinética no ponto mais alto da órbita e o trabalho realizado pelo
seu peso, entre o ponto de lançamento e o ponto em que atinge
o solo, são iguais, respectivamente, a:
a) 5,0 J e zero
b) 5,0 J e 20 J
c) 20 J e zero
d) 20 J e 5,0 J
e) zero e 20 J
34. (G1) Uma bola de pingue-pongue é abandonada de uma
altura h. Se 20% de sua energia se perde a cada batida no solo,
ela atingirá uma altura máxima menor que h/2, a partir do
choque de número
a) 2.
b) 3.
c) 4.
d) 5.
A velocidade que o carrinho B adquire, após o fio se romper,
vale, em m/s:
a) 6,0
b) 9,0
c) 12
d) 15
e) 18
35. (G1) Em um sistema conservativo, onde a energia mecânica
de 10 J se mantém constante e é composta da soma da energia
potencial e a energia cinética (EM = Ec + EP), fez-se um
experimento e foi obtido o gráfico a seguir, de energia potencial
× tempo. Com base no gráfico, assinale a alternativa CORRETA:
32. (Fuvest) No rótulo de uma lata de leite em pó lê-se:
"Valor energético: 1 509 kJ por 100 g (361 kcal)".
Se toda energia armazenada em uma lata contendo 400 g de
leite fosse utilizada para levantar um objeto de 10 kg, a altura
atingida seria de aproximadamente:
Dado: g = 10 m/s£
a) 25 cm.
b) 15 m.
c) 400 m.
d) 2 km.
e) 60 km.
a) A energia mecânica diminui entre 10 e 15 segundos.
b) A energia potencial é máxima em 10 segundos.
c) O corpo atinge a velocidade máxima em 5 segundos.
d) A velocidade do corpo aumenta entre 15 e 20 segundos.
e) A energia cinética diminui no intervalo de 0 até 5 segundos.
36. (Mackenzie) A figura mostra o instante em que uma esfera
de 4 kg é abandonada do repouso, da posição P, e cai sobre a
mola ideal de constante elástica 2.10£ N/m. O maior valor da
velocidade atingida por essa esfera, no seu movimento
descendente, é
38. (Unitau) Quando um objeto está em queda livre,
a) sua energia cinética se conserva.
b) sua energia potencial gravitacional se conserva.
c) não há mudança de sua energia total.
d) a energia cinética se transforma em energia potencial.
e) nenhum trabalho é realizado sobre o objeto.
39. (Uepg) A respeito de energia, assinale o que for correto.
(01) Energia potencial é aquela que se encontra armazenada
num determinado sistema e pode ser utilizada a qualquer
momento para realizar trabalho.
(02) No sistema conservativo, o decréscimo da energia potencial
é compensado por um acréscimo da energia cinética.
(04) A energia está relacionada com a capacidade de produzir
movimento.
(08) A energia pode ser transformada ou transferida, mas nunca
criada ou destruída.
a) 3 m/s
b) 4 m/s
c) 5 m/s
d) 6 m/s
e) 7 m/s
37. (Pucsp) O automóvel da figura tem massa de 1,2 . 10¤ kg e,
no ponto A, desenvolve uma velocidade de 10 m/s.
Estando com o motor desligado, descreve a trajetória mostrada,
atingindo uma altura máxima h, chegando ao ponto B com
velocidade nula. Considerando a aceleração da gravidade local
como g = 10 m/s£ e sabendo-se que, no trajeto AB, as forças
não conservativas realizam um trabalho de módulo 1,56 . 10¦ J,
concluímos que a altura h é de
a) 12 m
b) 14 m
c) 16 m
d) 18 m
e) 20 m
40. (Mackenzie) Durante sua apresentação numa "pista de
gelo", um patinador de 60 kg, devido à ação exclusiva da
gravidade, desliza por uma superfície plana, ligeiramente
inclinada em relação à horizontal, conforme ilustra a figura a
seguir. O atrito é praticamente desprezível. Quando esse
patinador se encontra no topo da pista, sua velocidade é zero e
ao atingir o ponto mais baixo da trajetória, sua quantidade de
movimento tem módulo
a) 1,20 . 10£ kg . m/s
b) 1,60 . 10£ kg . m/s
c) 2,40 . 10£ kg . m/s
d) 3,60 . 10£ kg . m/s
e) 4,80 . 10£ kg . m/s
Dados:
g = 10 m/s£
41. (Unesp) Um bloco de massa 0,10 kg desce ao longo da
superfície curva mostrada na figura adiante, e cai num ponto
situado a 0,60 m da borda da superfície, 0,40 s depois de
abandoná-la.
Desprezando-se a resistência oferecida pelo ar, pode-se afirmar
que o módulo (intensidade) da quantidade de movimento do
bloco, no instante em que abandona a superfície curva é, em
kg.m/s,
44. (Fuvest) Dois patinadores de mesma massa deslocam-se
numa mesma trajetória retilínea, com velocidades
respectivamente iguais a 1,5 m/s e 3,5 m/s. O patinador mais
rápido persegue o outro. Ao alcançá-lo, salta verticalmente e
agarra-se às suas costas, passando os dois a deslocar-se com
velocidade v. Desprezando o atrito, calcule o valor de v.
a) 1,5 m/s.
b) 2,0 m/s.
c) 2,5 m/s.
d) 3,5 m/s.
e) 5,0 m/s.
45. (Fuvest) Os gráficos a seguir representam as velocidades,
em função do tempo, de dois objetos esféricos homogêneos
idênticos, que colidem frontalmente. Se p é a quantidade de
movimento do sistema formado pelos dois objetos e E a energia
cinética deste mesmo sistema, podemos afirmar que na colisão:
a) p se conservou e E não se conservou.
b) p se conservou e E se conservou.
c) p não se conservou e E se conservou.
d) p não se conservou e E não se conservou.
e) (p + E) se conservou.
a) 0,10.
b) 0,15.
c) 0,20.
d) 0,25.
e) 0,30.
42. (Unesp) Uma nave espacial de 10¤ kg se movimenta, livre de
quaisquer forças, com velocidade constante de 1 m/s, em
relação a um referencial inercial. Necessitando pará-la, o centro
de controle decidiu acionar um dos motores auxiliares, que
fornecerá uma força constante de 200 N, na mesma direção,
mas em sentido contrário ao do movimento. Esse motor deverá
ser programado para funcionar durante:
a) 1 s.
b) 2 s.
c) 4 s.
d) 5 s.
e) 10 s.
43. (Unifesp) Uma menina deixa cair uma bolinha de massa de
modelar que se choca verticalmente com o chão e pára; a
bolinha tem massa 10 g e atinge o chão com velocidade de 3,0
m/s. Pode-se afirmar que o impulso exercido pelo chão sobre
essa bolinha é vertical, tem sentido para
a) cima e módulo 3,0 . 10-£ N . s.
b) baixo e módulo 3,0 . 10-£ N . s.
c) cima e módulo 6,0 . 10-£ N . s.
d) baixo e módulo 6,0 . 10-£ N . s.
e) cima e módulo igual a zero.
46. (Fuvest) Um corpo A com massa M e um corpo B com
massa 3M estão em repouso sobre um plano horizontal sem
atrito como mostra a figura a seguir. Entre eles existe uma mola,
de massa desprezível, que está comprimida por meio de um
barbante tensionado que mantém ligados os dois corpos. Num
dado instante, o barbante é cortado e a mola distende-se,
empurrando as duas massas, que dela se separam e passam a
se mover livremente. Designando-se por T a energia cinética,
pode-se afirmar que:
a) 9TÛ = T½
b) 3TÛ = T½
c) TÛ = T½
d) TÛ = 3T½
e) TÛ = 9T½
47. (Fuvest) Uma quantidade de barro de massa 2,0 kg é atirada
de uma altura h = 0,45 m, com uma velocidade horizontal v = 4
m/s, em direção a um carrinho parado, de massa igual a 6,0 kg,
como mostra a figura adiante. Se todo o barro ficar grudado no
carrinho no instante em que o atingir, o carrinho iniciará um
movimento com velocidade, em m/s, igual a
a) 3/4.
b) 1.
c) 5/4.
d) 2.
e) 3.
48. (Ita) Todo caçador, ao atirar com um rifle, mantém a arma
firmemente apertada contra o ombro evitando assim o "coice" da
mesma. Considere que a massa do atirador é 95,0 kg, a massa
do rifle é 5,00 kg e a massa do projétil é 15,0 g a qual é
disparada a uma velocidade de 3,00 × 10¥ cm/s. Nestas
condições, a velocidade de recuo do rifle (Vr) quando se segura
muito frouxamente a arma e a velocidade de recuo do atirador
(Va) quando ele mantém a arma firmemente apoiada no ombro
serão, respectivamente:
a) 0,90 m/s; 4,7 × 10-£ m/s
b) 90,0 m/s; 4,7 m/s
c) 90,0 m/s; 4,5 m/s
d) 0,90 m/s; 4,5 × 10-£ m/s
e) 0,10 m/s; 1,5 × 10-£ m/s
49. (Puc-rio) Um patinador de massa m‚ = 80 kg, em repouso,
atira uma bola de massa m• = 2,0 kg para frente com energia
cinética de 100 J. Imediatamente após o lançamento, qual a
velocidade do patinador em m/s?
(Despreze o atrito entre as rodas do patins e o solo)
a) 0,25
b) 0,50
c) 0,75
d) 1,00
e) 1,25
50. (Ufjf) Um avião bombardeiro, voando em linha reta com uma
velocidade V na horizontal, solta uma bomba que se fragmenta
em duas partes em algum instante antes de tocar o solo.
Sabendo-se que a massa total da bomba é M e que um dos
fragmentos fica com massa (1/3)M e a outra (2/3)M, se os
fragmentos tocam o solo simultaneamente, qual a razão entre as
distâncias horizontais do fragmento menor e do fragmento
maior, quando as mesmas tocam o solo, em relação à posição
do avião na direção horizontal? Despreze a resistência do ar e
considere que a topografia do local seja totalmente plana.
a) 1/6.
b) 1/2.
c) 2.
d) 3.
e) 6.
51. (Fuvest) Perto de uma esquina, um pipoqueiro, P, e um
"dogueiro", D, empurram distraidamente seus carrinhos, com a
mesma velocidade (em módulo), sendo que o carrinho do
"dogueiro" tem o triplo da massa do carrinho do pipoqueiro. Na
esquina, eles colidem (em O) e os carrinhos se engancham, em
um choque totalmente inelástico.
Uma trajetória possível dos dois carrinhos, após a colisão, é
compatível com a indicada por
a) A
b) B
c) C
d) D
e) E
52. (G1) Considere a colisão entre dois automóveis. No instante
exato da colisão, é(são) conservada(s) a(s) seguinte(s)
grandeza(s) física(s):
a) apenas a energia mecânica
b) apenas o momento linear
c) a energia mecânica e o momento linear
d) a energia e o momento linear
e) a energia e a energia mecânica
53. (Uece) Por transportar uma carga extremamente pesada, um
certo caminhão trafega a uma velocidade de 10 m/s. Um rapaz à
beira da estrada brinca com uma bola de tênis. Quando o
caminhão passa, ele resolve jogar a bola na traseira do mesmo.
Sabendo-se que a bola atinge a traseira do caminhão
perpendicularmente, com velocidade de 20 m/s, em relação ao
solo, qual a velocidade horizontal final da bola após o choque ?
Considere um choque perfeitamente elástico.
a) 10 m/s
b) 20 m/s
c) 30 m/s
d) Zero
54. (Ufpe) Uma bala de massa m = 20 g e velocidade v = 500
m/s atinge um bloco de de massa M = 480 g e velocidade V = 10
m/s, que se move em sentido contrário sobre uma superfície
horizontal sem atrito. A bala fica alojada no bloco. Calcule o
módulo da velocidade do conjunto (bloco + bala), em m/s, após
colisão.
a) 10,4
b) 14,1
c) 18,3
d) 22,0
e) 26,5
55. (Ufrs) Uma pistola dispara um projétil contra um saco de
areia que se encontra em repouso, suspenso a uma estrutura
que o deixa plenamente livre para se mover. O projétil fica
alojado na areia. Logo após o impacto, o sistema formado pelo
saco de areia e o projétil move-se na mesma direção do disparo
com velocidade de módulo igual a 0,25 m/s. Sabe-se que a
relação entre as massas do projétil e do saco de areia é de
1/999.
Qual é o módulo da velocidade com que o projétil atingiu o alvo?
a) 25 m/s.
b) 100 m/s.
c) 250 m/s.
d) 999 m/s.
e) 1000 m/s.
56. (Ufu) Uma pequena esfera de massa M•, inicialmente em
repouso, é abandonada de uma altura de 1,8 m de altura,
posição A da figura a seguir. Essa esfera desliza sem atrito
sobre um trilho, até sofrer um choque inelástico com outra esfera
menor, inicialmente parada, de massa M‚. O deslocamento das
esferas ocorre sem rolamentos. Após o choque, as duas esferas
deslocam-se juntas e esse deslocamento ocorre sem atrito.
A aceleração da gravidade no local é de 10 m/s£. Sendo a
massa M duas vezes maior que M‚, a altura em relação à base
(linha tracejada) que as duas esferas irão atingir será de
a) 0,9 m.
b) 3,6 m.
c) 0,8 m.
d) 1,2 m.
57. (Unesp) Um corpo A de massa m, movendo-se com
velocidade constante, colide frontalmente com um corpo B, de
massa M, inicialmente em repouso. Após a colisão,
unidimensional e inelástica, o corpo A permanece em repouso e
B adquire uma velocidade desconhecida. Pode-se afirmar que a
razão entre a energia cinética final de B e a inicial de A é:
a) M£/m£
b) 2m/M
c) m/2M
d) M/m
e) m/M
58. (Unesp) Um bloco A, deslocando-se com velocidade v³ em
movimento retilíneo uniforme, colide frontalmente com um bloco
B, inicialmente em repouso. Imediatamente após a colisão,
ambos passam a se locomover unidos, na mesma direção em
que se locomovia o bloco A antes da colisão. Baseado nestas
informações e considerando que os blocos possuem massas
iguais, é correto afirmar que
a) a velocidade dos blocos após a colisão é v³/2 e houve
conservação de quantidade de movimento e de energia.
b) a velocidade dos blocos após a colisão é v³ e houve
conservação de quantidade de movimento e de energia.
c) a velocidade dos blocos após a colisão é v³ e houve apenas
conservação de energia.
d) a velocidade dos blocos após a colisão é v³/2 e houve apenas
conservação de quantidade de movimento.
e) a velocidade dos blocos após a colisão é v³/2 e houve apenas
conservação de energia.
59. (Mackenzie) Ao nível do mar, certa pessoa necessitou
aquecer 2,0 litros d'agua, utilizando um aquecedor elétrico de
imersão, cuja potência útil e constante é igual a 1,0 kW. O
termômetro disponibilizado estava calibrado na escala
Fahrenheit e, no início do aquecimento, a temperatura indicada
era 122 °F. O tempo mínimo necessário para que a água
atingisse a temperatura de ebulição foi
a) 1 min 40 s
b) 2 min
c) 4 min 20 s
d) 7 min
e) 10 min
Dados:
›água = 1,0 g/cm¤
cágua = 1,0cal/(g . °C)
1 cal = 4,2 J
60. (Pucsp) A experiência de James P. Joule, determinou que é
necessário transformar aproximadamente 4,2 J de energia
mecânica para se obter 1 cal. Numa experiência similar,
deixava-se cair um corpo de massa 50 kg, 30 vezes de uma
certa altura. O corpo estava preso a uma corda, de tal maneira
que, durante a sua queda, um sistema de pás era acionado,
entrando em rotação e agitando 500 g de água contida num
recipiente isolado termicamente. O corpo caia com velocidade
praticamente constante. Constatava-se, através de um
termômetro adaptado ao aparelho, uma elevação total na
temperatura da água de 14 °C.
Determine a energia potencial total perdida pelo corpo e de que
altura estava caindo.
Despreze os atritos nas polias, no eixo e no ar.
Dados: calor específico da água: c = 1 cal/g °C g = 9,8 m/s£.
a) Ep = 7000 J; h = 0,5 m.
b) Ep = 29400 J; h = 2 m.
c) Ep = 14700 J; h = 5 m.
d) Ep = 7000 J; h = 14 m.
e) Ep = 29400 J; h = 60 m.
GABARITO
b) 2,0 m/s.
1. a = 2m/s£
20 J e 30 J
16. a) 4,0 m/s.
b) 2,0 . 10£ J.
2. a) 200 J.
b) 8,0 N.
17. a) o corpo de massa m inverterá o sentido de seu movimento
com velocidade de módulo igual a Ë(2gh)/3 e o corpo de massa
2m iniciará seu movimento com 2.Ë(2gh)/3
3. a) 45 J.
b) 10 J.
b) ÐE = -(4/9).mgh
4. a) (™/20) rad/s.
b) 5,0 m/s£.
c) 4000 N.
d) 2,0.10¦ W.
18. a) 480 J.
b) 2/3.
5. a) 200 J e 150 J.
b) 20 W e 75 W.
20. [E]
19. [C]
21. [E]
6. a) 6,75 .10¦ J.
b) 90 CV.
7. a) 40 N.
b) 2,0 m/s.
22. [A]
23. [D]
24. [A]
8. a) 1800 J
b) Pa = Pb = Pc
25. [C]
9. Pela conservação da energia mecânica:
Eg(A) + Ec(A) = Eg(B)
m.g.h(A) + mv£/2 = m.g.h(B)
Simplificando por m:
g.h(A) + v£/2 = g.h(B)
10.8 + v£/2 = 10.13
80 + v£/2 = 130
v£/2 = 130 - 80
v£/2 = 50
v£ = 50.2 = 100
v = 10 m/s
26. [D]
10. V(depois da colisão) = 2,0 m/s
32. [E]
11. 50 J.
33. [A]
12. 3,8 . 10¤ N
34. [C]
13. A velocidade (V) do tubo após a saída da rolha, pelo
princípio da conservação da energia é:
Energia do tubo = Energia do tubo suspenso ë (M.V£)/2 =
M.g.L ë V = Ë(2.g.L).
35. [C]
14. a) 3,0 m/s.
b) 3,0 . 10£ m/s.
15. a) 1,2 J.
27. [C]
28. [B]
29. [E]
30. [A]
31. [B]
36. [B]
37. [A]
Pela conservação:
m.v£/2 + mgh = mgh' + •(não conservativo)
1200.10£/2 + 1200.10.20 = 1200.10.h' + 1,56.10¦
60000 + 240000 = 12000.h' + 156000
30000 - 156000 = 12000h'
144000 = 12000.h'
144000/12000 = h' ==> h' = 12 m
38. [C]
39. 1 + 2 + 4 + 8 = 15
40. [C]
41. [B]
42. [D]
43. [A]
44. [C]
45. [A]
46. [D]
47. [B]
48. [D]
49. [A]
50. [C]
51. [B]
52. [D]
53. [D]
54. [A]
55. [C]
56. [C]
57. [E]
58. [D]
59. [D]
60. [B]