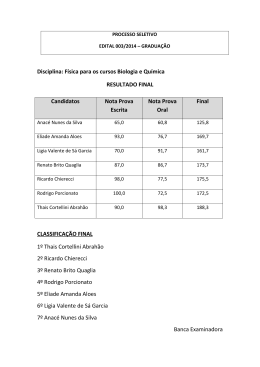
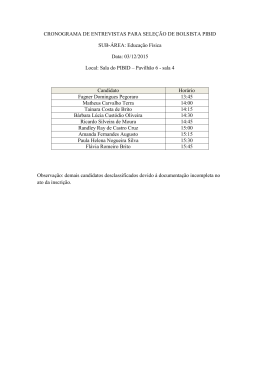
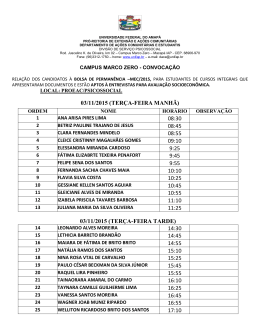
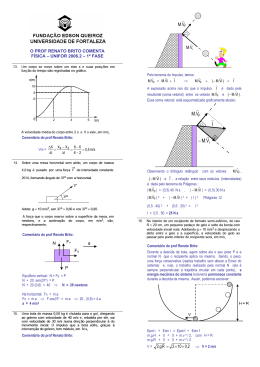
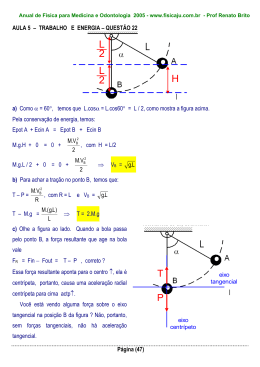
PROVA DA UFC 2009.1 – COMENTADA
Prof. Renato Brito
O prof Renato Brito Comenta:
R1 = 1 x 10−6 m,
Q1 = 10.000.e
R2 = 1 x 10−3 m
Q2 = 10n.e
σ1 = σ2 ⇒
Q1
4π.(R1 )2
=
Q2
4π.(R2 )2
⇒
10 4.e
(10−6 )2
=
10n.e
(10−3 )2
⇒
n = 10
Assim, a ordem de grandeza pedida vale 10n = 1010
Resposta : D
O prof Renato Brito Comenta:
Essa questão tem um enunciado absolutamente claro e preciso. Para não deixar margem a interpretações
alternativas, foram acrescentados ao desenho dois símbolos de ângulo reto (90 graus), para assegurar que, no
momento em que o fio se rompe, ele encontra-se horizontal, e a velocidade do projétil encontra-se na direção
vertical apontando para cima V↑.
Após o fio se romper, a bola prossegue V↑ em seu movimento de subida vertical sob ação exclusiva da força peso
P↓ que age na mesma direção da velocidade (direção tangencial). A bola não sofre ação de nenhuma força na
direção centrípeta (direção perpendicular à velocidade), portanto, o corpo se move livre da ação de forças
centrípetas, o que garante que sua trajetória NÃO PODERÁ SER CURVILÍNEA, ou seja, só poderá ser
RETILÍNEA.
Assim, a bola sobe e desce em trajetória retilínea, como indicado na letra A.
Resposta : A
O prof Renato Brito Comenta:
Acredito que a maioria dos estudantes deva conhecer a famosa fórmula abaixo, para a determinação do menor
ângulo formado entre os ponteiros de um relógio :
α=
| 60.H − 11.M |
, com H = 0, 1, 2, 3, ..., 10, 11 e M = 0, 1, 2, 3, ....., 59
2
Assim, a questão pede que determinemos em quanto tempo, após as 3h, o ângulo α formado entre os ponteiros
do relógio valerá zero:
| 60.H − 11.M | | 60 × 3 − 11.M |
180 176 + 4
4
=
= 0 ⇒ 11.M = 180 ⇒ M =
=
=16+
, ou seja:
2
2
11
11
11
4
4
240
231 + 9
231 + 9
16min +
min = 16min +
(60s) = 16min +
s = 16min +
s = 16min +
s=
11
11
11
11
11
9
81
= 16min + 21 s = 16min + 21 s
11
99
α=
Lamentavelmente, a CCV de Física colocou uma questão de Matemática na prova de Física. Certamente, teria
sido mais rico e abrangente, se essa questão de Matemática tivesse dado lugar a uma questão de
Gases/Termodinâmica, Hidrostática ou de Óptica.
Resposta : D
O prof Renato Brito Comenta:
Pelo Principio do Trabalho Total (Teorema da Energia cinética) no percurso PQR, podemos escrever:
Τtotal = ΤPeso + ΤNormal
ΤFat = Ecin F − Ecin i
+
Sendo P a posição inicial e R a posição final, supondo que o trecho PQR seja horizontal, podemos escrever :
Τtotal = ΤPeso + ΤNormal +
Τtotal = 0 + 0
+
ΤFat = Ecin F − Ecin i
( −Fat1.L1 −
−μ.m.g.L1 − 2μ.m.g.L2 = −
=
m.v 2
2
0 −
m.v 2
, com L2 = L − L1
2
μ.m.g.L1 + 2μ.m.g.( L − L1 ) =
2μ.m.g.L − μ.m.g.L1 =
Fat2.L2 )
m.v 2
2
Sendo L2 = L − L1, vem: L2 =
m.v 2
2
⇒
μ.m.g.L1 = 2μ.m.g.L −
m.v 2
2
⇒
L1 = 2L −
v2
2.μ.g
v2
− L
2.μ.g
Assim, quando o problema é resolvido usando Trabalho e Energia, a sua solução é relativamente simples. Em
geral, questões literais tendem a amedrontar facilmente os estudantes já traumatizados com a Física. Com isso,
alguns estudantes podem considerar difícil essa questão.
Resposta : A
O prof Renato Brito Comenta:
Trata-se de uma questão bem conhecida, comum a todos os livros de Calorimetria de Ensino Médio. Essa talvez
seja a questão mais fácil da prova. Essa era para nenhum candidato zerar a prova. Pela conservação da energia,
podemos escrever:
QA + QB + QC = 0
mA.c.(TF − Ti) + mB.c.(TF − Ti) + mC.c.(TF − Ti)
m. c. (TF − T) +
16.(TF − T) +
=
m ⎛
T⎞
m ⎛
T⎞
.c. ⎜ TF − ⎟ +
.c. ⎜ TF − ⎟ = 0
2 ⎝
2⎠
4 ⎝
4⎠
( 8TF − 4T )
+
( 4TF − T )
= 0
⇒
0
multiplicando, membro a membro, por 16, vem:
28.TF = 21T
⇒
TF = 3T/4
Resposta : B
O prof Renato Brito Comenta:
A intensidade de uma onda a uma distância D da fonte é dada por:
I=
Pot emitida
x
4πD2
Pot1
4π.x
2
=
Pot1
4π.x
Pot 2
4π.y
2
2
=
⇒
Pot 2
4π.y 2
, com Pot1 = 4.Pot2.
4.Pot 2
4π.x
P2
y
L
Assim, do enunciado do questão, temos:
I1 = I2 ⇒
Q
P1
2
=
Pot 2
4π.y 2
Resolvendo o sistema, encontramos:
⇒
x = 2.y , com x + y = L.
x = 2L/3
Resposta : C
Você não entendeu nem sequer o enunciado da questão 59 ? ☺ Nem eu. Fique
tranqüilo, o enunciado não está nem um pouco claro. Escrevi um enunciado mais claro
para essa questão a seguir :
59) O circuito principal da figura encontra-se fixo a uma mesa horizontal sem atrito. Uma barra de comprimento
L = 30 cm e resistência desprezível está conectada a um par de molas inicialmente relaxadas (de constantes
elásticas K = 2 N/m e resistência R = 0,05Ω cada uma) e pode se mover ao longo da mesa, devido a ação
de um campo magnético uniforme de intensidade B = 0,01T, perpendicular ao plano da pagina e entrando na
mesma.
O circuito em anexo também está sobre a mesa, fixo próximo ao circuito principal, porém encontra-se aberto
em sua extremidade superior, e para fechá-lo, conta-se com a ajuda de uma extremidade condutora que
deverá se deslocar uma distancia d = 3 cm (veja a figura) até fazer contato com a extremidade aberta do
circuito anexo, fechando o mesmo.
Determine o valor da força eletromotriz ε (no circuito principal) que proporcionará esse deslocamento da barra
necessário para fechar o circuito em anexo.
O prof Renato Brito Comenta:
A barra será percorrida por uma corrente elétrica i ← sob ação de um campo magnético B 8 que, pela regra da
mão direita, exercerá sobre essa barra uma força magnética ↓ de intensidade FM = B.i.L.sen90o. Tal força
magnética deverá mover a barra no sentido de comprimir o par de molas até produzir nas mesmas a deformação
x = d = 3 cm. Assim, a barra se deslocará d = 3 cm e sua extremidade condutora fará contato com o circuito
anexo, fechando o mesmo.
Admitindo o equilíbrio da barra em sua posição final, podemos escrever o
equilíbrio das forças de acordo com o diagrama ao lado:
Fmag = Fel + Fel
⇒
B.i.L = k.x + k.x
⇒
i=
⇒
Fel
2k.x 2.2.(3.10 )
=
= 40A
B.L
0,01× 0,3
Agora, determinemos a fem que produz essa corrente na barra:
ε = (R + R) . i ⇒ ε = (0,05 + 0,05) . 40
Fel
−2
Fmag
ε = 4V
Resposta : E
O prof Renato Brito Comenta:
Sabemos que a velocidade da luz (luz, laser, qualquer onda eletromagnética, fótons, grávitons), no vácuo, é
sempre a mesma, em qualquer referencial inercial, valendo sempre c. Desse fato, já excluímos as alternativas D
e E.
Sabemos também que a velocidade v de qualquer corpo que possua massa de repouso é sempre menor que a
velocidade da luz no vácuo, isto é, v < c. Desse fato, já excluímos as alternativas A e C !!!! ☺
A única alternativa que satisfaz essas condições acima é dada pela letra B. Assim, mesmo que o estudante não
conhecesse a pouco divulgada fórmula da velocidade relativa relativística, ainda assim, com paciência e jogo de
cintura, teria facilmente acertado essa questão 60 da prova.
Resposta : B
Comentário Geral sobre essa prova:
Considerando o tempo de prova e o nervosismo usual dos vestibulandos, essa prova pode levar muitos alunos a
uma nota indesejada.
Tirando o enunciado CONFUSO da questão de magnetismo, um aluno que tivesse auto-controle, tivesse
equilíbrio para vencer a pressão do tic-tac do relógio, tendo muita fibra para vencer o problema do tempo, poderia
obter até mesmo uma nota de média a alta nessa prova.
Acredito que estava mais ASSUSTADORA do que propriamente difícil, a princípio.
Na minha opinião, estava no mesmo grau de dificuldade da prova do final do ano passado.
Lamentei a ausência de questões de Óptica e Termodinâmica, que devem ter sido guardadas para a 2ª fase do
vestibular.
Prof. Renato Brito