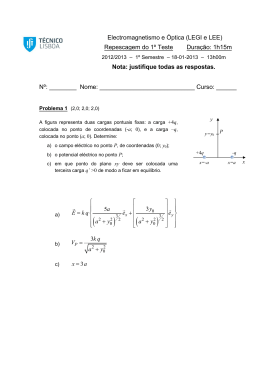
22.31
21.41
Duas cargas puntiformes q são colocadas sobre o eixo Ox, uma no ponto x = a e outra no ponto x = -a. a)
Determine o módulo, a direcção e o sentido do campo eléctrico no ponto x = 0. b) Deduza uma expressão para o campo
eléctrico em qualquer ponto sobre o eixo Ox. Use seu resultado para fazer um gráfico do campo eléctrico em função de x
para valores de x compreendidos entre -4a e +4a.
22.36
21.48
Um fio rectilíneo muito longo possui carga por unidade de comprimento igual a 1,50 x 10-'° C/m. A que distância
do fio o módulo do campo eléctrico é igual a 2,50 N/C?
22.38
21.50
Um condutor em forma de anel com raio a = 2,50 cm possui uma carga positiva Q = +0,125 nC uniformemente
distribuída ao longo do anel, como indica a Figura 22.17. O centro do anel está na origem O do sistema de coordenadas,
a) Qual é o campo eléctrico (módulo, direcção e sentido) no ponto P situado em x = 40,0 cm? b) Uma carga puntiforme
q - -2,50 //C está no ponto P descrito na parte (a). Determine o módulo, a direcção e o sentido da força exercida pela
carga q sobre o anel.
22.45
21.57
a) Faça um esboço das linhas de campo eléctrico para um fio rectilíneo infinito uniformemente carregado. Você poderá
achar útil fazer o desenho das linhas de campo num plano que contém o fio carregado separadamente do desenho das linhas de
campo num plano ortogonal ao fio. b) Explique como seus desenhos mostram que i) o módulo E do campo eléctrico depende
somente da distância r entre o ponto e o fio ii) E diminui com l/r
22.48
21.60
A molécula de cloreto de potássio (KCl) possui um momento de dipólo eléctrico igual a 8,9 x IO-30 C • m. a)
Supondo que esse momento de dipólo eléctrico seja produzido por duas cargas ±1,6 x 10-19 C separadas por uma distância
d, determine d. b) Qual é o valor máximo do módulo do torque que um campo eléctrico uniforme com módulo igual a 6,0 x
105 N/C pode exercer sobre a molécula de KCl? Faça um desenho para mostrar a orientação relativa entre o vectorr
momento dipolar eléctrico p e o campo eléctrico E quando o torque atinge seu valor máximo.
PROBLEMAS
22.54
21.70
Duas esferas idênticas de massa m estão suspensas em fios de seda de comprimento L, como indicado na Figura.
Cada esfera possui a mesma carga; logo, q1 = q2 = q. O raio de cada esfera é muito pequeno em comparação com a distância
entre as esferas, de modo que elas podem ser consideradas cargas puntiformes. Mostre que, se o ângulo θ for pequeno, a
distância d no equilíbrio entre as esferas será dada por d = (q2L/2πε0mg)1/3 (Dica: Quando θ for pequeno, então tan θ ≈ sen θ)