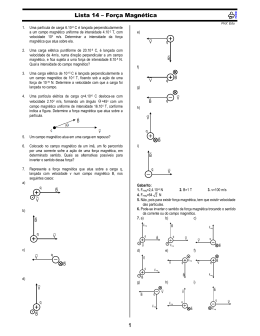
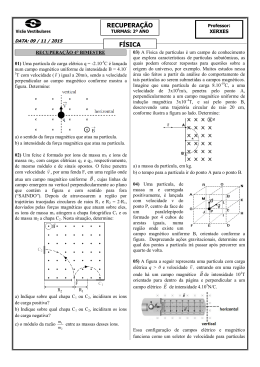
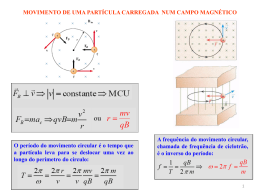
Simulado – UFPR 2ª fase – Física 3
Prof. Paulo Roberto Fiatte Carvalho
Orientações:





Esse simulado foi elaborado com a intenção de auxiliar em seu estudo
para a prova discursiva de 2ª fase – UFPR -2015.
Para resolvê-lo utilize somente o formulário disponibilizado pela UFPR.
No final do simulado encontra-se a resolução de cada questão, procure
olhar somente após resolvê-las.
Qualquer duvida estou a disposição.
Estou torcendo pelo seu sucesso e tenho certeza que juntos
chegaremos à conquista de sua vaga. Conte comigo.
1. (Ufpr 2014) Um próton é injetado no ponto O e passa a se mover no interior de um
capacitor plano de placas paralelas, cujas dimensões estão indicadas na figura abaixo.
O próton tem velocidade inicial v 0 com módulo 1,0  105 m / s e direção formando um
ângulo θ igual a 45° com o eixo x horizontal. O campo elétrico está orientado na
direção do eixo y conforme mostrado na figura. Considere a massa do próton igual a
1,6  1027 kg e sua carga igual 1,6  1019 C. Supondo que somente o campo elétrico
uniforme no interior do capacitor atue sobre o próton, calcule qual deve ser o mínimo
módulo deste campo para que o próton não colida com a placa inferior.
2. (Ufpr 2014) Nas residências, é comum utilizarmos um aparelho chamado
“mergulhão”, “ebulidor” ou “rabo quente”, constituído essencialmente por um resistor
que, ao ser ligado a uma diferença de potencial, dissipa calor e aquece líquidos nos
quais está mergulhado. Suponha que a resistência do aparelho seja constante e igual
a 10 Ω, e que ele seja mergulhado num recipiente com um litro de água pura,
inicialmente a 20 °C. Considere que a densidade da água é 1000 kg/m3, seu calor
específico é 4187J / kg  C  e que o aparelho seja ligado a uma diferença de potencial
de 100 V. Despreze a capacidade térmica do aparelho e do recipiente. Com base
nestes dados, calcule quanto tempo leva para a água ser aquecida até a temperatura
de 60 °C, expressando seu resultado em segundos e utilizando apenas três
algarismos significativos.
3. (Ufpr 2014) Normalmente as pessoas estão acostumadas a comprar lâmpadas
considerando apenas a sua potência, em watts, pensando que quanto maior a
potência, maior será a iluminação. Contudo, a potência diz apenas qual é o consumo
de energia por unidade de tempo. Para ter uma ideia de qual lâmpada é capaz de
iluminar melhor o ambiente, deve-se utilizar o conceito de fluxo luminoso, que é
medido em lúmens (lm). Quanto mais lúmens, mais iluminado será o ambiente. Outro
conceito importante é a eficiência de uma lâmpada, que é dada pela razão entre o
fluxo luminoso e a sua potência, e permite avaliar o consumo de energia necessário
para produzir determinada iluminação. A tabela a seguir compara características de
diferentes lâmpadas residenciais. A vida útil é o tempo médio, em horas, que uma
lâmpada funciona antes de “queimar”.
Tipo
lâmpada
de
Incandescente
Fluorescente
LED
Potência (W)
Fluxo
luminoso (lm)
Vida útil (h)
60
15
8
800
800
800
14.000
10.000
50.000
Preço unitário
da
lâmpada
(R$)
1,50
10,00
50,00
Com bases nestas informações, responda os seguintes itens:
a) Se quisermos substituir 8 lâmpadas fluorescentes por lâmpadas de LED, mantendo
a mesma iluminação, calcule a diferença no consumo de energia durante um
período de 20.000 horas de funcionamento. Expresse o resultado em joules.
b) Calcule a diferença no custo da energia consumida, em R$, ao se utilizar uma
lâmpada fluorescente e uma lâmpada de LED após 20.000 horas de funcionamento.
Considere que o custo de 1 kWh de energia elétrica é igual a R$ 0,40. Inclua
também nesse cálculo o custo de substituição das lâmpadas, tendo como base a
vida útil das lâmpadas.
c) Com base nos dados da tabela acima, calcule quantas vezes uma lâmpada de LED
é mais eficiente que uma lâmpada incandescente.
4. (Ufpr 2014) Uma partícula de massa m e carga q, inicialmente se deslocando com
velocidade v, penetra numa região onde há um campo magnético uniforme de módulo
B e direção perpendicular à velocidade v. Na presença desse campo magnético, a
trajetória da partícula é uma circunferência. Com base nessas informações e nos
conceitos de eletricidade e magnetismo, deduza equações literais envolvendo as
variáveis dadas, para:
a) o raio da circunferência descrita pela partícula.
b) o tempo que a partícula leva para percorrer metade da distância desta trajetória
circular.
5. (Ufpr 2013) Considerando que todos os capacitores da associação mostrada na
figura abaixo têm uma capacitância igual a C, determine a capacitância do capacitor
equivalente entre os terminais A e B. Apresente a resolução.
6. (Ufpr 2013) Em 1820, Hans Cristian Oersted aproximou de uma bússola um fio
condutor percorrido por uma corrente elétrica e não observou qualquer alteração na
direção da agulha dessa bússola. Mais tarde, ao refazer o experimento, porém agora
com o fio condutor posicionado em outra direção, ele constatou que ocorria uma
alteração na direção da agulha da bússola. Essa experiência histórica fez a conexão
entre a eletricidade e o magnetismo, criando o que nós conhecemos hoje por
eletromagnetismo. Suponha uma bússola posicionada sobre esta folha de papel com
sua agulha apontando para a parte superior da folha, o que corresponde à direção
norte.
Utilizando a figura a seguir, desenhe a direção em que deverá ser posicionado o fio
condutor, passando exatamente sobre o centro da bússola, para que se obtenha o
maior desvio possível da sua agulha. Escolha um sentido para a corrente no fio,
marcando-o com uma seta na figura. Indique na figura para qual lado ocorrerá esse
desvio, se para leste ou para oeste, de modo compatível com o sentido da corrente
escolhido. Justifique suas respostas.
7. (Ufpr 2013) A investigação científica na área de física de partículas elementares
ganhou recentemente um poderoso aliado, o Grande Colisor de Hádrons. Nesse
laboratório serão realizadas diversas experiências com o objetivo de verificar a
existência de novas partículas elementares, além de determinar com maior precisão
propriedades físicas importantes de partículas já conhecidas. Uma experiência
relativamente simples feita nesse laboratório consiste em utilizar um equipamento
chamado de câmara de neblina. Nessa câmara há um vapor supersaturado, e quando
partículas passam por ele ocorre a condensação do vapor de água na forma de
bolhas, que mostram então as trajetórias descritas pelas partículas. Aplicando-se um
campo magnético B no local, é possível determinar grandezas relevantes, como carga
ou massa das partículas. Uma dessas experiências é ilustrada na figura abaixo. Uma
partícula de carga elétrica Q desconhecida entra numa câmara de neblina com uma
velocidade inicial v horizontal e no plano da página. O campo magnético B é
uniforme, perpendicular ao plano da página e está entrando nesta. Essa partícula fica
sujeita ao campo B e move-se em MRU até um certo instante em que ela sofre um
decaimento radioativo, transformando-se em duas partículas, de massas ma e mb,
cargas Qa e Qb, que descrevem as trajetórias circulares de raios Ra e Rb mostradas na
figura. As duas partículas iniciam o movimento circular com a mesma velocidade v da
partícula original e esse decaimento segue a lei de conservação das cargas.
a) Determine o sinal da carga Q da partícula que entrou no campo magnético,
justificando a resposta.
b) Determine os sinais das cargas das partículas que descrevem as trajetórias
circulares de raios Ra e Rb, e a relação entre as cargas Qa e Qb, justificando as
respostas.
8. (Ufpr 2011) A figura mostra um circuito formado por uma fonte de força eletromotriz
e cinco resistores. São dados: ε = 36 V, R1 = 2  , R2 = 4  , R3 = 2  , R4 = 4  e R5 =
2.
Com base nessas informações determine:
a) A corrente elétrica que passa em cada um dos resistores.
b) A resistência equivalente do circuito formado pelos resistores R1 a R5.
9. (Ufpr 2011) Uma das maneiras de gerar correntes elétricas é transformar energia
mecânica em energia elétrica através de um gerador elétrico. Em uma situação
simplificada, dispõe-se de ímãs para produzir o campo magnético e de uma bobina
formada por 10 espiras circulares com 10 cm de diâmetro montados conforme a figura
a seguir. A bobina está presa a um eixo que passa pelo seu diâmetro e gira com
velocidade constante de 2 rotações por segundo. A bobina possui dois terminais que
permitem o aproveitamento da energia elétrica gerada. Num dado instante, as linhas
do campo magnético atravessam perpendicularmente o plano das espiras e o fluxo
magnético é máximo; após a bobina girar 90° em torno do eixo, esse fluxo é zero.
Considere que na região da bobina o campo magnético é uniforme, com módulo igual
a 0,01 T e orientado conforme indicado na figura. Determine a força eletromotriz média
induzida na bobina ao girar 90° a partir da situação de máximo fluxo.
10. (Ufpr 2011) Uma experiência interessante, que permite determinar a velocidade v
com em que partículas elementares se movem, consiste em utilizar um campo
magnético B em combinação com um campo elétrico E . Uma partícula elementar com
carga Q negativa move-se com velocidade v paralelamente ao plano do papel
(referencial inercial) e entra em uma região onde há um campo magnético B uniforme,
constante e orientado para dentro do plano do papel, como mostra a figura. Ao se
deslocar na região do campo magnético, a partícula fica sujeita a uma força magnética
FM .
a) Obtenha uma expressão literal para o módulo de FM e represente na figura o vetor
FM para a posição indicada da partícula.
b) Dispõe-se de um sistema que pode gerar um campo elétrico E uniforme, constante
e paralelo ao plano do papel, que produz uma força elétrica FE sobre a partícula.
Represente na figura o vetor E necessário para que a partícula de carga Q mova-se
em movimento retilíneo uniforme. Em seguida, obtenha uma expressão literal para o
módulo da velocidade v da partícula quando ela executa esse movimento, em
função das grandezas apresentadas no enunciado.
Gabarito:
Resposta da questão 1:
Dados:
v0  1,0  105 m / s; m  1,6  1027 kg; q  1,6  1019 C; x  2 cm  2  102 m  y  10 cm  101m.
Decompondo a velocidade inicial:

5
v ox  v 0 cos 45  10



v oy  v 0 sen 45  105


2
 v 0x  5 2  104 m/s.
2
2
 v 0y  5 2  104 m/s.
2
A força resultante é a força elétrica, que tem o mesmo sentido do campo elétrico, pois o próton tem carga
positiva. Assim, o movimento da partícula é uniforme no eixo x e uniformemente retardado no eixo y.
No eixo x:
x  vx t  t 
x
101
2

 0,2
 105  t  2  106 s.
v x 5  2  104
2
No eixo y:

qE
.
R  Fel  m a  q E  a 
m

y  v t  1 a t2.
oy

2

2 m v 0y t  y
q E t2
 v 0y t  y  E 
2m
q t2
E

 y  v 0y t 


2  1,6  1027 5  2  10 4  2  10 6  2  10 2
1,6  1019 

2  10 6

2
1 qE 2
t 
2 m
  3,2  1027 8  102 
3,2  1031
E  8  102 N/C.
Resposta da questão 2:
Dados: R  10Ω; U  100V; V  1L  m  1kg; c  4.187J / kg  C; Δθ  40C.
U2
Δt  m c Δθ 
R
10  1 4187  40
Q  m c Δθ  P Δ t  m c Δθ
Δt 
R m c Δθ
U2
 Δt 

1002
Δt  167 s.
Resposta da questão 3:
a) Supondo que as lâmpadas fluorescentes a serem substituídas sejam de 15 W e que as de LED
sejam de 8 W, de acordo com a tabela, a quantidade de lâmpadas (n) será a mesma. Calculando a
diferença (Dif) pedida:
ΔEF  n PF Δ t

ΔEL  n PL Δ t
 Dif  ΔEF  ΔEL  PF  PL  n Δt 
Dif  15  8   8  20.000  3.600 
Dif  4  109 J.
b) A diferença no consumo de energia é:
Dif  15  8   20.000  140.000 Wh  140 kWh.
Como deverá haver uma troca da lâmpada fluorescente, haverá um gasto a mais de R$10,00, além do
consumo de energia. Então a diferença (C) no custo é:
C  140  0,40  10,00 
C  R$ 66,00.
c) Comparando as eficiências:
800

η 
Fluxo  L
8
η

800
Potência 
η 
 I
60

ηL 60


ηI
8
ηL  7,5 ηI .
Resposta da questão 4:
a) De acordo com o enunciado, o movimento é circular uniforme. Logo a força magnética sobre a
partícula age como resultante centrípeta.
Assim:
Fmag  Rcent 
q vB 
m v2
R

R
mv
.
qB
b) Teremos:
v
ΔS
ΔS π R
πm v 
 Δt 

 Δt  
 
Δt
v
v
v  q B 
Δt 
πm
.
qB
Resposta da questão 5:
A figura mostra uma sequência de simplificações do circuito, dando as capacitâncias equivalentes
parciais.
A capacitância equivalente é:
Ceq  2 C.
Resposta da questão 6:
Se o fio deve passar “exatamente” sobre o centro da bússola, ele deve furá-la nesse centro. Para que o
desvio seja máximo, o fio deve ser perpendicular à superfície sobre a qual a bússola está apoiada. Há
duas possibilidades: a corrente está entrando (fig. 1) ou saindo (fig. 2). Pela regra da mão direita
determinamos o sentido das linhas de indução magnética. O desvio da agulha é no sentido dessas linhas.
- Na fig. 1, a corrente está entrando. O sentido das linhas de indução magnética é horário, desviando a
extremidade imantada da agulha no sentido leste.
- Na fig. 2, a corrente está saindo. O sentido das linhas de indução magnética é anti-horário, desviando a
extremidade imantada da agulha no sentido oeste.
Resposta da questão 7:
a) A partícula que entrou no campo no campo magnético tem carga nula, pois não sofreu desvio:
Q  0.
b) Pela regra da mão direita, as cargas das partículas a e b são positivo e negativo, respectivamente.
Qa () e Qb ().
Resposta da questão 8:
Dados:
ε = 36 V, R1 = 2  , R2 = 4  , R3 = 2  , R4 = 4  e R5 = 2  .
1ª Resolução:
a) Como
R1 = R5 e R2 = R4,
o circuito apresenta simetria, ou seja:
i1 = i5 e i2 = i4.
Assim, podemos transformar o circuito da Fig. 1 no circuito da Fig. 2, fazendo:
i1 = i5 = x;
i2 = i4 = y;
i3 = z.
Aplicando a lei dos nós em B:
x=y+z
z = x – y (I).
Aplicando a lei das malhas:
Malha MABCNM  R1 x + R2 y –  = 0 
2 x + 4 y = 36 (II).
Malha ABEFA  R1 X + R3 z – R4 y = 0 
2 x + 2 z – 4 y = 0 (III).
Substituindo (I) em (III):
2 x + 2(x – y) – 4 y = 0  2 x + 2 x – 2 y – 4 y = 0  4 x – 6 y = 0 
-2 x + 3 y = 0 (IV).
Montando
o
2 x  4 y  36

2x  3 y  0
Substituindo em (II):
sistema
com
 7 y  36  y 
(II)
36
.
7
e
(IV)
e
somando:
 36 
2 x  4    36
 7 

2 x  36 
144
7
 x
108
14
 x
54
.
7
Em (I):
zxy
54 36

7
7

z
18
.
7
Assim:
54
A;
7
36
i2 = i4 = y =
A;
7
18
i3 = z =
A.
7
i1 = i5 = x =
b) a corrente total é:
ixy
36 54

7
7
 i
90
A.
7
Aplicando a lei de Ohm-Pouillet ao circuito:
  Req i

Req 

36

90
i
7
 Req  2,8 .
2ª Resolução
Aplicando a lei dos nós:
Nó C : i  i2  i5



Nó A : i  i1  i4
 i2  i5  i1  i4 (I).
Aplicando a lei das malhas na Fig.1:
Malha MABCNM  R1 i1 + R2 i2 –  = 0
i1 + 2 i2 = 18 (II).
Malha MAFEDCNM
2 i4 + i5 = 18 (III).
 2 i1 + 4 i2 = 36 
 R4 i4 + R5 i5 –  = 0  4 i4 + 2 i5 = 36 
Igualando (II) e (III):
i1 + 2 i2 = 2 i4 + i5 (IV).

i2  i5  i1  i4
Montando o sistema com (I) e (IV): 
2 i2  i5  i1  2 i4

i2  i5   i1  i4

  2 i2  i5  i1  2 i4

i2 = i4

 i1  i5 .
A partir dessa conclusão, recaímos na 1ª solução fazendo:
i1 = i5 = x;
i2 = i4 = y;
i3 = z.
Resposta da questão 9:
–1
Dados: N = 10; D = 10 cm = 10 m; B = 10
A expressão do fluxo magnético
–2
T; f = 2 Hz.
   é:
  N B A cos  , sendo: N o número de espiras, A a área de fluxo através da espira, B a intensidade
do vetor indução magnética, e  o ângulo formado entre as linhas de indução magnética e a normal (n) ao
plano da espira, que, para a situação inicial, é nulo ( α = 0°).
Então:

 101
D2
inicial  N B
cos 0  10 102
4
4
 final  0.

O tempo considerado é para
t 
1
1
1
T

4
4 f 4  2


2

103 
 2,5  104 Wb.
4
1
1
de rotação, ou seja,
do período, que é o inverso da frequência. Assim:
4
4

t 
1
s.
8
De acordo com a lei de Faraday-Neumann, a força eletromotriz média

0  2,5  10

1
t
8
3
m  6,3  10 V.
m  
4
 2  103 V
 m 
é dada por:

Resposta da questão 10:
a) A força magnética é dada pela expressão:
FM | Q | v B sen , sendo  o ângulo formado entre os vetores v e B .
No caso, esses vetores são perpendiculares entre si. Então: θ = 90°  sen θ = 1. A expressão da
força magnética fica, então:
FM | Q | v B.
A direção e o sentido dessa força são dados pela regra da mão direita para uma carga negativa, como
indicado na figura ao lado.
b) Como se trata de movimento retilíneo e uniforme, a força elétrica deve equilibrar a força magnética,
anulando a resultante entre elas. Assim, a força elétrica deve ser vertical e para cima. Como a carga é
negativa, a força elétrica tem sentido oposto ao do campo elétrico. Assim, esse campo elétrico
deve
FM  FE
ser

vertical,
orientado
para
baixo,
E
| Q | v B  | Q |E  v  .
B
como
indica
a
figura
E 
abaixo.