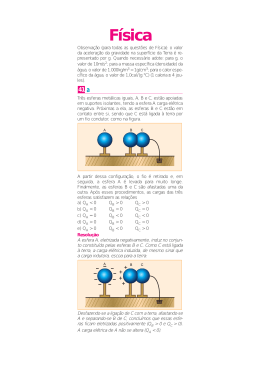
OBSERVAÇÃO (para todas as questões de
Física): o valor da aceleração da gravidade
na superfície da Terra é representado por g.
Quando necessário adote: para g, o valor de
10 m/s2 ; para a massa específica (densidade)
da água, o valor de 1.000 kg/m3 = 1g/cm3 ;
para o calor específico da água, o valor de
1,0 cal /(g. o C) (1 caloria ≅ 4 joules).
Questão 41
Três esferas metálicas iguais, A, B e C, estão
apoiadas em suportes isolantes, tendo a esfera A carga elétrica negativa. Próximas a ela,
as esferas B e C estão em contato entre si,
sendo que C está ligada à terra por um fio
condutor, como na figura.
Questão 42
No medidor de energia elétrica usado na medição do consumo de residências, há um disco,
visível externamente, que pode girar. Cada rotação completa do disco corresponde a um consumo de energia elétrica de 3,6 watt-hora.
Mantendo-se, em uma residência, apenas um
equipamento ligado, observa-se que o disco
executa uma volta a cada 40 segundos. Nesse
caso, a potência “consumida” por esse equipamento é de, aproximadamente,
A quantidade de energia elétrica de 3,6
watt-hora é definida como aquela que um
equipamento de 3,6 W consumiria se permanecesse ligado durante 1 hora.
a) 36 W
d) 324 W
b) 90 W
e) 1000 W
c) 144 W
alternativa D
A partir dessa configuração, o fio é retirado e,
em seguida, a esfera A é levada para muito
longe. Finalmente, as esferas B e C são afastadas uma da outra. Após esses procedimentos, as cargas das três esferas satisfazem as
relações
a) Q A
b) Q A
c) Q A
d) Q A
e) Q A
<
<
=
>
>
0
0
0
0
0
QB
QB
QB
QB
QB
>
=
<
>
<
0
0
0
0
0
QC
QC
QC
QC
QC
>
=
<
=
>
0
0
0
0
0
alternativa A
A configuração apresenta um processo de eletrização por indução. Com o fio ligado e na presença de A, temos elétrons indo dos corpos B e C à
Terra.
Sendo o fio retirado e, em seguida, afastado o
corpo A, teremos este com carga inalterada
(Q A < 0) e os corpos B e C com carga positiva
(QB > 0 e QC > 0 ).
Do enunciado, em cada 40 segundos a energia elétrica consumida é de 3,6 Wh = 3,6 W ⋅ 3 600 s =
= 12 960 J. Da definição de potência elétrica, temos:
12 960
∆E
P=
=
⇒ P = 324 W
∆t
40
Questão 43
Quatro ímãs iguais em forma de barra, com
as polaridades indicadas, estão apoiados sobre uma mesa horizontal, como na figura, vistos de cima.
Uma pequena bússola é também colocada na mesa, no ponto central P, eqüidistante dos ímãs, indicando a direção e o
sentido do campo
magnético dos ímãs em P. Não levando em
conta o efeito do campo magnético terrestre,
a figura que melhor representa a orientação
da agulha da bússola é
física 2
a)
b)
c)
d)
e)
a) I1 = 1,0 A
b) I1 = 1,5 A
c) I1 = 2,0 A
d) I1 = 5,0 A
e) I1 = 8,0 A
alternativa A
A agulha da bússola irá orientar-se com mesma
direção e sentido do campo magnético resultante
(BR ) no ponto P, devido aos campos (B) gerados
por cada um dos quatro ímãs, de acordo com a figura:
I2
I2
I2
I2
I2
= 2,0 A
= 3,0 A
= 4,0 A
= 3,0 A
= 4,0 A
I3
I3
I3
I3
I3
= 11 A
= 9,5 A
= 8,0 A
= 6,0 A
= 2,0 A
alternativa C
Como em uma associação em paralelo as correntes são inversamente proporcionais às resistências elétricas, esquematicamente temos o seguinte circuito elétrico:
Da Lei dos Nós, temos:
I1 + I 2 + I3 = 14 ⇒ I + 2I + 4I = 14 ⇒ I = 2 A
Portanto, I1 = 2,0 A; I 2 = 4,0 A e I3 = 8,0 A.
Questão 44
Para um teste de controle, foram introduzidos três amperímetros (A1 , A2 e A 3 ) em um
trecho de um circuito, entre M e N, por onde
passa uma corrente total de 14 A (indicada
pelo amperímetro A4 ). Nesse trecho, encontram-se cinco lâmpadas, interligadas como
na figura, cada uma delas com resistência invariável R. Nessas condições, os amperímetros A1 , A2 e A 3 indicarão, respectivamente,
correntes I1 , I2 e I 3 com valores aproximados
de
Questão 45
Um anel de alumínio, suspenso por um fio
isolante, oscila entre os pólos de um ímã,
mantendo-se, inicialmente, no plano perpendicular ao eixo N − S e eqüidistante das faces
polares. O anel oscila, entrando e saindo da
região entre os pólos, com uma certa amplitude. Nessas condições, sem levar em conta a
resistência do ar e outras formas de atrito
mecânico, pode-se afirmar que, com o passar
do tempo,
física 3
a) a amplitude de oscilação do anel diminui.
b) a amplitude de oscilação do anel aumenta.
c) a amplitude de oscilação do anel permanece constante.
d) o anel é atraído pelo pólo Norte do ímã e lá
permanece.
e) o anel é atraído pelo pólo Sul do ímã e lá
permanece.
alternativa A
Pela Lei de Lenz, durante a entrada e durante a
saída, surge uma corrente induzida no anel de
alumínio gerando neste polaridades magnéticas
que se alternam. Devido a isso, o anel será repelido durante sua entrada e atraído durante sua saída, diminuindo a amplitude de oscilação do anel.
Podemos pensar, também, que a energia do sistema é dissipada através do tempo, pela corrente
produzida na espira.
Desejando manter a folha esticada, é colocada uma placa de vidro, com 5 cm de espessura, sobre a mesma. Nesta nova situação, pode-se fazer com que a fotografia continue
igualmente nítida
a) aumentando D0 de menos de 5 cm.
b) aumentando D0 de mais de 5 cm.
c) reduzindo D0 de menos de 5 cm.
d) reduzindo D0 de 5 cm.
e) reduzindo D0 de mais de 5 cm.
alternativa A
Colocando-se a placa de vidro sobre a folha de
papel, é formada uma imagem o’, de um ponto
objeto o do desenho, conforme a figura a seguir:
Questão 46
Radiações como Raios X, luz verde, luz ultravioleta, microondas ou ondas de rádio,
são caracterizadas por seu comprimento de
onda (λ) e por sua freqüência (f). Quando essas radiações propagam-se no vácuo, todas
apresentam o mesmo valor para
a) λ
b) f
c) λ.f
d) λ/f
e) λ2 /f
alternativa C
Todas as ondas mencionadas são eletromagnéticas e possuem, no vácuo, mesma velocidade
c = 3 ⋅ 10 8 m/s dada por c = λ ⋅ f .
Questão 47
Certa máquina fotográfica é fixada a uma
distância D0 da superfície de uma mesa,
montada de tal forma a fotografar, com nitidez, um desenho em uma folha de papel que
está sobre a mesa.
Como o’ sofreu uma aproximação da máquina fotográfica, para que a câmara produza uma imagem igualmente nítida de o’, devemos afastar a
câmara de uma distância d < 5 cm, ou seja, aumentando D0 de menos de 5 cm.
Questão 48
Uma câmera de segurança (C), instalada em
uma sala, representada em planta na figura,
“visualiza” a região clara indicada.
Desejando aumentar o campo de visão da câmera, foi colocado um espelho plano, retangular, ocupando toda a região da parede entre
os pontos A e B.
física 4
Nessas condições, a figura que melhor representa a região clara, que passa a ser visualizada pela câmera, é
a)
b)
c)
d)
representa a variação da pressão que a onda
sonora exerce sobre o medidor, em função do
tempo, em µs (1 µs = 10−6 s). Analisando a tabela de intervalos de freqüências audíveis,
por diferentes seres vivos, conclui-se que esse
apito pode ser ouvido apenas por
Seres vivos
Intervalos de
Freqüência
cachorro
15 Hz – 45.000 Hz
ser humano
20 Hz – 20.000 Hz
sapo
50 Hz – 10.000 Hz
gato
60 Hz – 65.000 Hz
morcego
1000 Hz – 120.000 Hz
e)
alternativa B
A posição da imagem da câmera formada pelo
espelho e seu campo visual são dados pela propriedade da simetria, como é mostrado a seguir:
a) seres humanos e cachorros
b) seres humanos e sapos
c) sapos, gatos e morcegos
d) gatos e morcegos
e) morcegos
alternativa D
Na figura fornecida, o intervalo de tempo representado corresponde à metade do período da
T
onda, ou seja,
= 10 ⋅ 10 −6 s . Assim, temos:
2
1
1
f =
⇒f =
⇒ f = 50 000 Hz
T
2 ⋅ 10 ⋅ 10 −6
Da tabela fornecida conclui-se que esse apito
pode ser ouvido apenas por gatos e morcegos.
Assim, a região clara que passa a ser visualizada
pela câmera é melhor representada pela figura da
alternativa B.
Questão 49
O som de um apito é analisado com o uso de
um medidor que, em sua tela, visualiza o padrão apresentado na figura abaixo. O gráfico
Questão 50
Em uma estrada, dois carros, A e B, entram
simultaneamente em curvas paralelas, com
raios R A e RB . Os velocímetros de ambos os
carros indicam, ao longo de todo o trecho
curvo, valores constantes VA e VB . Se os
carros saem das curvas ao mesmo tempo, a
relação entre VA e VB é
física 5
vimento vertical uniformemente acelerado. Logo,
a figura que melhor poderia representar as posições aproximadas do avião e dos pacotes, em um
mesmo instante, é a representada na alternativa B.
Questão 52
a) VA = VB
b) VA /VB = R A / RB
2
d) VA /VB = RB / R A
c) VA /VB = (R A / RB )
e) VA /VB = (RB / R A )2
alternativa B
Como os valores das velocidades dos dois carros
são constantes e admitindo os raios constantes,
para o mesmo intervalo de tempo, temos:
∆t A = ∆tB ⇒
πR A
πRB
=
⇒
VA
VB
VA
R
= A
VB
RB
Balões estão voltando a ser considerados
como opção para o transporte de carga. Um
balão, quando vazio, tem massa de 30.000 kg.
Ao ser inflado com 20.000 kg de Hélio, pode
transportar uma carga útil de 75.000 kg.
Nessas condições, o empuxo do balão no ar
equilibra seu peso. Se, ao invés de Hélio, o
mesmo volume fosse preenchido com Hidrogênio, esse balão poderia transportar uma
carga útil de aproximadamente
a) 37.500 kg
b) 65.000 kg Nas CNTP,
c) 75.000 kg Massa de 1 mol de H2 ≅ 2,0 g
d) 85.000 kg Massa de 1 mol de He ≅ 4,0 g
e) 150.000 kg
alternativa D
Questão 51
Em decorrência de fortes chuvas, uma cidade do interior paulista ficou isolada. Um
avião sobrevoou a cidade, com velocidade horizontal constante, largando 4 pacotes de alimentos, em intervalos de tempos iguais. No
caso ideal, em que a resistência do ar pode
ser desprezada, a figura que melhor poderia
representar as posições aproximadas do avião
e dos pacotes, em um mesmo instante, é
Supondo que o balão comporta o mesmo volume,
ou seja, o mesmo número de mols de H 2 e He,
sendo a relação entre as massas de hidrogênio
m
1
, a massa to(mH ) e hélio (mHe ) igual a H =
2
mHe
1
tal de hidrogênio será mH = ⋅ 20 000 = 10 000 kg.
2
Portanto o aumento da carga útil é dado por
mHe − mH = 20 000 − 10 000 = 10 000 kg e a
carga útil (m) transportada pelo balão será m =
= 75 000 + 10 000 = 85 000 kg.
Questão 53
a)
b)
c)
d)
e)
alternativa B
Adotando o avião como referencial, cada pacote
tem velocidade horizontal nula. Assim, para o referencial adotado, cada pacote descreve um mo-
Um jovem escorrega por um tobogã aquático, com uma rampa retilínea, de comprimento L, como na figura, podendo o atrito ser
desprezado. Partindo do alto, sem impulso,
ele chega ao final da rampa com uma velocidade de cerca de 6 m/s. Para que essa velocidade passe a ser de 12 m/s, mantendo-se a
inclinação da rampa, será necessário que o
comprimento dessa rampa passe a ser aproximadamente de
física 6
e)
a) L/2
b) L
c) 1,4 L
d) 2 L
e) 4 L
alternativa E
Como a inclinação da rampa é mantida, a aceleração do jovem será a mesma nas duas situações. Assim, da Equação de Torricelli vem:
v 2 = v 02 + 2a ∆S ⇒
alternativa E
Da figura dada, temos que a quantidade de movimento do sistema formado pelos dois discos imediatamente antes da colisão (Qantes ) é dada por:
6 2 = 0 2 + 2a ⋅ L
12 2 = 0 2 + 2a ⋅ L’
Dividindo as equações, temos:
62
12 2
=
L
⇒
L’
L’ = 4L
Questão 54
Dois pequenos discos, de massas iguais, são
lançados sobre uma superfície plana e horizontal, sem atrito, com velocidades de módulos
iguais. A figura ao lado registra a posição dos
discos, vistos de cima, em intervalos de tempo sucessivos e iguais, antes de colidirem,
próximo ao ponto P. Dentre
as possibilidades representadas, aquela que pode corresponder às posições dos discos,
em instantes sucessivos, após
a colisão, é
a)
b)
Sendo o sistema formado pelos dois discos isolado, do Princípio de Conservação da Quantidade
de Movimento, temos que a quantidade de movimento do sistema imediatamente após a colisão
(Qapós ) é igual a Qantes .
Dentre as possibilidades representadas, a única
que satisfaz essa condição é a representada na
alternativa E.
Questão 55
c)
d)
Um avião, com massa M = 90 toneladas, para
que esteja em equilíbrio em vôo, deve manter
seu centro de gravidade sobre a linha vertical
CG, que dista 16 m do eixo da roda dianteira
e 4,0 m do eixo das rodas traseiras, como na
figura abaixo. Para estudar a distribuição de
massas do avião, em solo, três balanças são
colocadas sob as rodas do trem de aterrissa-
física 7
gem. A balança sob a roda dianteira indica
MD e cada uma das que estão sob as rodas
traseiras indica M T .
ND = M D ⋅ g
NT = MT ⋅ g
⇒
⇒
180 000 = M D ⋅ 10
360 000 = MT ⋅ 10
⇒
M D = 18 000 kg = 18 t
MT = 36 000 kg = 36 t
Questão 56
Uma distribuição de massas, compatível com
o equilíbrio do avião em vôo, poderia resultar
em indicações das balanças, em toneladas,
correspondendo aproximadamente a
a) MD = 0
M T = 45
b) MD = 10
M T = 40
c) MD = 18
M T = 36
d) MD = 30
M T = 30
e) MD = 72
M T = 9,0
alternativa C
Estando o avião apoiado em uma balança na
roda dianteira e em duas balanças nas rodas traseiras, as forças que atuam sobre ele são dadas
por:
Satélites utilizados para telecomunicações
são colocados em órbitas geoestacionárias ao
redor da Terra, ou seja, de tal forma que
permaneçam sempre acima de um mesmo
ponto da superfície da Terra. Considere algumas condições que poderiam corresponder
a esses satélites:
I. ter o mesmo período, de cerca de 24 horas
II. ter aproximadamente a mesma massa
III. estar aproximadamente à mesma altitude
IV. manter-se num plano que contenha o círculo do equador terrestre
O conjunto de todas as condições, que satélites em órbita geoestacionária devem necessariamente obedecer, corresponde a
a) I e III
b) I, II, III
c) I, III e IV
d) II e III
e) II, IV
alternativa C
I. Correta. Os satélites geoestacionários possuem
velocidades angulares iguais à da Terra, portanto,
o mesmo período, de cerca de 24 horas.
II. Errada. O movimento orbital de um satélite independe de sua massa.
III. Correta. Por terem o mesmo período, da Terceira Lei de Kepler, eles devem estar aproximadamente à mesma altitude.
IV. Correta. Os satélites geoestacionários devem
manter-se num plano que contenha o círculo do
equador terrestre, a fim de permanecerem sempre acima de um mesmo ponto da superfície da
Terra.
Das condições de equilíbrio, vem:
R =0
ΣM (CG) = 0 ⇒
P = Mg
ND + 2NT = P
⇒ ND ⋅ 16 = 2NT ⋅ 4
⇒
P = 90 000 ⋅ 10 = 900 000 N
⇒
⇒
ND + 2NT = 900 000
2ND = NT
⇒
ND = 180 000 N
NT = 360 000 N
Assim, as indicações M D e MT das balanças são
dadas por:
Questão 57
Em um processo industrial, duas esferas de
cobre maciças, A e B, com raios R A = 16 cm e
RB = 8 cm, inicialmente à temperatura de
20o C, permaneceram em um forno muito
quente durante períodos diferentes. Constatou-se que a esfera A, ao ser retirada, havia
física 8
atingido a temperatura de 100o C. Tendo ambas recebido a mesma quantidade de calor, a
esfera B, ao ser retirada do forno, tinha temperatura aproximada de
a) 30o C
b) 60o C
c) 100o C
o
o
d) 180 C
e) 660 C
alternativa E
Sendo iguais as quantidades de calor recebidas
pelas esferas (QB = Q A ), da Equação Fundamental da Calorimetria e da definição de massa
específica (µ), temos:
Q = mc∆θ
QB = Q A ⇒
m = µ ⋅V
⇒ mB ⋅ c ⋅ ( θB − 20) = m A ⋅ c ⋅ (100 − 20) ⇒
⇒ µ ⋅ VB ⋅ ( θB − 20) = µ ⋅ VA ⋅ 80 ⇒
4
4
3
⇒
π ⋅ RB3 ( θB − 20) =
π ⋅ RA
⋅ 80 ⇒
3
3
Q = mc∆θ
⇒ Q = µ ⋅ V ⋅ c ⋅ ∆θ ⇒
m = µV
⇒ Q = 1 000 ⋅ 200 ⋅ 4(45 − 10) ⇒ Q = 2,8 ⋅ 107 J
Para o aquecimento da água obtido através do
gerador, temos:
P ⋅ ∆t = Q ⇒
⇒ ∆t =
U2
Q ⋅R
⋅ ∆t = Q ⇒ ∆t =
⇒
R
U2
2,8 ⋅ 107 ⋅ 11
110 2
⇒ ∆t = 2,5 ⋅ 10 4 s
Sendo o consumo de gasolina (C) do gerador igual
1,0
l
a C =
⋅ , o volume (V) de gasolina
3
s
3,6 ⋅ 10
1,0
será dado por V = C ⋅ ∆t =
⋅ 2,5 ⋅ 10 4 = 7 l.
3,6 ⋅ 10 3
Portanto o consumo de gasolina obtido através do
gerador, quando comparado ao da combustão, é
aproximadamente 7 vezes maior.
⇒ 8 3 ( θB − 20) = 16 3 ⋅ 80 ⇒ θB = 660 o C
Questão 58
Usando todo o calor produzido pela combustão direta de gasolina, é possível, com 1,0 litro de tal produto, aquecer 200 litros de
água de 10o C a 45o C. Esse mesmo aquecimento pode ser obtido por um gerador de
eletricidade, que consome 1,0 litro de gasolina por hora e fornece 110 V a um resistor de
11 Ω, imerso na água, durante um certo intervalo de tempo. Todo o calor liberado pelo
resistor é transferido à água. Nessas condições, o aquecimento da água obtido através
do gerador, quando comparado ao obtido diretamente a partir da combustão, consome
uma quantidade de gasolina, aproximadamente,
a) 7 vezes menor
b) 4 vezes menor
c) igual
d) 4 vezes maior
e) 7 vezes maior
Questão 59
Um equipamento possui um sistema formado
por um pistão, com massa de 10 kg, que se
movimenta, sem atrito, em um cilindro de
secção transversal S = 0,01 m2 . Operando em
uma região onde a pressão atmosférica é de
10,0 x 104 Pa (1 Pa = 1 N/m2 ), o ar aprisionado no interior do cilindro mantém o pistão a
uma altura H = 18 cm. Quando esse sistema
é levado a operar em uma região onde a pressão atmosférica é de 8,0 x 104 Pa, mantendo-se a mesma temperatura, a nova altura H
no interior do cilindro passa a ser aproximadamente de
alternativa E
Sendo a massa específica (µ) da água igual a
g
1 000
e utilizando a Equação Fundamental da
l
Calorimetria, para a combustão direta da gasolina, temos:
a) 5,5 cm
d) 22 cm
b) 14,7 cm
e) 36 cm
c) 20 cm
física 9
alternativa D
A pressão sobre o gás corresponde à soma da
pressão atmosférica local mais a pressão devido
ao peso do pistão. Sendo a transformação isotérmica, da Lei de Boyle-Mariotte e da definição de
pressão, temos:
 mg

+ 8,0 ⋅ 10 4  ⋅ H ⋅ S =
p 2 ⋅ V2 = p1 ⋅ V1 ⇒ 
 S

 mg
4
= 
+ 10,0 ⋅ 10  ⋅ 18 ⋅ S ⇒
 S

 10 ⋅ 10

⇒
+ 8,0 ⋅ 10 4  ⋅ H =
 0,01

 10 ⋅ 10
4
= 
+ 10,0 ⋅ 10  ⋅ 18 ⇒
 0,01

⇒ H = 22 cm
Questão 60
Em 1987, devido a falhas nos procedimentos
de segurança, ocorreu um grave acidente em
Goiânia. Uma cápsula de Césio-137, que é radioativo e tem meia-vida de 30 anos, foi sub-
traída e violada, contaminando pessoas e o
ambiente. Certa amostra de solo contaminado, colhida e analisada na época do acidente,
foi recentemente reanalisada. A razão R, entre a quantidade de Césio-137, presente hoje
nessa amostra, e a que existia originalmente,
em 1987, é
A meia-vida de um elemento radioativo é
o intervalo de tempo após o qual o número
de átomos radioativos existentes em certa
amostra fica reduzido à metade de seu valor inicial.
a) R = 1
c) R = 0,5
e) R = 0
b) 1 > R > 0,5
d) 0,5 > R > 0
alternativa B
Sendo o intervalo de tempo decorrido entre 1987
e 2001 menor que 30 anos, da definição de meiavida temos que a razão R entre a quantidade de
Césio-137 presente hoje nessa amostra e a que
existia originalmente em 1987 é menor que 1 e
maior que 0,5.