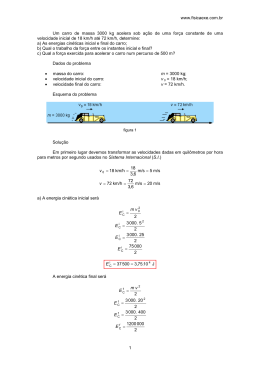
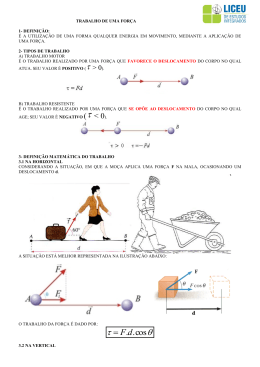
1
Referência: Sears e Zemansky – Física I – Mecânica
Capítulo 6: TRABALHO E ENERGIA CINÉTICA
Resumo: Profas. Bárbara e Márcia
1. INTRODUÇÃO
A importância do conceito de energia se baseia no princípio da conservação da
energia: a energia é uma grandeza que pode ser convertida de uma forma para outra,
mas que não pode ser criada nem destruída. Por exemplo, no motor de um automóvel, a
energia química armazenada no combustível é convertida parcialmente em energia
térmica e parcialmente em energia mecânica que acelera o automóvel. Nesse e em outros
processos, a energia total permanece constante, ou seja, a soma de todas as formas de
energia envolvidas permanece a mesma. Neste capítulo estudaremos a energia cinética,
ou energia do movimento e como ela se relaciona com o conceito de trabalho.
2. TRABALHO REALIZADO POR UMA FORÇA CONSTANTE
F
Direção do deslocamento
θ
•
Embora existam outras forças atuando no corpo que se desloca, estamos
calculando apenas o trabalho executado pela força F.
θ
Direção do deslocamento
O Trabalho (W) realizado pela força F constante sobre a caixa é definido pela expressão:
W = F .s. cos θ = F .s
Onde F e s são os módulos dos vetores F( força que realiza o trabalho)
(deslocamento do corpo enquanto a força F estiver agindo ).
e
s
Observações:
•
Unidades de medida de Trabalho
Unidade SI
newton-metro ( N.m )
joule (J)
1 J é o trabalho realizado por uma força de módulo 1 N que atua num corpo que se
desloca em 1 m.
•
Justificativa:
2
A palavra Trabalho usada para definir esta grandeza física é consistente com o
significado da palavra usada no cotidiano, pois alguém contribuiu de certa forma com
um “esforço” para realizar o deslocamento.
SINAIS DO TRABALHO
a) θ é ângulo agudo :
0 ≤ θ < 90 o
b) θ é ângulo reto :
θ = 90 o
Trabalho W +
Trabalho W = 0
c) θ é ângulo obtuso :
90 o < θ ≤ 180
Trabalho W -
3. TRABALHO REALIZADO POR VÁRIAS FORÇAS
Exemplo 01:
José deseja impressionar Elaine com seu novo carro, porém o carro morre no meio de um
cruzamento. Enquanto Elaine gira o volante, José empurra o carro 19m para desimpedir o
cruzamento. Sabendo que ele empurra o carro com uma força de 210 N na mesma
direção e no mesmo sentido do deslocamento, qual é o trabalho realizado por esta força
sobre o carro?
Exemplo 02:
O Fazendeiro Johnson amarra seu trator a um trenó carregado de madeira e o puxa até
uma distância de 20m ao longo de um terreno horizontal com neve. O peso total do trenó
carregado é igual a 14700 N. O trator exerce uma força constante de 5000N formando um
ângulo de 36,9º. Acima da horizontal, como indicado. Existe uma força de atrito de 3500
N que se opõe ao movimento. Calcule o trabalho que cada força realiza sobre o trenó e o
trabalho total realizado por todas as forças.
3
4. TEOREMA DO TRABALHO-ENERGIA CINÉTICA
Demonstração: (em sala)
1
K = .m.v 2 ( definição de energia cinética)
2
K = energia cinética
m = massa
v = velocidade
“ A energia cinética de uma partícula é igual ao trabalho total realizado para acelerá-lo
a partir do repouso até sua velocidade presente.”
WTOT = K 2 − K 1 = ∆K (teorema do trabalho-energia)
Observações: 1. Quando W tot é positivo, K2 é maior que K1, a energia cinética aumenta
e a velocidade final da partícula é maior do que sua velocidade inicial. Quando W tot é
negativo, K2 é menor que K1, a energia cinética diminui e a velocidade final da
partícula é menor do que sua velocidade inicial. Quando W tot = 0, a energia cinética
final K2 é igual a K1 e a velocidade não se altera.
2. Referencial inercial
3. Demonstramos o teorema para o caso especial do movimento retilíneo uniforme,
mas ele é válido mesmo quando as forças não são constantes e a trajetória é uma
curva.
Exemplo 03:
Examinando novamente o trenó do exercício anterior. Encontramos para o trabalho
total de todas as forças o valor 10000J = 10KJ, de modo que a energia cinética do
trenó aumentou de 10 KJ, a massa do trenó é 1500 Kg. Suponha que a velocidade
inicial v1=2 m/s. Qual é sua velocidade final v2?
5. TRABALHO E ENERGIA COM FORÇAS VARIÁVEIS
Um exemplo de trabalho e energia com forças variáveis seria o caso de
deformação de molas. Para esticar uma mola de uma distância x além de sua posição
não deformada, devemos aplicar uma força F em cada uma de suas extremidades
(Figura 6.13). Quando o alongamento x não é muito grande, verifica-se que o módulo
F é diretamente proporcional ao módulo do deslocamento x:
F = k .x (força necessária para esticar a mola)
onde k é a constante da mola
4
Graficamente podemos observar na figura 6.14 que o trabalho total realizado pela
força é igual a área abaixo da curva:
1
W = .k .x 2
2
Exemplo 4: Uma mulher pesando 600N está em pé sobre uma balança de mola
contendo uma mola dura. No equilíbrio, a mola está comprimida 1,0 cm sob a ação do seu
peso. Calcule a constante da mola e o trabalho total realizado pela força de compressão
sobre a mola.
5. POTÊNCIA
Na maioria das vezes o cálculo do trabalho que um sistema realiza não é tão importante,
mas sim a rapidez com que um determinado trabalho é realizado pelo sistema. Define-se
então uma grandeza que represente a variação temporal do Trabalho. Essa grandeza é
denominada Potência média do sistema, e expresso por:
∆W
medida em
∆t
Também são ainda utilizadas as unidades:
P=
Potência Média :
•
•
Cavalo-vapor - cv
Horsepower - hp
-
J
= W ( watt)
s
1 cv = 735,5 W
1 hp = 746 W
Relação entre Potência Média e Velocidade :
Na mecânica podemos escrever a potência em função da força e da velocidade.
P = F .v med
5
Exemplo 05:
Como parte de uma campanha para angariar fundos para uma instituição de caridade,
uma velocista de Chicago com massa de 50 Kg sobe correndo as escadas da Torre Sears
em Chicago, o edifício mais alto dos EUA com altura de 443 m. Para que ela atinja o topo
em 15 minutos, qual deve ser sua potência média em Watts? E em quilowatts?
Exercícios para entregar no dia da prova:
1. Um velho balde de carvalho com massa igual a 6,75 Kg está pendurado em um
poço na extremidade de uma corda. A corda passa sobre uma polia sem atrito no
topo do poço, e você puxa horizontalmente a extremidade da corda para elevar
lentamente o balde até uma altura de 4 m. a) Qual o trabalho realizado pela sua
força ao puxar o balde para cima? b) Qual o trabalho realizado pela força de
gravidade sobre o balde? c) Qual o trabalho total realizado pelo balde?
2. a) Calcule a energia cinética, em joules, de um automóvel de 1600 Kg viajando a
13,88 m/s. b) Qual é o fator da variação da energia cinética quando a velocidade
dobra?
3. Seu trabalho é colocar em um caminhão engradados de 30 Kg, elevando-os 0,90m
do chão até o caminhão. Quantos engradados você coloca no caminhão em um
minuto supondo que sua potência média seja de 100 W?
4. Um martelo de um bate-estaca pesa 3800N e deve ser elevado verticalmente
2,80m com velocidade constante durante um intervalo de 4s. Qual é a potência em
watts e em c.v. que o motor deve fornecer ao martelo?
Respostas:
1. a) 246,6J b) - 246,6J c) =0 (nulo)
2. a) 154123,5J ou 1,5x105J
b) 4 vezes maior
3. 23 engradados
4. 2660 W ou 3,6 c.v.