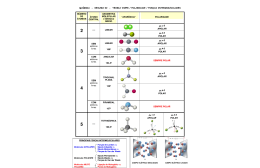
Aula 20: Métodos de Resposta em Freqüência: Gráficos Polares. Gráficos do logmódulo versus fase.
3. GRÁFICOS POLARES
O gráfico polar de uma função de transferência senoidal G ( jω ) é um gráfico do
módulo de G ( jω ) versus o ângulo de fase de G ( jω ) em coordenadas polares, conforme ω
é variado desde zero até infinito. Portanto, o gráfico polar é o lugar dos vetores G ( jω )
∠G ( jω ) conforme ω varia de zero a infinito. Observe que, em gráficos polares, um
ângulo de fase positivo (negativo) é medido no sentido anti-horário (horário) em relação ao
eixo real positivo. O gráfico polar é muitas vezes denominado gráfico de Nyquist. Um
exemplo deste tipo de gráfico é indicado na Fig. 21. Cada ponto no gráfico polar de G ( jω )
representa o ponto terminal de um vetor, para um particular valor de ω . No gráfico polar é
importante indicar a graduação em freqüência do lugar geométrico. As projeções de G ( jω )
sobre os eixos real e imaginário correspondem às suas componentes real e imaginária.
Tanto o módulo, G ( jω ) , como o ângulo de fase, ∠G ( jω ) , devem ser calculados
diretamente para cada freqüência ω na construção dos gráficos polares. Como o gráfico
logarítmico é fácil de construir, entretanto, os dados necessários para a construção do
gráfico polar podem ser obtidos diretamente do gráfico logarítmico, se este último for
desenhado inicialmente e os decibéis forem convertidos em módulos comuns pelo uso da
Fig. 6.
Fig. 21 – Gráfico Polar.
Para dois sistemas ligados em cascata, a função de transferência global da
combinação, na ausência de efeitos de carga, é o produto das duas funções de transferência
individuais. Se for necessária a multiplicação de duas funções de transferência senoidais,
isto pode ser realizado multiplicando-se, para cada freqüência, as funções de transferências
143
senoidais individuais por meio da multiplicação de álgebra-complexa. Isto é, se G ( jω ) =
G1 ( jω )G2 ( jω ) , então
G ( jω ) = G ( jω ) ∠G 2 ( jω ) ,
onde
G ( jω ) = G1 ( jω ) G2 ( jω )
e
∠G ( jω ) = ∠G1 ( jω ) + ∠G2 ( jω ) .
O produto de G1 ( jω ) e G2 ( jω ) é indicado na Fig. 22.
Em geral, se for desejado um gráfico polar de G1 ( jω )G2 ( jω ) , é conveniente
desenhar primeiro um gráfico logarítmico de G1 ( jω )G2 ( jω ) e então converter em um
gráfico polar ao invés de desenhar os gráficos polares de G1 ( jω ) e G2 ( jω ) e multiplicar
estes dois no plano complexo para obter um gráfico polar de G1 ( jω )G2 ( jω ) .
Uma vantagem no uso do gráfico polar é que ele mostra as características de
resposta em freqüência de um sistema, em toda a faixa de freqüência, em um único gráfico.
Uma desvantagem é que o gráfico não indica claramente as contribuições de malha-aberta.
Fig. 22 – Gráficos Polares de G1 ( jω ) , G2 ( jω ) e G1 ( jω )G2 ( jω ) .
Fatores integral e derivativo ( jω )
1
O gráfico polar de G ( jω ) = 1 / jω é o eixo imaginário negativo, uma vez que
144
G ( jω ) =
1
1 1
= − j = ∠ − 90 o .
ω ω
jω
O gráfico polar de G ( jω ) = jω é o eixo imaginário positivo.
Fatores de primeira-ordem (1 + jωτ )
1
Para a função de transferência senoidal
G ( jω ) =
1
1
=
∠ − tan −1ωτ ,
2
2
1 + jωτ
1+ω τ
os valores de G ( jω ) em ω = 0 e ω = 1 / τ são, respectivamente,
G ( j 0) = 1∠0 o
e
1
 1
G j  =
∠ − 45 o .
2
 τ
Se ω tende a infinito, o módulo de G ( jω ) tende a zero e o ângulo de fase tende a
– 90 . O gráfico polar desta função de transferência é uma semicircunferência1 conforme a
freqüência ω varia desde zero até infinito, conforme a Fig. 23(a). O centro está localizado
no ponto 0,5 sobre o eixo real e o raio é igual a 0,5.
Para demonstrar que o gráfico polar é uma semicircunferência, definimos
o
G ( jω ) = X + jY ,
onde
1
= parte real de G ( jω )
1 + ω 2τ 2
− ωτ
Y=
= parte imaginária de G ( jω )
1 + ω 2τ 2
X =
Então, obtemos
 1 1 − ω 2τ 2   − ωτ   1 
1

2

+
+
=
X
−
Y
=  .


2 2 
2 2 
2

 2 1+ ω τ  1+ ω τ   2 
2
2
1
N. do T.: No texto original em inglês, o autor refere-se a este lugar geométrico como um círculo em todo o
texto, porém, criteriosamente, deveria considerar apenas a circunferência. Conseqüentemente, utilizaremos
nesta tradução a designação deste lugar geométrico por circunferência.
145
Fig. 23 – (a) Gráfico polar de 1 / (1 + jωτ ) ; (b) Gráfico de G ( jω ) no plano X-Y.
Portanto, no plano X-Y, G ( jω ) é uma circunferência com centro em X = 1/2, Y =
0 e com raio 1/2, conforme indicado na Fig. 23(b). A semicircunferência inferior
corresponde a 0 ≤ ω ≤ ∞ e a semicircunferência superior corresponde a − ∞ ≤ ω ≤ 0 .
O gráfico polar da função de transferência 1 + jωτ é simplesmente a metade
superior da reta passando pelo ponto (1, 0) no plano complexo e paralela ao eixo imaginário
conforme a Fig. 24.2 O gráfico polar de 1 + jωτ possui uma aparência completamente
diferente daquela de 1 / (1 + jωτ ) .
Fig. 24 - Gráfico polar de 1 + jωτ .
[
Fatores quadráticos 1 + 2ζ ( jω / ω n ) + ( jω / ω n )
]
2 1
As partes de baixa-freqüência e alta-freqüência do gráfico polar para a seguinte
função de transferência senoidal
G ( jω ) =
(ζ
1
 ω   ω 
 +  j

1 + 2ζ  j
 ωn   ωn 
2
> 0) ,
são dadas, respectivamente, por
lim G ( jω ) = 1∠0 o
ω →0
2
e
N. do T. O autor está considerando apenas
lim G ( jω ) = 0∠ − 180 o .
ω →∞
ω ≥0.
146
O gráfico polar desta função de transferência senoidal tem início em 1∠0 o e
termina em 0∠ − 180 o conforme ω aumenta desde zero até infinito. Portanto, a parte de
alta-freqüência de G ( jω ) é tangente ao eixo real negativo. Os valores de G ( jω ) no
intervalo de freqüência de interesse podem ser calculados diretamente ou usando-se o
gráfico logarítmico.
Exemplos de gráficos polares da função de transferência considerada são
indicados na Fig. 25. A forma exata de um gráfico polar depende do valor da relação de
amortecimento, ζ , porém, a forma geral do gráfico é a mesma tanto para o caso
subamortecido (1 > ζ > 0) como para o caso superamortecido (ζ > 1) .
Fig. 25 – Gráficos polares de
1
 ω   ω 
 +  j

1 + 2ζ  j
 ωn   ωn 
2
,
(ζ
> 0) .
Para o caso subamortecido em ω = ω n , tem-se que G ( jω n ) = 1 / ( j 2ζ ) e o ângulo
de fase em ω = ω n é –90o. Além disso, pode ser observado que a freqüência na qual o lugar
geométrico de G ( jω ) intercepta o eixo imaginário é a freqüência natural não amortecida,
ω n . No gráfico polar, o ponto de freqüência cuja distância à origem é máxima, corresponde
à freqüência de ressonância ω r . O valor de pico de G ( jω ) é obtido pela relação entre o
módulo do vetor na freqüência de ressonância ω r e o módulo do vetor em ω = 0 . A
freqüência de ressonância ω r é indicada no gráfico polar mostrado na Fig. 26.
Para o caso superamortecido, conforme ζ aumenta bem além da unidade, o lugar
geométrico de G ( jω ) aproxima-se de uma semicircunferência. Isto pode ser observado
pelo fato de que para um sistema muito amortecido as raízes características são reais e uma
delas é muito menor que a outra. Desde que para ζ suficientemente grande o efeito da raiz
muito maior na resposta resulta muito pequeno, o sistema comporta-se como de primeira
ordem.
147
Fig. 26 – Gráfico polar mostrando o pico de ressonância e freqüência de ressonância ω r .
Para a função de transferência senoidal
 ω   ω 
 +  j

G ( jω ) = 1 + 2ζ  j
ω
ω
n 
n 


2
 ω   2ζω 
 ,
= 1 − 2  + j 
 ωn   ωn 
2
a parte em baixa freqüência da curva é
lim G ( jω ) = 1∠0 o
ω →0
e parte em alta freqüência é
lim G ( jω ) = 0∠ − 180 o .
ω →∞
Desde que a parte imaginária de G ( jω ) é positiva para ω > 0 e monotonicamente
crescente e a parte real de G ( jω ) é monotonicamente decrescente da unidade, a forma
geral do gráfico polar de G ( jω ) é conforme indicada na Fig. 27. O ângulo de fase está
entre 0o e 180o.
2
 ω   ω 
 +  j
 ,
(ζ > 0) .
Fig. 27 - Gráfico polar de 1 + 2ζ  j
 ωn   ωn 
_________________
Exemplo 4 Considere a seguinte função de transferência de segunda-ordem:
148
G (s ) =
1
.
s (τs + 1)
Esboce um gráfico polar desta função de transferência.
Uma vez que a função de transferência senoidal pode ser escrita
G ( jω ) =
1
jω (1 + jωτ )
1
τ
=−
−j
,
2 2
1+ ω τ
ω (1 + ω 2τ 2 )
a parte em baixa freqüência do gráfico polar torna-se
lim G ( jω ) = −τ − j∞ = ∞∠ − 90 o ,
ω →0
e parte em alta freqüência torna-se
lim G ( jω ) = 0 − j 0 = 0∠ − 180 o .
ω →∞
A forma geral do gráfico polar de G ( jω ) é indicada na Fig. 28. O gráfico de
G ( jω ) é assintótico para a reta vertical passando pelo ponto (− τ ,0) . Desde que a esta
função de transferência envolve a integração (1/s), a forma geral do gráfico polar difere
substancialmente daquelas correspondentes a funções de transferência de segunda ordem
que não possuem a integração.
Fig. 28 - Gráfico polar de 1 / [ jω (1 + jωτ )] .
Atraso de transporte
O atraso de transporte
G ( jω ) = e − jωτ
pode ser escrito
149
G (ωτ ) = 1∠(cosωτ − jsenωτ ) .
Desde que o módulo de G ( jω ) é sempre unitário e o ângulo de fase varia
linearmente com ω , o gráfico polar do atraso de transporte é uma circunferência unitária,
conforme indicada na Fig. 29.
Fig. 29 - Gráfico polar do atraso de transporte.
Em baixas freqüências o atraso de transporte e − jωτ e o atraso de primeira ordem
1 / (1 + jωτ ) se comportam similarmente, conforme é mostrado na Fig. 30. Os gráficos
polares de e − jωτ e 1 / (1 + jωτ ) são tangentes entre si na freqüência ω = 0 . Esse resultado
pode ser comprovado pelo fato de que, para ω << 1 / τ ,
e − jωτ ≅ 1 − jωτ
e
1
≅ 1 − jωτ .
1 + jωτ
Para ω >> 1 / τ , entretanto, existe uma diferença essencial entre e − jωτ
1 / (1 + jωτ ) , como pode ser visto na Fig. 30.
Fig. 30 - Gráficos polares de e − jωτ e 1 / (1 + jωτ ) .
_________________
Exemplo 5 Obtenha o gráfico polar da seguinte função de transferência
G ( jω ) =
e − jωL
1 + jωτ
150
e
Desde que G ( jω ) pode ser escrita
G ( jω ) = e − jωL
1
,
1 + jωτ
o módulo e o ângulo de fase são, respectivamente,
G ( j ω ) = e − j ωL
1
1
=
,
1 + jωτ
1 + ω 2τ 2
e
∠G ( jω ) = ∠e − jωL + ∠
1
= −ωL − tan −1ωτ .
1 + jωτ
Uma vez que o módulo diminui monotonicamente desde a unidade e o ângulo de
fase também diminui monotônica e indefinidamente, o gráfico polar da função de
transferência em estudo é uma espiral, conforme indicado na Fig. 31.
Fig. 31 - Gráfico polar de e − jωL / (1 + jωτ ) .
Formas gerais de gráficos polares
Os gráficos polares de uma função de transferência da forma
G ( jω ) =
K (1 + jωτ a )(1 + jωτ b )
( jω )λ (1 + jωτ 1 )(1 + jωτ 2 )
m
m −1
b0 ( jω ) + b1 ( jω ) + =
,
n
n −1
a0 ( jω ) + a1 ( jω ) + onde o grau do polinômio do denominador é maior do que o grau do polinômio do
numerador, apresentarão as seguintes formas gerais:
151
1. Para λ = 0 ou sistemas tipo 0: O ponto inicial do gráfico polar (que
corresponde a ω = 0 ) é finito e está sobre o eixo real positivo. A tangente do
gráfico polar em ω = 0 é perpendicular ao eixo real. O ponto final, que
corresponde a ω = ∞ , corresponde à origem, e a curva é tangente a um dos
eixos.
2. Para λ = 1 ou sistemas tipo 1: O termo jω no denominador contribui com 90o para o ângulo de fase total de G ( jω ) para 0 ≤ ω ≤ ∞ . Em ω = 0 , o
módulo de G ( jω ) é infinito, e o ângulo de fase resulta -90o. Em baixas
freqüências, o gráfico polar é assintótico a uma reta paralela ao eixo
imaginário negativo. Em ω = ∞ , o módulo toma-se nulo e a curva converge
para a origem e é tangente a um dos eixos.
2
3. Para λ = 2 ou sistemas tipo 2: O termo ( jω ) no denominador contribui com
-180o para o ângulo de fase total de G ( jω ) para 0 ≤ ω ≤ ∞ . Em ω = 0 , o
módulo de G ( jω ) é infinito, e o ângulo de fase é igual a -180o. Em baixas
freqüências, o gráfico polar é assintótico a uma reta paralela ao eixo real
negativo. Em ω = ∞ , o módulo torna-se nulo e a curva é tangente a um dos
eixos.
Os formatos gerais das partes de baixa-freqüência dos gráficos polares de sistemas
tipo 0, tipo 1 e tipo 2 são indicados na Fig. 32. Pode ser visto que, se o grau do polinômio
do denominador de G ( jω ) é maior do que o do numerador, então os lugares geométricos
de G ( jω ) convergem para a origem no sentido horário. Em ω = ∞ , os lugares geométricos
são tangentes a um ou ao outro eixo, conforme indicado na Fig. 33.
Fig. 32 - Gráficos polares de sistemas tipo 0, tipo 1 e tipo 2.
G ( jω ) =
b0 ( jω ) + m
a 0 ( jω ) + n
Fig. 33 - Gráficos polares na faixa de alta freqüência.
152
Para o caso em que os graus dos polinômios do denominador e do numerador de
G ( jω ) são os mesmos, o gráfico polar tem início a uma distância finita sobre o eixo real e
termina em um ponto finito sobre o eixo real.
Note que quaisquer formas complicadas nas curvas do gráfico polar são causadas
pela dinâmica do numerador, isto é, pelas constantes de tempo no numerador da função de
transferência. A Fig. 34 fornece exemplos de gráficos polares de funções de transferência
com dinâmicas no numerador. Na análise de sistemas de controle, o gráfico polar de
G ( jω ) na faixa de freqüência de interesse deve ser precisamente determinado.
Fig. 34 - Gráficos polares de funções de transferência com dinâmica no numerador.
A Tabela 1 mostra esboços de gráficos polares para algumas funções de
transferência.
4. GRÁFICOS DO LOG-MÓDULO VERSUS FASE
Uma outra abordagem para retratar graficamente as características de resposta em
freqüência é usar o gráfico do log-módulo versus fase, que é um gráfico do logaritmo do
módulo em decibéis versus o ângulo de fase, ou margem de fase, para uma faixa de
freqüência de interesse (a margem de fase é a diferença entre o ângulo de fase real φ e 180o; isto é, φ − (− 180 o ) = 180 o + φ ). A curva é graduada em termos da freqüência ω .
Estes gráficos do log-módulo versus fase são algumas vezes denominados gráficos de
Nichols.
No diagrama de Bode, as características de resposta em freqüência de G ( jω ) são
fornecidas em um papel monolog por meio de duas curvas separadas, a curva do logmódulo e a curva do ângulo de fase, enquanto no gráfico do log-módulo versus fase, as
duas curvas do diagrama de Bode são combinadas em apenas uma. O gráfico do logmódulo versus fase pode ser facilmente construído pelos valores obtidos do logaritmo do
módulo e do ângulo de fase a partir do diagrama de Bode. Note que no gráfico do logmódulo versus fase, uma variação na constante de ganho de G ( jω ) simplesmente desloca a
curva para cima (para ganhos crescentes) ou para baixo (para ganho decrescente), porém a
forma da curva permanece a mesma.
153
As vantagens do gráfico do log-módulo versus fase são que a estabilidade relativa
do sistema de malha-fechada pode ser determinada rapidamente e que a compensação pode
ser realizada com facilidade.
Tabela 1 – Gráficos polares de funções de transferência simples
Os gráficos do log-módulo versus fase para as funções de transferência senoidais
G ( jω ) e 1 / G ( jω ) são anti-simétricos em relação à origem desde que
1
em db = − G ( jω ) em db
G ( jω )
e
154
1
= −∠G ( jω ) .
G ( jω )
Desde que as características do log-módulo e do ângulo de fase das funções de
transferência básicas foram discutidas com detalhes nas Seções 2 e 3, aqui será suficiente
fornecer exemplos de alguns gráficos do log-módulo versus fase. A Tabela 2 mostra estes
exemplos.
∠
Tabela 2 – Gráficos log-módulo versus fase de funções de transferência simples
A Fig. 35 compara as curvas de resposta em freqüência de
G ( jω ) =
1
 ω   ω 
 +  j

1 + 2ζ  j
 ωn   ωn 
2
155
nas três representações diferentes. No gráfico log-módulo versus fase a distância vertical
entre os pontos correspondentes a ω = 0 e ω = ω r , onde ω r é a freqüência de ressonância,
é o valor de pico de G ( jω ) em decibéis.
Fig. 35 – Três representações da resposta em freqüência de
2
1 / 1 + 2ζ ( jω / ω n ) + ( jω / ω n ) , (ζ > 0) . (a) gráfico logarítmico; (b) gráfico polar e (c)
gráfico log-módulo versus fase.
[
]
156