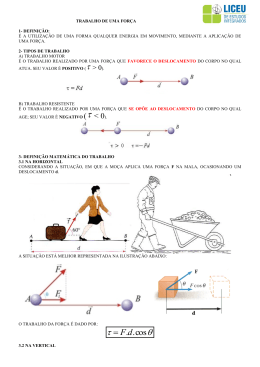
Polícia Rodoviária Federal
Prof. Dirceu Pereira
Física
Aulas 4 e 5 de 5
UNIDADE 5 – OS PRINCÍPIOS DA CONSERVAÇÃO
Assim, temos que: τ = ±F ⋅ cos θ ⋅ ∆S
5.1. TRABALHO, POTÊNCIA E RENDIMENTO
Atentar que F ⋅ senθ ≤ P
5.1.1. TRABALHO
Em Física, o termo trabalho, designado pela letra grega
τ (tau), está associado a forças, e não a corpos: diz-se
“trabalho de uma força” e nunca “trabalho de um corpo”.
Desde já, vamos afirmar que:
a) o trabalho será sempre de uma força;
b) o trabalho é realizado num deslocamento entre dois
pontos provocado pela resultante das forças aplicadas
ao corpo;
c) o trabalho é uma grandeza física escalar;
d) o trabalho depende do referencial;
e) o trabalho será positivo quando a força favorece o
deslocamento; neste caso, é chamado de trabalho
motor;
f) o trabalho será negativo quando a força se opõe ao
deslocamento; neste caso, é chamado de trabalho
resistente.
Situação 1
Veja a figura 1. Se uma força resultante F é constante e
paralela ao deslocamento do bloco, definimos trabalho
de uma força ao produto da força resultante pela
variação do deslocamento. Assim:
τ = ±F ⋅ ∆S
Se θ = 0º τ = ±F ⋅ ∆S
Se θ = 90º τ = 0
Também podemos calcular o trabalho através da área do
gráfico (figura 4).
Situação 3
No caso específico da força-peso, o deslocamento será
vertical.
τ = ±P ⋅ ∆h
Se o corpo está em queda, o peso está a favor do
deslocamento e o trabalho é motor (positivo).
Se o corpo for arremessado verticalmente para cima, o
peso se opõe ao deslocamento e o trabalho é resistente
(negativo).
O trabalho do peso independe da trajetória do corpo.
Situação 4
Também podemos calcular o trabalho através da área do
gráfico (figura 2).
Considere a figura 5. Na figura 5-a, o sistema está em
repouso e a mola não está deformada. A mola, ao ser
alongada, conforme figura 5-b, ou comprimida, conforme
figura 5-c, exerce sobre o corpo uma força elástica que
tende a posicionar o corpo na sua posição inicial,
conforme figura 5-a.
Situação 2
Veja a figura 3. Se uma força resultante F é constante e
não paralela ao deslocamento do bloco, definimos
trabalho de uma força ao produto da projeção da força
resultante, sobre a trajetória de deslocamento, pelo
deslocamento realizado.
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
1
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
Fonte: Os Fundamentos da Física 1 – Mecânica
Ramalho-Nicolau-Toledo, 8ª Ed., Editora Moderna.
Como a força não é constante, no caso de molas, pois
varia com a deformação da mesma, o trabalho da força
elástica será dado por:
k ⋅ x2
τ=±
2
Isto é facilmente dedutível através de um gráfico (figura
6), considerando que a força elástica obedece a lei de
Hooke, sendo dada por F = k ⋅ x e que o trabalho será
dado pela área A do gráfico.
No caso de movimentos circulares: P = M ⋅ .ϖ , ou seja,
potência é o produto do momento, ou torque, pela
velocidade angular.
A unidade de potência no Sistema Internacional de
Unidades (SI) é o Watt (W), sendo permitido o uso
de seus múltiplos e submúltiplos quando
necessário.
1 Watt é a potência capaz de realizar o trabalho de 1 J
em 1 s.
J
N⋅m
= 1⋅
s
s
Fora do SI, duas unidades são de uso comum para
exprimir potência:
Logo: 1 W = 1 ⋅
1 horse-power = 1 hp ≈ 745,7 W
1 cavalo-vapor = 1 cv ≈ 735,5 W
5.1.3. RENDIMENTO MECÂNICO
O trabalho será resistente quando a mola for alongada ou
comprimida e será motor quando ela retornar a sua
posição inicial.
O trabalho da força elástica independe da
trajetória do corpo.
O rendimento, designado pela letra grega η (eta) é dado
pela relação entre a potência útil e a potência total
recebida.
É uma grandeza adimensional que exprime, normalmente
em percentual, o quanto da potência total recebida foi
aproveitada para realizar trabalho útil.
η=
As forças cujo trabalho independe da trajetória são
chamadas de forças conservativas.
O trabalho das forças resistivas depende da forma da
trajetória; são estas, portanto, chamadas de forças
dissipativas.
A unidade de trabalho no Sistema Internacional de
Unidades (SI) é o Joule (J), sendo permitido o uso
de seus múltiplos e submúltiplos quando
necessário.
1 Joule é o trabalho de uma força de 1 N capaz de
provocar um deslocamento de 1 m.
Logo: 1 J = 1 N.m
5.1.2. POTÊNCIA
De todas as formas de potência que existem, vamos nos
ater ao estudo da potência mecânica apenas.
PU
P
A potência perdida na operação (não transformada em
trabalho útil) será dada por Pp = P − PU .
5.1.4. EXERCÍCIOS RESOLVIDOS
1)
Uma motocicleta, partindo do repouso em uma rua
plana e horizontal, atinge 108 km/h em um percurso
de 150 m. Sendo a massa do conjunto moto + piloto
igual a 250 kg e, desprezando qualquer resistência
ao movimento, determine, supondo que o motor
exerça uma força constante e paralela à direção da
velocidade:
a) a potência útil no percurso de 150 m;
b) a potência útil quando o conjunto atingir
108 km/h;
c) o rendimento do conjunto, sabendo-se que a
potência média fornecida pelo motor foi de
34 cv.
Potência é uma grandeza física que, em termos práticos,
exprime o quão rápido uma máquina realiza trabalho.
Solução
Assim, potência é a capacidade de realizar trabalho em
um determinado período de tempo.
τ
Desta forma: P =
∆t
km
m
= 30
h
s
a) Precisamos determinar a aceleração do conjunto.
Vamos aplicar a equação de Torricelli:
V 2 = V02 + 2 ⋅ a ⋅ ∆S ⇒ ( 30 ) 2 = 0 + 2 ⋅ a ⋅ 150
Da equação acima, podemos deduzir outras duas
equações que são também, muito utilizadas.
No caso de movimentos lineares: P = F ⋅ V , ou seja,
potência é o produto da força pela velocidade linear.
Temos um problema de MRUV.
Transformemos as unidades: 108
a = 3 m / s2
O tempo gasto neste percurso é:
V = V0 + a ⋅ t ⇒ 30 = 0 + 3 ⋅ t ⇒
t = 10 s
Sabemos que F = m ⋅ a . Logo:
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
2
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
F = 250 ⋅ 3
Logo: PU =
⇒
F = 750 N
F ⋅ ∆S 750 ⋅ 150
τ
=
=
∆t
∆t
10
A potência (média) será: PU = 11,25 kW ≈ 15 ,3 cv
b) No instante em que se atinge a velocidade de 108
km/h, tem-se a potência instantânea.
Logo:
PU = F ⋅ V = 750 ⋅ 30
c) Sabemos que η =
⇒
PU = 22 ,5 kW ≈ 30 ,6 cv
PU 15 ,3
=
= 0 ,45 ⇒ η = 45%
P
34
“Foram gastos 55% da potência total para vencer os
atritos internos dos sistemas que compõem a moto
mais o atrito com o solo e resistência do ar.”
Resposta: a) 11,25 kW
2)
b) 22,5 kW
c) 45%
A água é retirada de um poço de 18 m de
profundidade com o auxílio de um motor de 5 hp.
Determine o rendimento do motor se 420.000 litros
de água são retirados em 7 horas de operação.
Dados: 1 hp = 0,75 kW, g = 10 m/s² e a densidade da
3
água d = 1 g/cm .
Fonte: Os Fundamentos da Física 1 – Mecânica
Ramalho-Nicolau-Toledo, 8ª Ed., Editora Moderna.
A unidade de energia no Sistema Internacional de
Unidades (SI) é igual à do trabalho, ou seja, Joule
(J), sendo permitido o uso de seus múltiplos e
submúltiplos quando necessário.
5.2.1. ENERGIA CINÉTICA
Consideremos um corpo em movimento retilíneo
uniformemente variado, produzido por uma resultante de
forças que sobre ele atuam.
V 2 = V02 + 2 ⋅ a ⋅ ∆S
⇒
equação de Torricelli
FR = m ⋅ a
De Torricelli, tiramos que: a =
V 2 − V02
2 ⋅ ∆S
V 2 − V02
2 ⋅ ∆S
Trabalhando a equação acima, chegamos a:
V2
V2
FR ⋅ ∆S = m
−m⋅ 0
2
2
Donde tiramos o teorema da energia cinética:
Logo: FR = m ⋅ a = m ⋅
τ = ∆E C
Solução
Primeiro, ajustemos as unidades:
3
d = 1 g/cm = 1 kg/litro
7 horas = 3.600 s
Do teorema acima, concluímos que o trabalho é igual à
variação da energia cinética.
A potência total do motor é 5 hp, mas a potência
utilizada é
posição que este ocupa (energia potencial). Há também,
uma importante relação entre energia e trabalho.
Nosso estudo se concentrará no estudo das energias
relacionadas à Mecânica, pois outras formas de energia
existem, porém, não será objeto desta apostila.
PU =
τ
, onde
∆t
τ será o trabalho
realizado para elevar a quantidade de água retirada
em 7 horas, dado por:
A energia cinética EC de um corpo em movimento é dada
pelo produto de sua massa pela metade da sua
velocidade ao quadrado.
V2
EC = m
2
τ = P ⋅ h = m ⋅ g ⋅ h = d ⋅V ⋅ g ⋅ h
trabalho motor energia cinética aumenta
trabalho resistente energia cinética diminui
m
e P = m⋅g
V
sendo V = volume e h = altura de elevação
5.2.2. ENERGIA POTENCIAL GRAVITACIONAL
pois densidade é d =
Assim: PU =
d ⋅ V ⋅ g ⋅ h 1 ⋅ 4 ,2 ⋅ 10 5 ⋅ 10 ⋅ 18
τ
=
=
∆t
∆t
3 ,6 ⋅ 10 3
A esfera da figura 7 é arremessada verticalmente para
cima, a partir do solo (A), com uma velocidade inicial VA .
Logo: PU = 3 kW ou PU = 3 kW ⋅ 0 ,75 = 4 hp
Portanto, o rendimento será de:
P
4
η = U = = 0 ,8 ⇒ η = 80%
P
5
Resposta: 80%
5.2. ENERGIA
Existe dificuldade em conceituar energia. Com muita
freqüência, associamos energia ao movimento (energia
cinética) de um corpo. Também podemos associar
energia a um corpo em repouso, relacionando-a a
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
3
Polícia Rodoviária Federal
Prof. Dirceu Pereira
Por ter velocidade inicial diferente de zero, tem energia
cinética E C . Ao atingir a altura máxima h B , sua
velocidade VB será zero. Neste ponto, devido ao seu
peso P , se abandonarmos a esfera, esta cairá. Desta
forma, sua força-peso P realizará trabalho, que pelo
teorema da energia cinética de B para A é:
1
τ BA = ∆E C ⇒ P ⋅ ∆h = E CA − E CB ⇒ P ⋅ ∆h = ⋅ m ⋅ ( VA2 − VB2 )
2
Na posição B, VB é zero. Então:
1
⋅ m ⋅ VA2 = E CA
2
Na posição B, a esfera tem potencial de vir a ter energia
cinética devido a força-peso, que realizará trabalho
durante a queda. Assim, em B, a esfera tem uma energia
associada à sua posição, a qual é chamada de energia
potencial gravitacional.
τ BA = P ⋅ ∆h =
Física
Aulas 4 e 5 de 5
apenas transformando-se em suas formas cinética e
potencial.
Desta forma, temos que:
E = EP + E C
De um modo geral, podemos afirmar que a energia
mecânica de um sistema se conserva quando este se
movimenta sob a ação de forças conservativas e,
eventualmente, de outras forças que realizem trabalho
nulo.
Na figura 5-b, na posição A, a mola tem energia potencial
elástica máxima e cinética nula. Ao ser liberada, passa
pelo ponto O (figura 5-a) com energia cinética máxima e
potencial elástica nula. Desprezando os efeitos das
forças dissipativas, o bloco comprimirá a mola (figura 5-c)
fazendo com que esta atinja energia potencial elástica
máxima e cinética nula. E assim, repete-se
indefinidamente, até uma força interrompa o movimento.
Este sistema constitui um oscilador harmônico.
E P = P ⋅ ∆h = m ⋅ g ⋅ ∆h
5.2.3. ENERGIA POTENCIAL ELÁSTICA
Referindo à figura 5-b, ao deslocarmos o bloco de O até
A, provocamos uma deformação na mola e, para tal,
exercemos uma força elástica F = k ⋅ x . Se retirarmos a
força elástica F, o bloco volta à sua posição de repouso
(mola livre).
Neste momento, a força elástica F realiza trabalho que,
pelo teorema da energia cinética de A para O é:
1
τ AO = E CA − E CO = ⋅ m ⋅ ( VA2 − VO2 )
2
Como a velocidade inicial em O é zero, temos:
k ⋅ x2
1
τ AO =
= ⋅ m ⋅ VA2 = E CA
2
2
Logo:
E PE =
k ⋅ x2
2
O gráfico da figura 8 mostra a conservação de energia
para o caso da mola da figura 5.
Portanto, a energia potencial elástica da mola está
associada à sua deformação.
trabalho motor energia potencial elástica diminui
trabalho resistente energia potencial elástica aumenta
5.2.4. CONSERVAÇÃO DA ENERGIA MECÂNICA
Nos processos mecânicos, a energia cinética pode
transformar-se em energia potencial e vice-versa.
A figura 7 nos mostra isso. Na posição A (solo), a esfera
está dotada de velocidade inicial, diferente de zero.
Portanto, na posição A, a esfera tem velocidade máxima
e sua altura inicial é zero. Na medida em que sobe, sofre
a ação da aceleração da gravidade e diminui sua
velocidade, aumentando sua altura do solo. Nas posições
intermediárias, tem energia cinética e potencial. Quanto
mais sobe, menos tem energia cinética e mais tem
energia potencial, proporcionalmente. Na posição B,
altura máxima, sua velocidade é zero, tendo energia
cinética zero e energia potencial máxima.
No caso de haverem forças dissipativas no sistema, parte
da energia total, além de cinética e potencial, poderá
transformar-se em energia térmica, por exemplo, gerando
calor.
isso explica, por exemplo, porque os pneus de um carro
aquecem enquanto este está em movimento.
Em certos casos, outras formas de energia poderão
ocorrer tais como energia luminosa, energia nuclear,
energia elétrica, etc.
5.2.5. EXERCÍCIOS RESOLVIDOS
3)
Um corpo de massa 2 kg é abandonado sobre uma
mola ideal de constante elástica 50 N/m, como
mostra a figura.
Considerando g = 10 m/s² e desprezando as perdas
de energia mecânica, determine:
a) a deformação da mola no instante em que a
velocidade do corpo é máxima;
b) a velocidade máxima do corpo.
Portanto, na ausência de forças dissipativas, a energia
total da esfera, ao longo do trajeto, permanece constante,
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
4
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
c)
a altura do ponto C, hmáx.
Fonte: Os Fundamentos da Física 1 – Mecânica
Ramalho-Nicolau-Toledo, 8ª Ed., Editora Moderna.
Solução
a)
Fonte: Os Fundamentos da Física 1 – Mecânica
Ramalho-Nicolau-Toledo, 8ª Ed., Editora Moderna.
Solução
Inicialmente, o corpo tem energia potencial máxima.
Este começa a cair e, ao tocar a mola, cuja força
elástica é nula, passa a comprimir a mesma,
aumentando gradualmente a força elástica até que
esta se iguale ao peso do corpo. Neste instante, o
corpo atinge sua velocidade máxima.
a)
façamos a equação de equilíbrio no ponto onde
a velocidade do corpo é máxima (deflexão
máxima da mola).
FELAST = P
⇒
k ⋅x = m⋅g
⇒
50 ⋅ x = 2 ⋅ 10
x = 0 ,4 m
b)
E = E PG = m ⋅ g ⋅ h = 60 ⋅ 10 ⋅ 4
E = E C + E PG
E = 2.400 J
⇒
E=
1
⋅ m ⋅V 2 + m ⋅ g ⋅ h
2
Assim, temos que:
1
2.400 = ⋅ 60 ⋅ V 2 + 60 ⋅ 10 ⋅ 0 ,8
2
V = 64
b)
a energia potencial gravitacional do corpo se
transformará em energia cinética e em energia
potencial elástica.
⇒ V =8 m/ s
a partir do ponto B, o indivíduo possui
movimento oblíquo no vácuo. Portanto, sabemos
que nesta posição, a componente vertical da
velocidade é zero e, portanto, a componente
horizontal da velocidade, constante, será a
velocidade considerada.
Do cálculo vetorial, temos VH = V ⋅ cos θ
1
1
2
⋅ m ⋅ VMAX
+ k ⋅ x2
2
2
1
2
2 ⋅ 10 ⋅ ( 0 ,6 + 0 ,4 ) = ⋅ [ 2 ⋅ VMAX + 50 ⋅ ( 0 ,4 ) 2 ]
2
VMAX = 4 m / s
3
=4⋅ 3 m/ s
2
Como a energia total é a mesma, pois não há
perdas, vem:
1
1
E C = ⋅ m ⋅ VH2 = ⋅ 60 ⋅ ( 4 ⋅ 3 ) 2
2
2
E C = 1.440 J
Logo: VH = 8 ⋅ cos 30º = 8 ⋅
Resposta: x = 0,4 m e VMAX = 4 m/s
(Ufla-MG) Um parque aquático tem um toboágua,
conforme mostra a figura abaixo. Um indivíduo de 60
kg desliza pelo toboágua a partir do ponto A, sendo
lançado numa piscina de uma altura de 0,8 m, ponto
B, numa direção que faz ângulo de 30º com a
horizontal.
⇒
Como não existem forças dissipativas, no ponto B, o
indivíduo terá a mesma energia total E. Porém,
agora, esta será composta de energia cinética e
energia potencial gravitacional.
m ⋅ g ⋅(h + x) =
4)
no ponto A, o indivíduo tem energia total igual a
energia potencial gravitacional
c)
sabemos que E = E C + E PG em toda a trajetória
e, portanto:
2400 = 1.440 + m ⋅ g ⋅ hmax
⇒
h max =
960
60 ⋅ 10
h max = 1,6 m
Resposta:
V =8 m/ s
E C = 1.440 J
hmax = 1,6 m
5.3. IMPULSO E QUANTIDADE DE MOVIMENTO
Considerando a atrito desprezível, g = 10 m/s² e
3
, calcule:
2
a velocidade do indivíduo ao deixar o toboágua
no ponto B;
a energia cinética do indivíduo no ponto mais
alto da trajetória, ponto C;
cos 30º =
a)
b)
O produto da força pelo intervalo de tempo em que a
mesma é aplicada constitui o impulso da força. Esta
grandeza está associada ao princípio da conservação da
quantidade de movimento, como logo veremos.
5.3.1. IMPULSO DE UMA FORÇA
O jogador, na figura 9, ao chutar uma bola, transmite uma
determinada força na mesma, durante um certo intervalo
de tempo.
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
5
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
módulo: Q = m ⋅ V
direção: a mesma de V e paralela a esta
sentido: o mesmo de V , pois m é positiva
A unidade de quantidade de movimento no
Sistema Internacional de Unidades (SI) é
quilograma vezes metro por segundo (kg.m/s),
sendo permitido o uso de seus múltiplos e
submúltiplos quando necessário.
5.3.3. TEOREMA DO IMPULSO
Ao produto desta força pelo intervalo de tempo em que
esta foi aplicada, chamamos de impulso de uma força.
Ι = F ⋅ ∆t
O impulso é uma grandeza vetorial e tem:
O impulso da força resultante num intervalo de tempo é
igual à variação da quantidade de movimento do corpo no
mesmo intervalo de tempo.
Ι R = Q 2 − Q 1 = ∆Q
Pelo teorema do impulso, vemos que as unidades de
impulso e quantidade de movimento são equivalentes e
não possuem nomes especiais.
módulo: Ι = F ⋅ ∆t
direção: a mesma de F e paralela a esta
sentido: o mesmo de F , pois ∆t é positivo
A unidade de impulso no Sistema Internacional de
Unidades (SI) é Newton vezes segundo (N.s),
sendo permitido o uso de seus múltiplos e
submúltiplos quando necessário.
Como a força aplicada é constante no intervalo de tempo
considerado, temos o gráfico da figura 10.
N⋅s =
kg ⋅ m
s
5.3.4. CONSERVAÇÃO DA QUANTIDADE DE
MOVIMENTO
Relembrando, da 1ª lei de Newton, um corpo isolado de
forças externas é entendido como:
a) não atuam forças externas; forças internas
podem existir;
b) existem ações externas, mas sua resultante é
nula;
c) existem ações externas, de pouca intensidade,
tal que podem ser desprezadas;
Se o sistema é isolado de forças externas, a resultante
dessas forças é nula e também é nulo seu impulso.
Do teorema do impulso, vem:
ΙR = Q 2 − Q 1 = 0
⇒
Q1 = Q 2
Podemos, então, enunciar o princípio da conservação da
quantidade de movimento:
A partir deste gráfico, temos que a área sob a reta onde F
é constante é numericamente igual ao impulso. Assim:
A=Ι
5.3.2. QUANTIDADE DE MOVIMENTO
Considere um corpo de massa m com velocidade V num
determinado referencial. A quantidade de movimento,
ou momento linear, desse corpo é a grandeza vetorial
dada por:
Q = m⋅V
A quantidade de movimento é uma grandeza vetorial e
tem:
A quantidade de movimento de um sistema de
corpos isolados de forças externas é constante.
Os princípios da conservação de energia e da quantidade
de movimento são independentes, ou seja, a quantidade
de movimento pode permanecer constante ainda que a
energia mecânica não permaneça.
5.3.4. CHOQUES
Uma colisão frontal entre dois corpos que se movem na
mesma reta, antes e depois da colisão, é chamada de
choque frontal ou unidimensional.
Consideremos os corpos A e B, isolados de forças
externas, colidindo sem apresentar deformações
permanentes, conforme mostra a figura 11.
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
6
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
O corpo A colide frontalmente com o corpo B em (a).
Durante um curtíssimo intervalo de tempo em (b), A e B
sofrem deformações elásticas transformando a energia
cinética inicial de A em energia potencial elástica dos
corpos deformados. Quase que instantaneamente, os
corpos restituem sua forma inicial, convertendo a energia
potencial elástica novamente em energia cinética em (c),
considerando que nesse processo não haja dissipação de
energia.
Portanto, se a energia cinética final é igual a energia
cinética inicial, a colisão é chamada de choque
perfeitamente elástico.
Como a quantidade de movimento também se conserva
durante a colisão, temos:
Antes da colisão
Q A = m A ⋅ VA
e
E CA =
1
⋅ m A ⋅ VA2
2
Depois da colisão
Q D = m A ⋅ VA + m B ⋅ VB
E CD
Pelos princípios da conservação de energia e da
quantidade de movimento, temos:
E CA = E CD
⇒
⇒
Como a quantidade de movimento também se conserva
durante a colisão, temos:
Antes da colisão
Q A = m A ⋅ VA
m A ⋅ VA = m A ⋅ VA + m B ⋅ VB
m A ⋅ VA2 = m A ⋅ VA2 + m B ⋅ VB2
“Corpos idênticos em colisões perfeitamente
elásticas e frontais trocam de velocidade”.
Porém, existem choques diferentes do anterior, onde um
corpo A colide com um corpo B muito deformável, por
exemplo, massa de modelar. Após a colisão, o corpo A
se aloja no interior do corpo B, dissipando energia
transformando esta em calor, aumentando a temperatura
dos corpos.
Um exemplo típico é um projétil A projetando-se contra
uma massa deformável B, muito superior a massa
daquele, conforme mostra a figura 12.
Em choques deste tipo, conserva-se a quantidade de
movimento, mas não se conserva a energia cinética,
sendo a final menor que a inicial. A diferença
corresponde a energia térmica liberada.
e
E CA =
1
⋅ m A ⋅ VA2
2
Depois da colisão
Q D = (m A + m B ) ⋅ V
E CD =
1
⋅ (m A ⋅ m B ) ⋅ V 2
2
Pelos princípios da conservação de energia e da
quantidade de movimento, temos:
Q A = QD
1
1
= ⋅ m A ⋅ VA2 + ⋅ m B ⋅ VB2
2
2
Q A = QD
Choques em que os corpos se deformam de tal maneira
que permaneçam unidos após a colisão, são
denominados de choques perfeitamente inelásticos.
E CA > E CD
⇒
⇒
m A ⋅ VA = (m A ⋅ +m B ) ⋅ V
dissipação de energia
Se o choque se situa entre o perfeitamente elástico e o
perfeitamente inelástico, ele é chamado de choque
parcialmente elástico.
Nesse choque, também há conservação da quantidade
de movimento e perda de energia cinética, mas os corpos
se separam após o choque.
5.3.5. COEFICIENTE DE RESTITUIÇÃO
É a razão entre a velocidade relativa de afastamento dos
corpos depois do choque e a velocidade relativa de
aproximação antes do choque.
e=
velocidade relativa de afastamento (depois )
velocidade relativa de aproximação (antes)
Para determinar a variação da energia cinética ocorrida
em um choque, podemos recorrer ao coeficiente de
restituição.
A tabela 1 mostra os valores do coeficiente de restituição
e para os diferentes tipos de choque.
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
7
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
Resolvendo (2) e (3), temos:
Tipos de
choque
perfeitamente
inelástico
parcialmente
elástico
perfeitamente
elástico
Valor de e
Energia
(2)
(3 )
e=0
máxima dissipação
V A( A ) = V D ( B ) − V D ( A )
0<e<1
dissipação parcial
V A( A ) = VD( B )
e=1
conservação da
energia cinética
VD( A ) = 0
Como queríamos demonstrar.
(tabela 1)
5.3.6. EXERCÍCIOS RESOLVIDOS
5)
V A( A ) = V D ( A ) + V D ( B )
Aplicando o princípio da conservação da energia e,
sabendo que não existem forças dissipativas,
concluímos que a altura que a esfera B vai atingir
será a mesma da esfera A no início do movimento,
ou seja, hB = 0 ,5 m .
Um pêndulo, conforme mostrado na figura abaixo,
está inicialmente em repouso, com a esfera A na
posição indicada. As esferas são idênticas e de
massa 1 kg. Ao soltar-se a esfera A, esta irá colidir
com as demais, provocando um choque
perfeitamente elástico. Pede-se:
b)
Pelo princípio da conservação da energia, temos
que:
1
E P ( A ) = E C( B ) ⇒ m ⋅ g ⋅ h = ⋅ m ⋅ V 2
2
1
2
1 ⋅ 10 ⋅ 0 ,5 = ⋅ 1 ⋅ V
⇒ V = 10
2
V ≅ 3 ,16 m / s
Resposta: hB = 0 ,5 m e V = 3 ,16 m / s
a)
b)
provar que a esfera B, após o choque, irá atingir
a mesma altura inicial da esfera A e esta irá ficar
parada;
calcular a velocidade inicial da esfera B.
Considere g = 10 m/s² e despreze qualquer tipo de
força dissipativa.
6)
Um projétil de massa m = 20 g é atirado
horizontalmente com velocidade V0 contra um
pêndulo vertical cuja massa pendular é M = 2 kg e de
fácil penetração. O projétil aloja-se no pêndulo e,
devido ao choque, o conjunto sobe até a altura h =
20 cm. Adote g = 10 m/s² e determine a velocidade
inicial do projétil, bem como a energia dissipada no
fenômeno.
Solução
a)
devemos, em síntese, provar que as esferas A e
B, após a colisão, trocam de velocidade, ou seja,
a esfera B adquire a velocidade de A e viceversa.
Antes da colisão: Q A = m ⋅ V A( A ) + m ⋅ V A( B )
Depois da colisão: QD = m ⋅ VD( A ) + m ⋅ VD( B )
Fonte: Os Fundamentos da Física 1 – Mecânica
Ramalho-Nicolau-Toledo, 8ª Ed., Editora Moderna.
Pelo princípio da conservação da quantidade de
movimento.
Q A = QD
Solução
m ⋅ V A( A ) + m ⋅ V A( B ) = m ⋅ VD( A ) + m ⋅ VD( B )
(1 )
Antes da colisão: V A( B ) = 0
Logo, de (1), temos: V A( A ) = VD( A ) + VD( B )
(2 )
Se o choque é perfeitamente elástico, sabemos que
o coeficiente de restituição é igual a 1.
e=
1=
É um choque perfeitamente inelástico, pois a bala
aloja-se no pêndulo após o choque. Há perda de
energia cinética na penetração da bala, mas a
quantidade de movimento do conjunto bala-pêndulo
permanece constante.
Da conservação de energia, vem:
1
EC = E P ⇒
⋅ (M + m ) ⋅V 2 = (M + m ) ⋅ g ⋅ h
2
Logo :
V = 2 ⋅g ⋅h
(1 )
velocidade relativa de afastamento ( depois )
=1
velocidade relativa de aproximação ( antes )
Da conservação da quantidade de movimento vem:
VD( B ) − VD( A )
Q A = QD
V A( A )
⇒ V A( A ) = VD( B ) − VD( A )
(3 )
⇒
m ⋅ V0 = ( M + m ) ⋅ V
(2 )
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
8
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
Após a colisão, a energia cinética do conjunto se
transforma em energia potencial quando o pêndulo
atinge a altura h.
V0 =
2 + 20 • 10 −3
20 • 10 −3
V0 = 200 m / s
⇒ V0 =
M +m
⋅ 2 ⋅g ⋅h
m
⋅ 2 ⋅ 10 ⋅ 20 • 10 −2
Para determinar a dissipação de energia no
fenômeno, basta calcularmos as energias cinéticas
antes e depois da colisão.
1
1
E C ( A ) = ⋅ m ⋅ V02 = ⋅ 20 • 10 −3 ⋅ 200 2
2
2
E C ( A ) = 400 J
1
1
⋅ ( M + m ) ⋅ V 2 = ⋅ ( 2 + 20 • 10 −3 ) ⋅ 2 2
2
2
=4J
EC( D ) =
EC( D )
Estabelecendo uma
encontrados, temos:
EC( D )
EC( A )
=
relação
1 dina
1 cm 2
Os aparelhos que medem pressão são denominados
manômetros.
Substituindo (1) em (2), temos:
m ⋅ V0 = ( M + m ) ⋅ 2 ⋅ g ⋅ h
1b =
entre
os
valores
4
= 0 ,01 = 1%
400
Este resultado significa que a energia cinética depois
da colisão é apenas 1% da energia cinética inicial;
foram dissipados no fenômeno 99% da energia
cinética inicial, transformada em energia térmica.
UNIDADE 6 – HIDROSTÁTICA
A Hidrostática, termo consagrado pelo uso, estuda os
fluídos (líquidos e gases) em equilíbrio, analisando a
pressão que exercem e a força com que atuam sobre
corpos neles imersos.
Em nosso caso, estudaremos apenas os líquidos, os
quais são considerados, sob condições normais, como
incompressíveis.
6.1. PRESSÃO
A grandeza dada pela relação entre a intensidade da
força F que atua perpendicularmente sobre uma área A é
denominada pressão (p).
F
p=
A
6.2. MASSA ESPECÍFICA E DENSIDADE
Massa específica (µ = mu) de uma substância
homogênea é definida como o quociente da massa m
desta substância e o seu volume V.
m
µ=
V
Densidade (d) de um corpo, homogêneo ou não, é
definido como o quociente entre a massa m deste corpo e
o seu volume V.
m
d=
V
Se um corpo é maciço e homogêneo, sua densidade
coincide com a massa específica do material que o
constitui.
Se por exemplo, tivermos um cubo maciço de aço, cuja
3
massa específica é 7,85 g/cm , sua densidade também
3
será 7,85 g/cm . Porém, se este cubo for oco, sua
densidade será menor que a massa específica, uma vez
que teremos uma massa menor ocupando o mesmo
volume.
Os líquidos, considerados sempre homogêneos, não têm
distinção entre densidade e massa específica.
A unidade de massa específica e densidade no
Sistema Internacional de Unidades (SI) é
3
guilogramas por metro cúbico (kg/m ), sendo
permitido o uso de seus múltiplos e submúltiplos
quando necessário.
6.3. PRESSÃO EM UM LÍQUIDO
Teorema de Stevin
A pressão em um ponto situado à profundidade h no
interior de um líquido em equilíbrio é dada pela pressão
na superfície, exercida pelo ar ( p A ), chamada pressão
atmosférica, somada à pressão exercida pela coluna
líquida situada acima do ponto ( p H ).
p = p A + pH
⇒
p = pA + d ⋅ g ⋅ h
A unidade de pressão no Sistema Internacional de
Unidades (SI) é Pascal (Pa), sendo permitido o uso
de seus múltiplos e submúltiplos quando
necessário.
1 Pa =
1N
1 m2
Eventualmente, fora do SI, é usado o bária (b), cujo plural
é bar.
Na figura 1 acima, um objeto está mergulhado no lago de
uma represa à profundidade h. A superfície da água está
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
9
Polícia Rodoviária Federal
Prof. Dirceu Pereira
Física
Aulas 4 e 5 de 5
sob pressão atmosférica p A , sendo d a densidade da
água e g a aceleração da gravidade.
Do teorema de Stevin, concluímos que todos os pontos
situados na mesma profundidade h, estarão sujeitos a
mesma pressão.
Da mesma, todos os pontos na superfície de um líquido
em equilíbrio estão sujeitos a mesma pressão
atmosférica.
Portanto, dizemos que, em um líquido homogêneo em
equilíbrio, qualquer superfície horizontal é isobárica
(mesma pressão).
Podemos também retirar, do teorema de Stevin, unidades
de pressão consideradas práticas, baseadas na pressão
da coluna líquida.
Tais unidades correspondem às pressões hidrostáticas
que exercem em sua base as colunas de líquido com
alturas equivalentes a unidade considerada.
Por exemplo:
Assim, temos a seguinte conversão para m.c.a.:
O tubo em U está sujeito à pressão atmosférica em
ambos os bocais nas situações (a) e (b). Na situação (a),
o tubo contém água em equilíbrio, estando os pontos A e
B, na mesma superfície horizontal, sujeitos à mesma
pressão. Na situação (b), adicionamos óleo pelo bocal
direito do tubo. No início, devido a forças dinâmicas, há
uma pequena mistura entre óleo e água. Após cessar as
forças dinâmicas, atinge-se o equilíbrio e o óleo, por ter
densidade menor que a água, vai para a parte superior.
Os pontos A e B, posicionados na mesma superfície
horizontal, continuarão sob mesma pressão, ainda que as
alturas sejam diferentes.
1 m.c.a. = 0,0968 atm (atmosferas)
1 m.c.a. = 0,0098 MPa
1 m.c.a. = 0,0980 bária
Para que haja equilíbrio:
p A = pB
centímetros de mercúrio = cmHg (a 0ºC e 9,8 m/s²)
milímetros de mercúrio = mmHg (a 0ºC e 9,8 m/s²)
metros de coluna d’água = m.c.a. (a 20ºC e 9,8 m/s²)
6.4. PRESSÃO ATMOSFÉRICA
Acima de cada ponto da superfície terrestre, podemos
considerar que há uma coluna de ar exercendo pressão.
À esta damos o nome de pressão atmosférica, a qual
varia com a altitude do local. Na medida em que a altitude
aumenta, diminui a pressão atmosférica.
Experiências de Torricelli com o mercúrio determinaram
que a pressão atmosférica, ao nível do mar, era capaz de
sustentar uma coluna de mercúrio de 76 cm de altura.
Assim define-se outra unidade de pressão: a atmosfera.
1 atm = 76 cmHg = 760mmHg, ao nível do mar.
Quando a pressão atmosférica for igual a 1 atm, ela é
denominada de pressão normal.
p atm + d1 ⋅ g ⋅ h1 = p atm + d 2 ⋅ g ⋅ h 2
Logo:
d1 ⋅ h 1 = d 2 ⋅ h 2
6.6. PRINCÍPIO DE PASCAL
“Os acréscimos de pressão sofridos por um ponto de um
líquido em equilíbrio são transmitidos integralmente a
todos os pontos do líquido e das paredes do recipiente
que o contém.”
Como decorrências práticas da aplicação deste princípio,
temos o freio hidráulico de automóveis e a prensa
hidráulica.
Vejamos a prensa hidráulica, esquematizada na figura 3.
p normal = 1 atm
Ao nível do mar, a pressão atmosférica é, em média,
igual à pressão normal.
O manômetro usado para medir a pressão atmosférica é
denominado barômetro.
6.5. EQUILÍBRIO DE LÍQUIDOS IMISCÍVEIS
Quando dois líquidos, que não se misturam (imiscíveis),
são colocados em um mesmo recipiente, eles se dispõem
de modo que o líquido de maior densidade ocupa a parte
de baixo e o de menor densidade, a parte de cima,
obtendo-se uma superfície de separação horizontal
conforme mostra a figura 2.
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
10
Polícia Rodoviária Federal
Física
Aulas 4 e 5 de 5
Prof. Dirceu Pereira
Se aplicarmos ao êmbolo menor, de área A1, uma força
F, o líquido fica sujeito a um acréscimo de pressão. Como
esta se transmite integralmente através do líquido, o
êmbolo maior, de área A2, fica sujeito ao mesmo
acréscimo de pressão.
F1
F
p1 = p 2 ⇒
= 2
A1 A 2
Portanto, as intensidades das forças aplicadas são
diretamente proporcionais às áreas dos êmbolos.
Logo: T2 = Papar = P − E
Inúmeras experiências nos conduzem a:
Todo corpo sólido mergulhado num fluído em
equilíbrio recebe uma força de direção vertical e
sentido de baixo para cima cuja intensidade é igual
ao peso do fluído deslocado.
Logo, a intensidade do empuxo é dada por:
O volume deslocado no recipiente menor passa para o
recipiente maior. Daí, tiramos que:
V = A ⋅h
⇒
V1 = V2
A 1 ⋅ h1 = A 2 ⋅ h 2
E = d⋅ V ⋅g
onde:
d = densidade do fluído
V = volume deslocado (volume do corpo imerso no fluído)
g = aceleração da gravidade
Portanto, numa prensa hidráulica, os deslocamentos
sofridos pelos êmbolos são inversamente proporcionais
às suas áreas.
Assim, o que se ganha em intensidade de força, perde-se
em deslocamento do êmbolo.
6.7. EMPUXO DE UM LÍQUIDO
O empuxo E que um líquido exerce sobre um corpo nele
mergulhado é uma força vertical, de sentido para cima,
que se contrapõe às forças exercidas pelo corpo sobre
ele.
Analisemos o bloco imerso em água na figura 4.
A unidade de empuxo no Sistema Internacional de
Unidades (SI) é Newton (N), sendo permitido o uso
de seus múltiplos e submúltiplos quando
necessário.
6.8. EXERCÍCIOS RESOLVIDOS
1)
O corpo da figura está preso a uma mola nãodeformada e a um fio de peso desprezível. Seu
volume é 20 litros e está totalmente imerso em água.
A constante elástica da mola é 50 N/cm. Na figura
(b), o fio foi cortado e o corpo atingiu o equilíbrio,
deformando a mola de um comprimento x.
Determine x.
(Dados: densidade da água = 1 g/cm³, g = 10 m/s² e
massa do corpo = 8 kg).
Fonte: Os Fundamentos da Física 1 – Mecânica
Ramalho-Nicolau-Toledo, 8ª Ed., Editora Moderna.
Solução
Inicialmente, o bloco suspenso por um fio não está
imerso no líquido e temos que a tração T1 no fio é igual
ao peso P do bloco. Ao mergulharmos o bloco na água,
este atingirá o equilíbrio, podendo ficar total ou
parcialmente imerso. Neste momento, a tração T2 no fio
será menor que o peso do bloco P .
A força que o líquido exerce sobre o bloco (empuxo)
equilibra esta relação.
T2 = P − E
Fazendo as transformações das unidades:
densidade da água = 1 g/cm³ = 1 kg/litro
O empuxo no corpo, nas duas situações, é o mesmo,
pois o corpo permaneceu totalmente imerso.
O empuxo é dado por E = d ⋅ V ⋅ g = 1 ⋅ 20 ⋅ 10
Logo, o empuxo é E = 200 N
O peso do corpo é P = m ⋅ g = 8 ⋅ 10 = 80 N
A força de intensidade T2 costuma ser chamada de
peso aparente.
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
11
Polícia Rodoviária Federal
Prof. Dirceu Pereira
Física
Aulas 4 e 5 de 5
Como o empuxo é maior que o peso, o
corpo tende a subir. Na situação 1, o
fio impede a subida do corpo. Na
situação 2, o fio é cortado e o corpo
sobe, deformando a mola. Depois de a
mola sofrer a deformação x, o
equilíbrio é obtido.
A força Felast que a mola exerce no corpo tem
intensidade:
F +P =E ⇒
F = 120 N
F = E − P = 200 − 80
Pela lei das deformações elásticas do Hooke:
F = k ⋅x
F 120
=
k
50
x=
⇒
⇒
x = 2 ,4 cm
Resposta: x = 2,4 cm
2)
Considere o arranjo da figura. Queremos erguer o
veículo a uma altura de 1,80 m através da prensa
hidráulica. Sabemos que as áreas dos êmbolos são
A1 = 750 cm² e A2 = 300 cm². A massa do veículo é
de 1.000 kg. Determine o curso h2 necessário, o
volume de óleo deslocado e a força necessária no
êmbolo menor. Considere a aceleração da gravidade
g = 10 m/s².
Solução
Para determinar o curso do êmbolo menor, temos do
princípio de Pascal:
A1 ⋅ h1 = A2 ⋅ h2
h2 = 450 cm
⇒
750 ⋅ 180 = 300. ⋅ h2
h2 = 4 ,5 m
⇒
O volume de óleo deslocado é dado por:
V = A1 ⋅ h1 = A2 ⋅ h2
⇒ V = A1 ⋅ h1 = 750 ⋅ 180
⇒ V = 0 ,135 m 3
F
F
A força necessária será: 1 = 2 ⇒
A1
A2
V = 135.000 cm
3
1.000 ⋅ 10
F
=
750
300
⇒
m⋅g
F
=
A1
A2
F = 4.000 N
Resposta: h2 = 4 ,5 m , V = 0 ,135 m 3 , F = 4.000 N
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
12