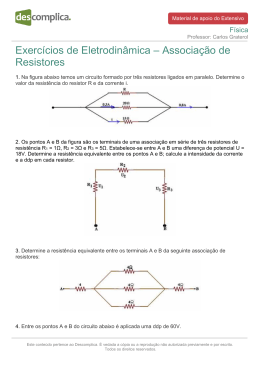
AprovarVI_03.qxp
26/10/2009
17:46
Page 9
Características da Associação em Paralelo
Quando dois ou mais resistores têm seus terminais ligados à mesma diferença
de potencial, de modo a oferecer caminhos separados para corrente.
Física
Professor JULIO CEZAR
Em que Rp é o resistor
equivalente da associação
em paralelo.
Aula 24
Resistores e geradores elétricos
Características da associação em paralelo:
a) A tensão U é a mesma em todos os resistores, pois estão ligados aos
mesmos terminais A e B.
b) A corrente i na associação é igual à soma das correntes em cada resistor:
i = i1 + i2 + i3.
Aplicando-se a 1.ª lei de Ohm a cada um dos resistores, podemos determinar
a resistência do resistor equivalente:
I = i1 + i2 + i3
U
U
U
U
1
1
1
1
–––– = ––– + ––– + ––– → ––– = ––– + ––– + –––
Rp
R1
R2
R3
Rp
R1
R2
R3
O inverso da resistência equivalente é igual à soma dos inversos das
resistências associadas.
No caso de dois resistores associados em paralelo, temos:
1
1
1
1
R1+R2
R1R2
––– = ––– + ––– ⇒ + ––– = ––––––– ⇒ Rp = ––––––––
Rp
R1
R2
Rp
R1R2
R1+R2
Se tivermos n resistores iguais, de resistência R cada um, obteremos.
1
1
1
1
1
n
R1 = R2= R3 = ... e, então, ––– = ––– + ––– + ... + ––– ⇒ ––– = ––– ou
Rp
R
R
R
Rp
R
R
seja: Rp = –––
n
Associação de resistores
Denominam-se resistores todos os aparelhos
elétricos que convertem energia elétrica em energia
térmica (calor), tais como: lâmpada, chuveiro elétrico, ferro de passar roupa, alguns tipos de aquecedores elétricos, etc.
Inúmeras vezes, tem-se necessidade de um valor
de resistência diferente dos valores fornecidos
pelos resistores de que dispomos; outras vezes,
deve atravessar um resistor corrente maior do que
ele normalmente suporta e que o danificaria.
Nesses casos, deve-se fazer uso de uma associação de resistores.
Em qualquer associação de resistores, denomina-se
resistor equivalente o resistor que faria o mesmo
que a associação. Entende-se por resistência da
associação a do resistor equivalente.
Características da associação em série
Vários resistores estão associados em série quando
são ligados um em seguida ao outro, de modo a
serem percorridos pela
mesma corrente.
Aplicação
Dois resistores, de resistências R1 = 6Ω e R2 = 4Ω, são associados em paralelo,
e ao conjunto é aplicada a tensão de 240V. Calcule a intensidade de corrente
e a potência em cada resistor e também na associação.
Solução:
A tensão em cada resistor é também 240V. A lei de Ohm U = R.i aplicada à
R1 fornece:
240 = 6i1 ∴ i1 = 40A
U = R.i pode ser aplicada a R2 é
dá: 240 = 4i2 ∴ i2 = 60A
A intensidade de corrente da
associação é: i = i1 + i2 = 40 +
60 = 100A
Figura 2. a)
Figura 3.
A potência elétrica dissipada em cada resistor associado vale:
Pot1 = R1i2; Pot2 = R2i2; Pot3 = R3i2
Isso equivale dizer que:
Em uma associação de resistores em série, as potências nos resistores são
diretamente proporcionais às respectivas resistências elétricas.
Do ponto de vista do efeito joule, tudo se passa como se houvesse um único
resistor dissipando a potência Pot = Pot1 + Pot2 + Pot3.
Em uma associação de resistores em série, a resistência equivalente é igual
à soma das resistências associadas: RS = R1 + R2 + R3
Se tivermos n resistores iguais, de resistência R cada um, teremos:
R1 = R2 = R3 = ... R, então, Rs = nR
Aplicando a lei de Ohm em cada resistor da figura 3, temos:
U1 = R1i; U2 = R2i;
U3 = R3i;
Portanto podemos concluir que:
A ddp em cada resistor de uma associação em série é diretamente
proporcional à respectiva resistência elétrica.
No resistor equivalente, a ddp vale U = Rsi e, sendo Rs = R1 + R2 + R3,
temos Rsi = R1i + R2i + R3i ⇒ Portanto: U = U1 + U2 + U3
A ddp de uma associação de resistores em série é igual à soma das ddp
nos resistores associados.
P = U.i aplicada a R1 fornece: P1 = 240 x 40 = 9600W
P = U.i aplicada a R2 dá: P2 = 240 x 60 = 14.400W
A potência da associação é: P = 9.600 + 14.400 = 24.000W
Resposta: 40A,9.600W; 60A, 14.400W; 100A, 24.000W
3. ASSOCIÇÃO MISTA DE RESISTORES
As associações mistas de resistores contêm associações em paralelo e
associações em série. Qualquer associação mista pode ser substituída por
um resistor equivalente, que se obtém considerando-se que cada associação
parcial (série ou paralelo) equivale a apenas um resistor.
Para determinar a resistência equivalente em uma associação mista, colocam-se, de início, letras em nós e terminais da associação. Nós são os
pontos em que a corrente se divide; terminais, os pontos entre os quais se
quer determinar a resistência equivalente.
Cuidado: durante o processo, não podem desaparecer os terminais da
associação.
Aplicação
Dois resistores, de resistências R1 = 7Ω e R2 = 3Ω, são associados em
série. A intensidade de corrente da associação vale 10A. Calcule a intensidade de corrente, a tensão e a potência em cada resistor.
Gerador elétrico e força eletromotriz
Gerador elétrico é todo elemento de circuito que transforma em energia
elétrica outra forma de energia.
Solução:
A intensidade de corrente em
cada resistor é também 10A.
A lei de Ohm U = R . i é aplicada à resistência R1 e fornece: U1 = 7 x 10 = 70V
A mesma lei aplicada a R2 dá: U2 = 3 x 10 = 30V
A expressão P = U.i é aplicada a R1 e fornece: P1 = 70 x 10 = 700W
Quando P = U.i é aplicada a R2, temos:
P2 = 30 x 10 = 300W
2. ASSOCIAÇÃO DE RESISTORES EM PARALELO
Todo gerador elétrico é constituído de condutores e, portanto, possui uma
resistência elétrica. Ela é denominada resistência interna de gerador e é
indicada por r.
Quando um gerador não alimenta nenhum circuito externo, dizemos que ele
está em aberto. Isso significa que a corrente elétrica que atravessa o gerador
é nula, mas, mesmo assim, existe uma tensão elétrica entre seus polos. Essa
tensão é indicada pela letra E e é denominada força eletromotriz (abreviadamente, fem). Portanto a força eletromotriz é a tensão elétrica entre os polos
de um gerador em circuito aberto, ou seja, quando i= 0.
O gerador é representado, nos circuitos elétricos, pelo símbolo indicado na
figura1, no qual aparecem os valores de E e r, duas constantes do gerador.
Ligando-se um voltímetro ideal aos polos de um gerador, este não será
percorrido por corrente elétrica; portanto o voltímetro marcará a força
eletromotriz E do gerador (fig.2).
Figura 1. Símbolo de um
gerador
9