~ercíc~os
~11!;:
Propostos
.,
, "
-
".
~tl) Quatro
resistores
'RI
= IK5, R2 = 4K7,
são ligadó!1 em série.
Sabendo-se
determinar:
.
que
.,-
R3 = 470 fie
R4
a ;'tensão em R3 é
~
= 2K2
94OrnV.
~-- ~---
"
~.
".
a) Res~stência equivalente...~'-o.
b) Tensão aplicada na' associação"
c) Potência
dissipada
gerador.
nos
resistores e a potência elétrica
do,
,
,..
i
~) No circuito, determinar a resistência total do
potenciômetro
;. (linear),'~'
sabendo-se que o cursor se encontra na metade
s~u curso
total,
que, a corrente",po ,.circuito vale
dI;)
IA e que
a
."
tensão
pada?
na lâmpada
vale
II0V. Qual
a potência
dissipada
na lâ~
E nopotenciômetro?
~'
~
.~
{
",",
",,"
(c""
~
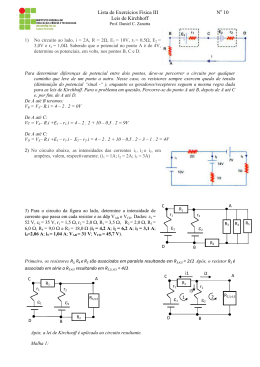
3) No circuito,
que limite deve ser imposto a Rv para que b fusi
vel não queime?
"~'c'
2°L~~'
F: O,OIA
20011.
4) Três .resistore~ RI' R2 e R3 em série dão uma resistência
tal de 3500g. Se R3 é duas vezes R2 e R2 é d~as vezes
quais os valores das resistências?
5) Dois resístores Rl e R2 ligados em série dissipam
tQ
RI,
respectiv~
mente 120mW e 80mW, quando a associação é ligada a uma
de 20V. Quais os valores das resistências?
fonte
6) Dois resistores; Rl ecR2 ligados em série são ligados a
uma
fonte de 40V. Sabendo-se que a potência elétrica do
gerador
é lOW, e que a potência dissipada em RI é 4W, quais os
valQ
res de RI e R2?
.1
Exercícios
Propostos
j
1) Quatro-resistores',
RI"""
são.,.ligados
en~ paralelo.
10OmA, determinar:
2)
lK5,
RZ =4K7,
Sabendo-se
RJ = 470,,-e
que
R,f"='.
a corrente
é
em RJ
a)
Resistência
b)
Corrente
em todos
c)
Potência
dissipada em todos os resistores e no equivalente
Dois
equIvalente
os
resistores
e a
fornecida
pela
fonte
resistores são ligados em paralelo,'sendo um o dobro
outro.
Aplicando-se
uma tensão de ZOV na associação,
do
verifi
ca-se.que .0 de menor valor é percorrido por uma corr.ente
'O,IA. Quais o~~ vaioies,das resistências?.Qual o valor da
tência
dissipada em 'cada resistor?,""
J)
ZKZ .:'
de
P.9.
Três resistores,~RI, RZ e RJ são l-t.gadqs em para,lelo. Saben
do-se que a potência em RJ é duas ~ezes a potência dissipada
RZ, que a potência dissipada em RZ é três vezes a
em RI, e que a""potência
elétricado gerador ele 12V
Quais os valores de RI,
R2 e R3?
dissipada
é.
1, 2W.
4) Quantos resisto;es"de l20n
ra dar uma resistência
5) Determine
Rl tal que
devem ser"ligados em paralolo,
equivalente
l'I'
d~ 30Q?
JOOQ
RE seja
RE=300.o.r
E
6) Determinar
e
-
R2
no circuito
18mA
E
-
16m/.
R'=6K
'~
7) Determinar
'
E,' Rl e, RJ
]
R,o3<
no circUi,to
;.
,
J
" \3m~
R2
= 2K
,,
.)
8) Dois resistores Rl e R2,'quando ligados em paraleJllo,
dhlij)t'1!\
240mW,
consumindo
uma corrente
~e 20mA.
Sabend~-se
tência dissipa'daem Rl é 96mW, ~alcular os va!l!oree
4.3 Div~5°X: d}i!-
T~n5ão - Divisor
de
total ~aplidkda na asso;iaçã~
ligados (1m
s~ dividia
pelo.
em cada rl3lll:!..t
da associação. Padem:>s
escrever a t§nsão
ção da tensão
"
d.. l(1 .. "11
Corr,ente
Vimos que" quando resisto~es são
tensão
QU8'
.
,JfU 111,
r.MI.I~'"
r.n 11111 'II\n
total.
Na figura 4.3, temos que: UQ
=
Rl.IT,e
U2.
1t2.III'
""Idl
",,'
IT
c,=
~..'E~<
Rl'+R2.
RI.E
UI = RI+R2
R2.E'
U2=
J
Q:lu.,
I
tJ
4.3
i":'S;~
e
'..!:r-
Figura
..~':' .' ,T:i
~)['W""
,L hportanto!#f
I
RI+R2
o',.
.. 1
1 ..I
Exercícios Propostos
11) Determinar a resistência equivalente .em~cada caso entre
pontos A e B
a)
~I
IOK
IOK
t
IOK
IOK
os
'.
B
..>
2K
b)
..' , ;.
2K2K
.
B
2K
c)
4OIl
20Il
A
,':~
d)
50Il
40Il
ç
1 130Il
A
!
20Il
UIOIl
I
mn
08
/
e)
Iq.n..
8-
r)
IK
A
i
O'"
2K
B
20Il
g)
IOIl
I
2) Determinar
,
B
o valor de ,R no circuito.
,
o,
R
-
ImA
3)
Determinar o valor de UT e IT no circuito.
3K
12K
fUT
6K
c:=I
2K
0.-,,"
,4)Determinar ~ intensidade da correpte ',em"'todos
.os resistores.
LI
.!!-
!4
10IL
~
10IL
.';0.0.
.,.AV
20.0:
16
,
.~
5) Quer-se' obter
resistores
uma resistência
de 1Q. Como devem
c.
, "".~
de ,,3,5Q COm o menor
ser ligados
de
número
en,tre,.
si? 'YFaça
"
',."
"
b.
"',
ef:
-
quema.
. "I
6) No circuito, determine qual
o valor
de R para
i dev,es~r
'
.
,
a potência
elétr ica
que
do ge);'ador se j.a"50mW.
R
.'
'v',
,
7) Determinar
R para que
I
= 2,25mA
..',
5K
250IL
/
12V
8)
Determinar R para que a lámpada funcione"" dentro
racterísticas.
de suas
ct
>..,
..
"
.~.
60!l.
"
.',
"
'~'"
!
\"
L:6V/IOOmA
I
.;
9) Dois resistores RI
e
R2
em paralelo dissipam
um total
de
360mW. Sabendo-se que a fonte fornece 30mA e que a
potência
dissipada em RI é 72mW, quais os valores de RI e R2?
10)Determinar RI no circuito para que a resistência
'"
entre A e B seja '3KI1.
equivalente
::I]4K
- ..---.-..
11)No circui te, a fonte fornece urnapotência de 2W. Determinar:
a) valor de RI e R2
b) Corrente em RI
LJ'
fm,
12)Determinar RI e R2 no circuito.
--O.IA
20V
;..
" . ,',.
.;_.
R2
I)"
13) Determinar
I no circuito.c
~I
IOK
5K
14) Determinar
Rx para que I
=
4mA.
..L12V
4K
Rx
,
15) Determinar
Rx para que I
=
8mA.
IK
l~
16) Determinar Rx para que
"-é';
IT = ~5mA
~
... """"',;;::.
'~"';"";:;:"'.;L"'.';"
,
13) Determinar
r no circuito.
:,
~I
15K
IOK
!
5K
D
'14)
Determinar Rx para quer
=
4mA.
l12V
Rx
4K
>;
",\
15)
DeterminarRx para que r = 8mA.
-
20mA
IK
l~
16)
DeterminarRx para que rT
=
lSmA
.,--,'
. <.
"..,;
.(;.-'"
",,""""",.
~,'
,~-
lI.-
..
" ~,?",.,
-->
<.,,-" . t,
."
'I",-j
3V
300fi
R~
17)
No
circuito, qual o menor valo~ que o reostato pode assumir,
.om que o fusível
queime?
D.SA
8fi
~,
L
j-
80fi
I fi) No circuito,os fusíveisapresentammesma resist-ência Qual
e máxima corrente qUe pode passar pela lâmpada, sem que haja
queima de qualquer fusível?
Obs.: Os fusíveis têm mesma resistência.
--IA
2A
I
llIL
3A
--
/T
I
4A
I
ÁÀL
",.",{o'l.o"
Propostos
,
1,) "ftlll.
f'ormar
para,
triâ.-ngu19',
A
"
20.0.
10.0.
c
B
.,1
....
'",,-,
..
.""",t
~~""'r~"'r';{""
'"
~""""".
;2'r'Tràns"formar'ÚJara"'estr\ha.
A
"
c
3)
Determinar
a)
A
B
I'"
a resistência
equivalente
entre
;',
A e C
.
,".
60fi
c
b)
'
j,
B
60.0.
;'.~~"<
,':~
n~
10fi
A
10.0.
li!I,1
o
30.0.
c
60.0.
10.0.
,I
F
II
4)
Dete'rminar
todas
as
correntes
do
circuito
e a potência
ca do get-ador.
'
elétr:1II
-
I!'
1i
;
"
60V
:<~O.!l" .
"
-15
,("'"
'li"
30.0.
..rJl'io.
no
5) No circuito, determinar o valor da corrente
,
ampe'ríiÍ1etro
,
'.
"
,
~
-
RI
= 101<
R4
=
= SOl<
RiA = 201<
R2
301<
R3
=
R5
= 20
-
151<
" . !' . 'w"
I<
20V
'.
Solução
. Item
dos Exercícios
"
Propostos'...
4.1
1) a) RE = 8,87KI<
b) UT = 17.74V
P2 = 18,8mW,
c) PI = 6mW,
PE
2) RT = 220\2
.3) RVmin
PDL = 1l0W;
P4
=.8,8mW,
PDp = 1l0W
= 8001<
4) RI = 5001<
5) R I =
P3 ""=1,88mW,
=. 35,,48mW
I, 2K
R2 = 10001<
e
6) ~l = 641<
R2
= 8001<
R2
= 961<
R3 = 20001<
Item 4.2
1) a) RE = 2891<
b) II = 31,33mA,
12
=' 10mA,
c) PI = 1,4 7W"
P2
=' 0,47W,
14 = 21,36mA
13 = 100mA,
P4 = lW.
P'3 = 4,7W,
PE = 7,64W
-i
. ,
2) RI = 2001<
R2
'J) RI
R2 = 400Q,
= 4001<,
PI = 2W,
= iW':'"
pz
"
.. I200Q,
;
i
R3 = 200"Q
r.c',:
,--
"
1\
..
.IJIOOt.
-"
-
.
i
4} 4 resistores
S}
= 829,412
RI
6) E = 24V
R2
'" 4K.
,;.
7) RI = 12Kn
R3 = 4KO
8) RI = I,SK
R2
'E = I2V
;; lK
Item 4.4
1) a) 3, 7SKO
f) 4K
b)
2)
R =
c)
SOOS'!
d) 600
60S'!
1T
= UmA
13
=
16
=
12
= O,OSA
6) R = 4000
=
1 OK li
8) R = 600
RZ
,
9 )..RI- '" 2K!L.
'" 5000
10) RI = 6KII
11)
a) RI'" 2S00,
12)
RI
13)
I = O, 6mA
14)
Rx
=
IS)
Rx
'" I,SKII
16)
Rx
=
= 8011,
17) RVmin
12KII
60011
'" 200
18) ILmax = 4A
",;li-
li
3K O
4) 11 = 17 = O,IA,
R
10
g) 60
3) UT = 41V
7)
e)
RZ
'" lK li
RZ = IS00
b) 11 = 80mA
14 = IS .. O,O2"A
,..
1."!tI " !j
II
~I\I'
, 'ffi
II ,,)
- .lto,60
" fJO
ItJ\" H 13,3
RAC = 1101<
RE "' 12,51<
n
I2 "' IA
.&) '1 .. 11\
"li - .a40W
li) I . 'IBmA
b)RAB
:~, ~,.
-
RBC = 55»
Rc = 6,25 Q'; . ~
= 48,1
13 = O
'»'.,
14 = 3A '.
, ~.,
15 ="lA.
'.::,?"