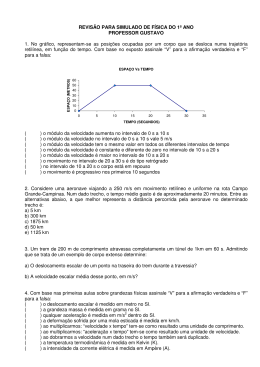
MINI DESAFIO - SIMULADO FUVEST DO OBJETIVO
O Gráfico abaixo descreve a velocidade escalar de um móvel em função do tempo.
Sejam d a distância que ele percorre no trecho em movimento uniforme e a a aceleração do móvel no trecho
retardado.
Determine o menor valor possível para o tempo total T de duração do processo, em função de d e a.
Resolução:
T  t1  t 2 
d v

v a
Queremos determinar o valor mínimo da expressão T 
d v
 , onde d e a são constantes dadas e o parâmetro
v a
v é variável.
Da Matemática, sabemos que, dados dois números X e Y, a média aritmética entre eles é sempre maior ou igual
á média geométrica entre eles, ou seja:
XY
 XY
2
XY

onde a igualdade entre as médias 
 X  Y  só ocorrerá apenas no caso em que tivermos X = Y.
 2

Assim, tomando X e Y como sendo respectivamente
XY
 XY
2

d v

v a 
2
d v


v a
d v

v a 
2
v
d
e
, podemos escrever:
a
v
d
a

d v
d
 2
v a
a
Assim, do resultado obtido acima, concluímos que o valor mínimo da expressão T 
Esse valor mínimo é atingido apenas no caso X = Y, ou seja,
da velocidade V para a qual a expressão T 
d v
d
 vale 2
.
a
v a
v
d
= , o que implica v  a  d . Esse é o valor
a
v
d v
 atinge seu valor mínimo.
v a
A título de curiosidade, nessa condição de Tmin (ou seja, v  a  d ) o quociente entre os tempos t1 e t2 vale:
t1 d / v d  a
da
da




1
2
2
t2 v / a
da
v
( da)
Assim, na condição de Tmin, teremos t1 = t2.