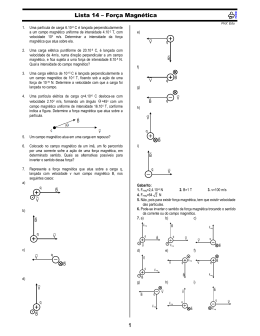
Força Magnética
1. (Espcex (Aman) 2013) Partículas com grande velocidade, provenientes do espaço, atingem
todos os dias o nosso planeta e algumas delas interagem com o campo magnético terrestre.
Considere que duas partículas A e B, com cargas elétricas QA  0 e QB  0, atingem a Terra
em um mesmo ponto com velocidades, VA  VB , perpendiculares ao vetor campo magnético
local. Na situação exposta, podemos afirmar que
a) a direção da velocidade das partículas A e B não irá se alterar.
b) a força magnética sobre A terá sentido contrário à força magnética sobre B.
c) a força magnética que atuará em cada partícula terá sentido contrário ao do seu respectivo
vetor velocidade.
d) a força magnética que atuará em cada partícula terá o mesmo sentido do vetor campo
magnético local.
e) a direção da velocidade das partículas A e B é a mesma do seu respectivo vetor força
magnética.
2. (Unesp 2013) Um feixe é formado por íons de massa m1 e íons de massa m2, com cargas
elétricas q1 e q2, respectivamente, de mesmo módulo e de sinais opostos. O feixe penetra com
velocidade V, por uma fenda F, em uma região onde atua um campo magnético uniforme B,
cujas linhas de campo emergem na vertical perpendicularmente ao plano que contém a figura e
com sentido para fora. Depois de atravessarem a região por trajetórias tracejadas circulares de
raios R1 e R2  2  R1, desviados pelas forças magnéticas que atuam sobre eles, os íons de
massa m1 atingem a chapa fotográfica C1 e os de massa m2 a chapa C2.
Considere que a intensidade da força magnética que atua sobre uma partícula de carga q,
movendo-se com velocidade v, perpendicularmente a um campo magnético uniforme de
módulo B, é dada por FMAG  q  v  B.
Indique e justifique sobre qual chapa, C1 ou C2, incidiram os íons de carga positiva e os de
carga negativa.
m
Calcule a relação 1 entre as massas desses íons.
m2
www.nsaulasparticulares.com.br
Página 1 de 18
3. (Fuvest 2013) Um equipamento, como o esquematizado na figura abaixo, foi utilizado por
J.J.Thomson, no final do século XIX, para o estudo de raios catódicos em vácuo. Um feixe fino
de elétrons (cada elétron tem massa m e carga e) com velocidade de módulo v0, na direção
horizontal x, atravessa a região entre um par de placas paralelas, horizontais, de comprimento
L. Entre as placas, há um campo elétrico de módulo constante E na direção vertical y. Após
saírem da região entre as placas, os elétrons descrevem uma trajetória retilínea até a tela
fluorescente T.
Determine
a) o módulo a da aceleração dos elétrons enquanto estão entre as placas;
b) o intervalo de tempo Δt que os elétrons permanecem entre as placas;
c) o desvio Δy na trajetória dos elétrons, na direção vertical, ao final de seu movimento entre
as placas;
d) a componente vertical vy da velocidade dos elétrons ao saírem da região entre as placas.
Note e adote: Ignore os efeitos de borda no campo elétrico; Ignore efeitos gravitacionais.
4. (Ime 2013)
A figura acima apresenta uma partícula com velocidade v, carga q e massa m penetrando
perpendicularmente em um ambiente submetido a um campo magnético B. Um anteparo está a
uma distância d do centro do arco de raio r correspondente à trajetória da partícula. O tempo,
em segundos, necessário para que a partícula venha a se chocar com o anteparo é:
2
r.
Dados: v = 10 m/s; B = 0,5 T; q  10μc; m  10  1020 kg; d 
2
a) 40 π  1015
b) 20 π  1015
c) 10 π  1015
d) 5 π  1015
e) 2,5 π  1015
www.nsaulasparticulares.com.br
Página 2 de 18
5. (Ita 2012) Considere dois fios paralelos, muito longos e finos, dispostos horizontalmente
conforme mostra a figura. O fio de cima pesa 0,080 N/m, é percorrido por uma corrente I 1 = 20
A e se encontra dependurado por dois cabos. O fio de baixo encontra-se preso e é percorrido
por uma corrente I2=40 A, em sentido oposto. Para qual distância r indicada na figura, a tensão
T nos cabos será nula?
6. (Unifesp 2012) Uma mola de massa desprezível presa ao teto de uma sala, tem sua outra
extremidade atada ao centro de uma barra metálica homogênea e na horizontal, com 50 cm de
comprimento e 500 g de massa. A barra metálica, que pode movimentar-se num plano vertical,
apresenta resistência ôhmica de 5  e está ligada por fios condutores de massas desprezíveis
a um gerador G de corrente contínua, de resistência ôhmica interna de 5  , apoiado sobre
uma mesa horizontal. O sistema barra-mola está em um plano perpendicular a um campo
magnético B horizontal, cujas linhas de campo penetram nesse plano, conforme mostra a
figura.
Determine:
a) a força eletromotriz, em volts, produzida pelo gerador e a potência elétrica dissipada pela
barra metálica, em watts.
b) a deformação, em metros, sofrida pela mola para manter o sistema barra-mola em equilíbrio
mecânico. Suponha que os fios elétricos não fiquem sujeitos a tensão mecânica, isto é,
esticados.
7. (Ucs 2012) Dentro do tubo de imagem de um televisor, a corrente elétrica, numa bobina,
aplica sobre um elétron passante um campo magnético de 5  104 T, de direção perpendicular
à direção da velocidade do elétron, o qual recebe uma força magnética de 1 1014 N. Qual o
módulo da velocidade desse elétron? (Considere o módulo da carga do elétron como
1,6  1019 C. )
a) 3,34  103 m s
b) 1,60  105 m s
c) 7,60  106 m s
d) 4,33  107 m s
e) 1,25  108 m s
www.nsaulasparticulares.com.br
Página 3 de 18
8. (Espcex (Aman) 2012) Sob a ação exclusiva de um campo magnético uniforme de
intensidade 0,4 T, um próton descreve um movimento circular uniforme de raio 10 mm em um
plano perpendicular à direção deste campo. A razão entre a sua massa e a sua carga é de
108 kg C. A velocidade com que o próton descreve este movimento é de:
a) 4  105 m s
b) 2  105 m s
c) 8  104 m s
d) 6  104 m s
e) 5  103 m s
9. (Upe 2011) Um condutor retilíneo de comprimento l percorrido por uma corrente elétrica i é
imerso em um campo magnético uniforme B. Na figura a seguir, estão disponibilizadas as
seguintes situações I, II, III, IV e V.
Nessas condições, o conjunto que melhor representa o sentido da força magnética que atua
sobre o condutor nos itens I, II, III, IV e V, respectivamente, é
a)
b)
c)
d)
e)
www.nsaulasparticulares.com.br
Página 4 de 18
10. (Ufsc 2011) A figura abaixo mostra quatro fios, 1, 2, 3 e 4, percorridos por correntes de
mesmo módulo, colocados nos vértices de um quadrado, perpendicularmente ao plano da
página. Os fios 1, 2 e 3 têm correntes saindo da página e o fio 4 tem uma corrente entrando na
página.
Com base na figura, assinale a(s) proposição(ões) correta(s).
01) O campo magnético resultante que atua no fio 4 aponta para o leste.
02) A força magnética resultante sobre o fio 4 aponta para o sudeste.
04) Os fios 1 e 3 repelem-se mutuamente.
08) A força magnética que o fio 2 exerce no fio 3 é maior do que a força magnética que o fio 1
exerce no fio 3.
16) O campo magnético resultante que atua no fio 2 aponta para o sudoeste.
32) O campo magnético resultante no centro do quadrado aponta para o leste.
11. (Ufu 2011) Com o crescimento populacional e, consequentemente, urbano, torna-se
necessário o desenvolvimento de novas tecnologias que, além de facilitarem a vida das
pessoas, economizem energia e preservem o meio ambiente. Exemplos de dispositivos com
tais características são os fotocensores, isto é, censores que são acionados através da
incidência de luz.
O princípio básico desses equipamentos é o efeito fotoelétrico, ilustrado na figura abaixo.
Com base nos dados R1 = 1  , R2 = 2  e V = 1 V, responda:
Nos pontos A e B, estão conectados dois fios paralelos entre si que são longos o suficiente
para que os efeitos de borda não sejam levados em conta. As resistências R 1 e R2,
desenhadas na figura acima, representam a resistência intrínseca aos materiais que
constituem os fios, os quais estão separados por uma distância de 10 cm. Responda qual é o
módulo da força magnética por unidade de comprimento entre os fios e se a força será atrativa
ou repulsiva.
www.nsaulasparticulares.com.br
Página 5 de 18
12. (Ufpe 2011) O circuito elétrico plano, mostrado a seguir, possui uma bateria de força
eletromotriz   48 V e resistência interna r  1  (não aparece na figura) ligada a resistores
de resistências R  9  e r  1  (que está na figura). O trecho retilíneo ab do circuito possui
comprimento de 50 cm. No plano do circuito, existe um campo magnético uniforme, de modulo
B = 2,5 T e direção fazendo um ângulo de 37º com a direção do trecho ab. Qual o modulo da
forca magnética que age no trecho ab, em N?
13. (G1 - cftmg 2011) Em uma região de campo magnético uniforme B, uma partícula de
massa m e carga elétrica positiva q, penetra nesse campo com velocidade v,
perpendicularmente a B, conforme figura seguinte.
O vetor forca magnética, que atua sobre a partícula no ponto P, está melhor representado em
a)
b)
c)
d)
14. (Ufpe 2010) Três condutores A, B, e C, longos e paralelos, são fixados como mostra a
figura e percorridos pelas correntes IA, IB, IC, que têm os sentidos indicados pelas setas.
A força magnética resultante que atua sobre o condutor B está dirigida
( ) da esquerda para a direita, no plano da figura.
( ) de baixo para cima, no plano da figura.
( ) de fora para dentro do plano da figura.
( ) da direita para a esquerda, no plano da figura.
( ) de dentro para fora do plano da figura.
www.nsaulasparticulares.com.br
Página 6 de 18
15. (Unesp 2009) Parte de uma espira condutora está imersa em um campo magnético
constante e uniforme, perpendicular ao plano que a contém. Uma das extremidades de uma
mola de constante elástica k  2,5 N / m está presa a um apoio externo isolado e a outra a um
lado dessa espira, que mede 10 cm de comprimento.
Inicialmente não há corrente na espira e a mola não está distendida nem comprimida. Quando
uma corrente elétrica de intensidade i = 0,50 A percorre a espira, no sentido horário, ela se
move e desloca de 1,0 cm a extremidade móvel da mola para a direita. Determine o módulo e o
sentido do campo magnético.
16. (Fuvest 2005) Assim como ocorre em tubos de TV, um feixe de elétrons move-se em
direção ao ponto central O de uma tela, com velocidade constante. A trajetória dos elétrons é
modificada por um campo magnético vertical B, na direção perpendicular à trajetória do feixe,
cuja intensidade varia em função do tempo t como indicado no gráfico.
Devido a esse campo, os elétrons incidem na tela, deixando um traço representado por uma
das figuras a seguir. A figura que pode representar o padrão visível na tela é:
17. (Pucmg 2004) Uma partícula carregada com uma carga positiva está numa região onde
existe um campo magnético E . Assinale a afirmativa correta.
a) Se a partícula estiver em movimento na direção de E , atuará sobre ela uma força devido ao
campo magnético, proporcional ao módulo de E .
b) Se a partícula estiver inicialmente em repouso, ela será posta em movimento pela ação da
força do campo magnético e sua trajetória será um espiral.
c) Em qualquer circunstância, atuará sobre a partícula uma força proporcional ao módulo de E
e perpendicular à direção do campo.
d) Se a partícula estiver em repouso, nenhuma força devido ao campo magnético E agirá
sobre ela.
www.nsaulasparticulares.com.br
Página 7 de 18
18. (Mackenzie 1998) Um corpúsculo eletrizado penetra num campo magnético uniforme com
velocidade de direção perpendicular às linhas de indução desse campo. Com relação a esse
fato, afirmamos que:
I. A quantidade de movimento do corpúsculo não irá variar em módulo.
II. O módulo da velocidade do corpúsculo irá variar.
III. O corpúsculo passará a descrever trajetória retilínea.
IV. O corpúsculo passará a descrever trajetória circular.
São corretas as afirmações:
a) I e II
b) I e III
c) I e IV
d) II e IV
e) III e IV
19. (Mackenzie 1998) Em trabalhos de Física Nuclear, são utilizadas diversas partículas
elementares com inúmeras finalidades. Duas destas partículas são:
- partícula alfa ( q  3,2  1019 C e m  6,7  1027 kg )
- partícula beta ( q  1,6  1019 C e m  9,1 1031kg )
Quando uma partícula alfa e uma partícula beta são disparadas separadamente com a mesma
velocidade, perpendicularmente às linhas de indução de um mesmo campo magnético
uniforme, a figura que melhor representa as trajetórias distintas dessas partículas é:
www.nsaulasparticulares.com.br
Página 8 de 18
20. (Mackenzie 1996) O condutor AB da figura a seguir está imerso numa região onde atua um
campo de indução magnética B de intensidade 0,5 T, perpendicular ao plano desta folha e
orientado para o leitor. O condutor situado no plano desta folha é percorrido por uma corrente i
= 2A. A intensidade da força magnética que atua sobre o condutor é:
a) 5 N.
b) 4 N.
c) 2 N.
d) 1 N.
e) zero.
21. (Mackenzie 1996) Um pósitron ( q / m  1,75  1011C / kg ) e um elétron
( q / m  1,75  1011C / kg ) penetram simultaneamente pelos pontos m e n, numa região onde
existe um campo de indução magnética uniforme e de intensidade 4,0  102 T .
A penetração das partículas ocorre perpendicularmente às linhas de indução, conforme a
ilustração a seguir, e se chocam no ponto P. Desprezando os efeitos relativísticos, a velocidade
relativa do pósitron em relação ao elétron, no instante do choque é:
a) 5,6  107 m / s .
b) 4,2  107 m / s
c) 3,5  107 m / s .
d) 2,8  107 m / s .
e) 1,4  107 m / s .
www.nsaulasparticulares.com.br
Página 9 de 18
Gabarito:
Resposta da questão 1:
[B]
De acordo com o físico Hendrick Antoon Lorentz (1853-1920), toda carga elétrica lançada com
certa velocidade V em direção a um campo magnético B , fica sujeita à ação de uma força
magnética F , se a direção do vetor velocidade V não for paralela à direção do vetor campo
magnético B .
Caso a carga elétrica seja positiva, utilizamos a regra da mão direita para determinar a
orientação dos vetores:
Caso a carga elétrica seja negativa, utilizamos a regra da mão esquerda para determinar a
orientação dos vetores:
Analisando as alternativas:
[A] Falsa. Como as partículas ficam sujeitas a atuação da força magnética devido a sua
velocidade ser perpendicular ao campo magnético, haverá alteração da direção de suas
velocidades.
[B] Verdadeira. Analisando as regras da mão direita e esquerda, verificamos que se uma
partícula é positiva e outra é negativa, as forças que atuam em cada uma das partículas
terão sentidos opostos.
[C] Falsa. Analisando as regras da mão direita e esquerda, verificamos que a força magnética é
perpendicular ao vetor velocidade.
www.nsaulasparticulares.com.br
Página 10 de 18
[D] Falsa. Analisando as regras da mão direita e esquerda, verificamos que a força magnética é
perpendicular ao vetor campo magnético.
[E] Falsa. Analisando as regras da mão direita e esquerda, verificamos que a força magnética é
perpendicular ao vetor velocidade.
Resposta da questão 2:
Pela regra da mão esquerda, íons de carga positiva sofrem, inicialmente, forma magnética
para a direita, atingindo a placa C1; os íons de carga negativa sofrem, inicialmente, força
magnética para a esquerda, atingindo a placa C 2.
A força magnética age como resultante centrípeta:
FMAG  Fcent

m1 v
R1 
| q1 | B


m2 v

R2  | q | B
2

 |q| v B 

m v2
R
R1 m1

R 2 m2
 R
m v
.
|q| B
R1
m
 1
2 R1 m2


m1 1
 .
m2 2
Resposta da questão 3:
Dados: Δx  L; q  e  q  e .
a) A força resultante sobre o elétron é a força elétrica:
Fres  Felet  m a | q | E  m a | e | E 
|e|E
.
m
b) Como a força elétrica atua apenas no eixo y, no eixo x a componente da velocidade
permanece constante, igual a v0. Então:
L
Δx  v 0 Δt  L  v 0 Δt  Δt 
.
v0
c) No eixo y, o movimento é uniformemente variado. Sendo v0y = 0:
a
1
1 e E L 
Δy  a t 2  Δy 


2
2 m  v0 
2
 Δy 
e E L2
.
2 m v02
d) Aplicando a função horária da velocidade no eixo y, com voy = 0:
vy  a t  vy 
eE L

m v0
 vy 
eE L
m v0
.
Resposta da questão 4:
[D]
Dados: v  10 m / s; B  0,5 T; q  10μC  10 –5 C; m  10  10 –20 kg  10 –19 kg; d 
2
r.
2
Analisando a figura:
www.nsaulasparticulares.com.br
Página 11 de 18
 2 r
2 
d 
cos θ  
r
r
Em radianos:
ΔS
π ΔS
θ


r
4
r
 cos θ 
2
2
 ΔS 
π
r.
4
 θ
π
.
4
I
A força magnética age como resultante centrípeta.
Fm  Rcent
 |q | v B 
m v2
r

v
|q| B r
.
m
II
Dividindo (I) por (II), encontramos o tempo para a partícula percorrer o arco ΔS :
Δt 
ΔS π r
m


v
4 |q| B r
 Δt 
π m
ΔS
π  10 19


v
4 | q | B 4  105  0,5

Δt  5 π  1015 s.
Resposta da questão 5:
Sabemos que condutores paralelos percorridos por correntes elétricas de sentidos opostos
repelem-se, devido à interação eletromagnética entre eles, onde a intensidade da força é dada
μ .i .i .L
por: F  0 1 2 , sendo que:
2.π.r
F: intensidade da força trocada entre os condutores;
µ0: permeabilidade magnética do meio. No vácuo µ 0=4.π.10-7 (unidades no S.I.);
i1: intensidade da corrente elétrica que percorre o fio 1;
i2: intensidade da corrente elétrica que percorre o fio 2;
L: comprimento do fio;
r: distância entre os fios.
Considerando a tensão T nos cabos nula, teremos as seguintes forças atuando nos fios:
www.nsaulasparticulares.com.br
Página 12 de 18
Como o fio de cima pesa 0,080 N/m, teremos: P=0,080.L (em Newtons), onde L representa o
comprimento do fio em metros.
μ .i .i .L
μ .i .i
F  P  0 1 2  0,080.L  0 1 2  0,080
2.π.r
2.π.r
Substituindo os valores:
μ0 .i1.i2
4.π.107.20.40
 0,080 
 0,080  r  2x103 m
2.π.r
2.π.r
Resposta da questão 6:
Dados:
R  5; r  5; m  500g  0,5kg; L  50cm  0,5m; i  5A; B  0,4T; k  80N / m; g  10m / s2
a) Aplicando a lei de Ohm-Pouillet para o circuito:
  R  r  i     5  5  5    50 V.
A potência elétrica dissipada é:
2
Pot  R i2  5  5 
 Pot  125 W.
b) Pela Regra da mão direita, concluímos que a força magnética na barra é vertical e para cima
e tem intensidade:
Fmag  BiL sen90º  0,4  5  0,5   1 N.
O peso da barra é:
P  mg  0,5 10   P  5 N.
Como o peso tem intensidade maior que a da força magnética, a mola está distendida, isto
é, a força elástica  Fel  é para cima, conforme indicado no esquema:
Do equilíbrio:
Fel  Fmag  P  80x  1  5  x 
4
 0,05 m  x  5 cm.
80
www.nsaulasparticulares.com.br
Página 13 de 18
Resposta da questão 7:
[E]
Dados: B = 5  10
–4
–19
–14
T; q = 1,6  10 C; F = 1  10 N; θ = 90°.
Da expressão da força magnética:
F | q | v B senθ  v 
F
1,4  1014

q B sen90 1,6  1019  5  104

F  1,25  108 m / s.
Resposta da questão 8:
[A]
A força magnética é a força centrípeta. Portanto:
qvB  m
v2
qBR  q 
v
   BR  v  108 x0,4x10x10 3  4,0x105 m/s.
R
m
m
Resposta da questão 9:
[D]
A força magnética sobre um fio é dada pela expressão: F  i. xB .
A regra da mão direita dá a direção e o sentido da força.
Utilizando a regra da mão direita concluímos a força em cada caso, como mostra a figura
abaixo:
www.nsaulasparticulares.com.br
Página 14 de 18
Resposta da questão 10:
02 + 08 + 16 = 26
Analisemos, então, as proposições:
01) Incorreta: usando a regra da mão direita nº 1, pode-se concluir , pela figura abaixo, que o
v
v
vetor indução magnética no fio 4 aponta para o nordeste, pois a soma B1  B2 tem sentido
v
para o nordeste e B 3 também tem sentido para o nordeste.
02) Correta: usando a regra da mão direita nº 2, conclui-se que a força magnética aponta para
o sudeste.
04) Incorreta: condutores percorridos por corrente de mesmo sentido se atraem.
08) Correta: a intensidade da força magnética trocada entre dois condutores percorridos por
corrente i é:
B
0 i2 L
2 r
, ou seja, é inversamente proporcional à distância entre eles.
Assim, o fio 2 exerce sobre o fio 3 força de maior intensidade que o fio 1 exerce sobre o fio 3.
16) Correta: A figura mostra os vetores indução magnética dois fios 1, 3 e 4 no pontos do plano
onde passa o fio 2. O vetor indução magnética nesse ponto é o resultante dos campos dos
fios 1 e 3 B13 , somado ao do fio 4 B4 , apontando, portanto, para o sudoeste.
 
 
www.nsaulasparticulares.com.br
Página 15 de 18
v
v
32) Incorreta: pela figura, notamos que a soma B1  B3 é nula, sendo então o vetor indução
v
v
magnética no centro do quadrado igual a B2  B4 , apontando para o nordeste.
Resposta da questão 11:
A figura abaixo mostra o campo magnético produzido pela corrente i 1 e a força de atração
que tal campo produz no fio onde circula i 2.
μ0 .i1
.
2 πr
Como a força de atração é dada pela expressão F  BiL , temos:
μ i
F μ 0i1
F  0 1 .i2 .L 

.i2 (01)
2 πr
L 2 πr
O campo produzido por i 1 é dado pela expressão B1 
Pela Lei de Ohm  V  Ri , temos:
1  1.i1  i1  1,0A
1  2i2  i2  0,5A
Voltando à equação 01, temos:
F 4π  107  1 0,5

 106 N / m
L
2π  0,1
Resposta da questão 12:
Dados:  = 48 V; R = 9  ; r = 1  ; B = 2,5 T; Lab = 50 cm = 0,5 m; sen 37º = 0,6.
A resistência equivalente do circuito é:
R
9
Req   2r   2  Req  5 .
3
3
Calculando a corrente total (i):
www.nsaulasparticulares.com.br
Página 16 de 18
i

48

Req
5
 i  9,6 A.
A corrente no trecho ab é:
i 9,6
iab  
 iab  3,2 A.
3
3
Aplicando a expressão da força magnética sobre um condutor:
F  BiabLab sen37º  2,5  3,2  0,5  0,6  
F  2,4 N.
Resposta da questão 13:
[D]
A regra da mão direita esclarece
Resposta da questão 14:
F – F – F – V – F.
A figura ilustra a primeira solução, mostrando as linhas de indução criadas pelas correntes IA e
IC. Logo, sobre o fio B os vetores indução magnética, tanto devido à corrente IA como devido à
corrente IC estão dirigidos para fora do plano da figura, o que acarreta um vetor resultante no
mesmo sentido, para fora do plano da figura.
Aplicando a regra da mão direita nº 2 (regra do “tapa”) encontra-se o sentido da força
magnética, dirigida da direita para a esquerda.
Uma segunda solução pode ser encontrada pensando da seguinte maneira: os fios A e B se
atraem porque as correntes têm o mesmo sentido. Portanto, A exerce uma força sobre B
dirigida para a esquerda. Os fios B e C se repelem porque as correntes IB e IC têm sentidos
opostos. Portanto, a força exercida sobre B pelo fio C também é dirigida para a esquerda. A
resultante, então, está dirigida para a esquerda.
www.nsaulasparticulares.com.br
Página 17 de 18
Resposta da questão 15:
Se a mola sofre distensão, a força magnética tem sentido para a direita. Aplicando a regra da
mão direita, conclui-se que o vetor indução magnética é perpendicular ao plano da página, dela
saindo, como indica a figura.
Fmag
Interbits®
i
Na posição de equilíbrio a forma magnética tem a mesma intensidade da força elástica.
Dados: i  0,5 A; x  1 cm  10–2 m; k  2,5 N / m; L  10 cm  10–1m.
Fmag  Felast

B iLk x

B
k x 2,5  102

 5  10 1 
i L 0,5  101
B  0,5 T.
Resposta da questão 16:
[E]
Resposta da questão 17:
[D]
Para que o campo magnético atue sobre uma carga elétrica, ela deve estar em movimento em
uma direção diferente do campo.
Resposta da questão 18:
[C]
Resposta da questão 19:
[E]
Resposta da questão 20:
[A]
Resposta da questão 21:
[D]
www.nsaulasparticulares.com.br
Página 18 de 18