Existência de Solução
Sist. Lin. II
Sist. Lin. II
Notação:
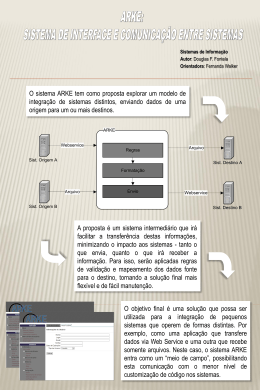
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
Sistemas
Lineares
Sistemas Lineares – 2a Parte
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
Casos Especiais
Paulo Goldfeld
Marco Cabral
Departamento de Matemática Aplicada
Universidade Federal do Rio de Janeiro
0 − zero
1 − um
− não-zero
? − qualquer quantidade
1o caso: sistema totalmente escalonado da forma


? ? ··· ? ?
 .. .. . .
. . 
 . .
. .. .. 


 ? ? ··· ? ? 
0 0 ··· 0 1
0x1 + 0x2 + · · · + 0xn = 1 ⇒ conjunto-solução = { }
sistema inconsistente
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
1 / 28
Álgebra Linear II 2008/2
Exemplos
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
2 / 28
Solução Única
Sist. Lin. II
Sist. Lin. II
Exemplo (sistema inconsistente)
Sistemas
Lineares
Sistemas
Lineares


1 0 0
 0 1 0 
0 0 1
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
2o caso: sistema totalmente escalonado da forma


1 0 ··· 0 ?
 0 1 ··· 0 ? 


 .. .. . .
. . 
 . .
. .. .. 
0 0 ··· 1 ?

x1 = ?



 x2 = ?
..
..

.
.



xn = ?
Exemplo (sistema inconsistente)


1 −3 0 5 0
 0
0 1 2 0 
0
0 0 0 1
⇒ conjunto-solução = {(?, ?, . . . , ?)}
solução única
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
3 / 28
Álgebra Linear II 2008/2
Exemplos
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
Infinitas Soluções
Sist. Lin. II
Sist. Lin. II
Exemplo (sistema com solução única)
Sistemas
Lineares
Produto Matriz-Vetor
Casos Especiais
3o caso: sistema totalmente escalonado
não se enquadra nos casos anteriores
Sistemas
Lineares

1 0 0 −2
 0 1 0
0 
0 0 1 11

Após Escalonamento


1 −3 0 5 0
4
 0
0 1 2 0
0 
0
0 0 0 1 −2
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
Suponha conhecidos os valores de x2 e x4 :
Exemplo (sistema com solução única)

1
 0

 0
0
Álgebra Linear II 2008/2
Prof. Marco Cabral
0
1
0
0
&
0
0
1
0
O sistema pode ser reescrito:

=
4 +3r
 1x1
1x3
=

1x5 = −2

0
7
0 −4 

0 −3 
1 13
Prof. Paulo Goldfeld
DMA / IM / UFRJ
5 / 28
Álgebra Linear II 2008/2
Infinitas Soluções – cont.
Sist. Lin. II

 1x1
1x3
1x5

Após Escalonamento
= 4 + 3r − 5s
=
−2s
=
−2
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
Produto Matriz-Vetor
Casos Especiais
r e s conhecidos; sistema em 3 incógnitas: x1 , x3 e x5 :


1 0 0 4 + 3r − 5s
 0 1 0

−2s
0 0 1
−2
Solução única: (4 + 3r − 5s, −2s, −2)
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
x2 = r
x4 = s
−5s
−2s
DMA / IM / UFRJ
6 / 28
Infinitas Soluções – cont.
Sist. Lin. II
Sistemas
Lineares
4 / 28
DMA / IM / UFRJ
7 / 28
Sistema em x1 , x3 e x5 :
Reintroduzindo
x2 e x4 :

=
4
+3
 x1



x2
=

x3
=


x4
=



x5 = −2

x1
=
4
+3




x2
=
0
+1

x3
=
0
+0


x4
=
0
+0



x5 = −2
+0

x1
=
4
+3




x2
=
0
+1

x3
=
0
+0


Álgebra
x4Marco Cabral= & Prof.0Paulo Goldfeld
+0

 Linear II 2008/2 Prof.

x5 = −2
+0
r
r
−5 s
−2 s
s
r
r
r
r
r
r
r
r
r
r
−5 s
+0 s
−2 s
+1 s
+0 s
−5 s
+0 s
−2 s
DMA / IMs/ UFRJ
+1
+0 s
8 / 28
Infinitas Soluções – cont.
Sist. Lin. II
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
Outro Exemplo com Infinitas Soluções
Sist. Lin. II

− variáveis livres
 x2 , x4
r, s
− parâmetros
Nomenclatura:

x1 , x3 , x5 − variáveis dependentes
Sistemas
Lineares
Casos Especiais
Sistema original: Com eqs. p/ variáveis livres:


x1 =
0
x1 =
1 r






x2 = −7
x2 = −7
−3 s
0
x =
x =
1 s 



 3
 3
x4 =
4
x4 =
4
Número de variáveis livres = n − p, onde
n = (no de incógnitas) = (no de colunas)
p = (no de pivots) = (no de linhas após escalonamento)
?
0 1 0 ?
p
variáveis livres: x1 e x4
0 0 1 ?
?
|
{z
}
n
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
Produto Matriz-Vetor
Casos Especiais
Álgebra Linear II 2008/2
9 / 28
Sist. Lin. II
Sistemas
Lineares
Fazendo r = 0 e s = 0, obtemos a solução
(0, −7, 0, 4) + 0(1, 0, 0, 0) + 0(0, −3, 1, 0) = (0, −7, 0, 4).
Após Escalonamento
Casos Especiais
Infinitas Soluções
Produto Matriz-Vetor
Casos Especiais
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ





1 0 ··· 0 ?
0 1 ··· 0 ? 

.. .. . .
. . 
. .. .. 
. .
0 0 ··· 1 ?
−
−
caso contrário
Álgebra Linear II 2008/2
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
Teorema (Caracterização do Conjunto-Solução)
Se um sistema linear é consistente, o seu conjunto-solução
é um subespaço afim, ou seja, é da forma
xp + xh1 , . . . , xhr .
Prof. Marco Cabral
&
Após Escalonamento

? ? ? ?
 0
? ? ? 
?
0 0 0
Prof. Marco Cabral


1 0 ∗ 0 ∗

0 1 ∗ 0 ∗ 
−→
0 0 0 1 ∗

? ? ? ?
 0
? ? ? 


 0 0
? ? 
?
0 0 0


Álgebra Linear II 2008/2
13 / 28
Prof. Marco Cabral
−→
&
1 0
 0 1

 0 0
0 0
Prof. Paulo Goldfeld
0
0
1
0
0
0
0
1

∗
∗ 

∗ 
∗
DMA / IM / UFRJ
14 / 28
Discussão de Existência e Unicidade
Sist. Lin. II
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
Exemplos:


0 −3 0 −1
6
√
 0
0 0
π
9 
0
0 0
0 311
−→
inconsistente

13
2 0 −6 33
0 10−7 2
9
1 
0
0 0
3
0
−→
infinitas soluções
1 variável livre

2 2
−8 12
0
1 
 0 e3
11 1
2 

 0 0 log(3) 2
0 
0 0
0 77 −3
−→
solução única
solução única

−
caso contrário
Álgebra Linear II 2008/2
12 / 28


0 1 ∗ 0 0
−→  0 0 0 1 0 
0 0 0 0 1


−
DMA / IM / UFRJ
Casos Especiais

··· ? ?
··· ? ? 

. . 
..
. .. .. 
···
?
Prof. Paulo Goldfeld
Produto Matriz-Vetor
infinitas soluções
(n − p) variáveis livres
DMA / IM / UFRJ
&

0
? ? ?
 0 0 0
? 
0 0 0 0
solução única
Prof. Paulo Goldfeld
Prof. Marco Cabral

Sistemas
Lineares

?
 0

 .. ..
 . .
0 0
10 / 28
Sist. Lin. II
A partir da forma escalonada (Parte I do algoritmo):


? ? ··· ? ?
 .. .. . .
.. .. 
 . .
. . .  −
inconsistente


 ? ? ··· ? ? 
0 0 ··· 0

DMA / IM / UFRJ
Relação entre Forma Escalonada e
Forma Totalmente Escalonada
Discussão de Existência e Unicidade
Sist. Lin. II
Prof. Paulo Goldfeld
Um sistema linear pode ter ou não soluções (ser
consistente ou inconsistente).
Álgebra Linear II 2008/2
11 / 28
A partir da forma totalmente escalonada:


? ? ··· ? ?
 .. .. . .
. . 
 . .
. .. ..  −
inconsistente


 ? ? ··· ? ? 
0 0 ··· 0 1

&
Eliminação de Gauss.
Discussão de Existência e Unicidade
Após Escalonamento
Prof. Marco Cabral
Prova
Cada escolha dos parâmetros r e s gera uma solução
distinta e toda solução corresponde a alguma escolha dos
parâmetros.
Sistemas
Lineares
0
−3
1
0
Produto Matriz-Vetor
Fazendo r = 3 e s = −2, obtemos a solução
(0, −7, 0, 4) + 3(1, 0, 0, 0) − 2(0, −3, 1, 0) = (3, −1, −2, 4).
Sist. Lin. II
r
r
r
r
Conjunto-Solução e Subespaço Afim
Conjunto-solução:
{(0, −7, 0, 4) + r (1, 0, 0, 0) + s(0, −3, 1, 0) | r , s ∈ R}
Álgebra Linear II 2008/2
1
0
0
0
Conjunto-solução:
{(0, −7, 0, 4) + r (1, 0, 0, 0) + s(0, −3, 1, 0) | r , s ∈ R}
Gerando Soluções
Após Escalonamento
variáveis livres: x1 = r
x3 = s
Produto Matriz-Vetor
Tomam-se como variáveis livres aquelas associadas a
colunas sem pivots.
Sistemas
Lineares
Após Escalonamento
Variáveis Livres
Casos Especiais
Sist. Lin. II
0 1 3 0 −7
0 0 0 1
4
&
infinitas soluções
(n − p) variáveis livres
Prof. Paulo Goldfeld
DMA / IM / UFRJ
15 / 28
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
16 / 28
s
s
s
s
Produto Matriz-Vetor
Produto Matriz-Vetor: exemplo
Sist. Lin. II
Sistemas
Lineares
Após Escalonamento
Sist. Lin. II
Exemplo
Definição (Produto Matriz-Vetor)


Sistemas
Lineares
Dados a matriz Am×n =  a1 · · · an  e o vetor
Após Escalonamento
Produto Matriz-Vetor
Produto Matriz-Vetor
Casos Especiais
Casos Especiais

x1
n
X
 .. 
xj aj .
x =  . , define-se o produto Ax =
j=1
xn

=
=
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
Sist. Lin. II
Produto Matriz-Vetor (outra interpretação)
A i-ésima entrada do vetor b = Ax é dada pelo produto
escalar da i-ésima linha de A com o vetor b.
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
Produto Matriz-Vetor
Casos Especiais
Casos Especiais
Definição (produto escalar)
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
−1
2
Prof. Paulo Goldfeld
DMA / IM / UFRJ
n
X
a11 a12 · · · a1n
 a21 a22 · · · a2n

 ..
..
..
..
 .
.
.
.
am1 am2 · · · amn
uj vj .
Prof. Paulo Goldfeld
DMA / IM / UFRJ
19 / 28
Álgebra Linear II 2008/2
Prof. Marco Cabral
&





x1
x2
..
.
18 / 28





 
 
=
 
xn
b1
b2
..
.



.

bm
Prof. Paulo Goldfeld
DMA / IM / UFRJ
20 / 28
Propriedades do Produto Matriz-Vetor
Sist. Lin. II
As duas interpretações do produto matriz Ax vetor
correspondem a duas interpretações geométricas do
sistema linear Ax = b.
Ax é linear em x
Sistemas
Lineares
Após Escalonamento
por linhas:
interseção de hiperplanos;
Produto Matriz-Vetor
A(x + y) = Ax + Ay
A(αx) = α(Ax)
Casos Especiais
por colunas:
b como combinação linear das colunas de A.
Corolários
Se Axp = b e Axh = 0, então A(xp + xh ) = b.
Se Ax2 = Ax1 = b, então A(x2 − x1 ) = 0.
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
Álgebra Linear II 2008/2
21 / 28
Sist. Lin. II
Sist. Lin. II
Definição (sistema homogêneo)
Sistemas
Lineares
Sistemas
Lineares
Após Escalonamento
Casos Especiais
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
22 / 28
Sistemas Homogêneos
Sistemas Homogêneos
Produto Matriz-Vetor
Prof. Marco Cabral
Após Escalonamento

a11 x1 +a12 x2 · · · +a1n xn = 0




 a21 x1 +a22 x2 · · · +a2n xn = 0
Ax = 0,
..
..
..
..
..

.

.
.
.
.



am1 x1 +am2 x2 · · · +amn xn = 0
Produto Matriz-Vetor
Lado direito de zeros preservado por oper. fundamentais.




? ··· ? 0
∗ ··· ∗ 0
 .. . . .. .. 
 .. . . .. .. 
 .
. . .  ∼  .
. . . 
? ··· ? 0
Casos Especiais
∗ ··· ∗ 0
Forma escalonada nunca apresenta linha
0 ··· 0
.
Determina-se p (escalonamento):
Definição (solução trivial)
p=n
⇒
solução única (apenas a trivial)
O vetor nulo 0 = (0, 0, . . . , 0) é sempre solução do sistema
homogêneo. Esta solução é chamada solução trivial.
p<n
⇒
infinitas soluções, (n − p) variáveis livres
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
23 / 28
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
+0
(1 × 2) + (2
(4 × 2) + (5
bm


b1
b2
..
.
1
4
(2 × 1) + (0
(2 × 4) + (0
=
&

=
Prof. Marco Cabral
= 2
(2 × 1) + (0 × 2) + (−1 × 3)
(2 × 4) + (0 × 5) + (−1 × 6)

Sistemas Lineares x Produto Matriz-Vetor
Sist. Lin. II
2
3
−1
5
6
a11 a12 · · · a1n
 a21 a22 · · · a2n

O sistema linear  .
..
..
..
 ..
.
.
.
am1 am2 · · · amn
j=1
&
+0

1 2 3
4 5 6
pode ser reescrito como Ax = b, isto é,
hu, vi = u · v =
Prof. Marco Cabral

O produto escalar (ou produto interno) dos vetores u ∈ Rn e
v ∈ Rn é dado por
Álgebra Linear II 2008/2
1
4
Sistemas Lineares x Produto Matriz-Vetor
Sist. Lin. II
Após Escalonamento
Álgebra Linear II 2008/2
17 / 28
Produto Matriz-Vetor
Sistemas
Lineares
= 2
Em palavras, o produto matriz vetor Ax é a combinação
linear das colunas de A, usando por coeficientes as
entradas do vetor x.

2
 0 
−1

1 2 3
4 5 6
24 / 28
Relação entre Sistema Não-Homogêneo e
Sistema Homogêneo Associado
Sist. Lin. II
Sistemas
Lineares
0 1 3 0 −7
0 0 0 1
4

x1



x2

 x3

x4
Após Escalonamento
Produto Matriz-Vetor
Casos Especiais
1 r
=
= −7
=
=
4
Relação entre Sistema Não-Homogêneo e
Sistema Homogêneo Associado

x1



x2
−3 s
1 s 
 x3

x4
=
0
= −7
=
0
=
4
1
0
0
0
r
r
r
r
0 1 3 0 0
0 0 0 1 0

x1



x2
 x3


x4
=
=
=
=
1 r
0

x1



x2
−3 s
1 s 
 x3

x4
0
−3
Sistemas
1
Lineares
0
s
s
s
s
Sistema homogêneo com solução única:




? ··· ? 0
··· ∗ 0
 ? ··· ? 0 
 .. . . .. .. 


 .. . . .. ..  ∼  .
. . . 
 .
. . . 
0
0 ···
? ··· ? 0
Após Escalonamento
Produto Matriz-Vetor
Conjunto-solução:
{(0, −7, 0, 4) + r (1, 0, 0, 0) + s(0, −3, 1, 0) | r , s ∈ R}
Sist. Lin. II
Casos Especiais
=
=
=
=
1
0
0
0
r
r
r
r
0
−3
1
0
Sistema não-homogêneo com mesma matriz:





? ··· ? ?
·
·
·
∗
∗
 ? ··· ? ? 
 ..


 .

. . 
 .. . . .. ..  ∼  .. . . . .. ..  ou  .
 .
 0
. . . 
0 ···
∗
? ··· ? ?
0
s
s
s
s
Conjunto-solução:
{r (1, 0, 0, 0) + s(0, −3, 1, 0) | r , s ∈ R}
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
25 / 28
Álgebra Linear II 2008/2
Relação entre Sistema Não-Homogêneo e
Sistema Homogêneo Associado
Casos Especiais
Prof. Paulo Goldfeld
DMA / IM / UFRJ
26 / 28
Sist. Lin. II
⇒ ⇐
Ax = b
Ax = 0
Sistemas
Lineares
Após Escalonamento
Produto Matriz-Vetor
&




Sistemas com Mesma Matriz de Coeficientes
Sist. Lin. II
Sistemas
Lineares
Prof. Marco Cabral

··· ∗ ∗
. . .. ..
. . .
···
∗
··· 0
Após Escalonamento
sol. = xp + xh1 , . . . , xhr
sol. = xh1 , . . . , xhr
ouou
1 2 4
2 5 9
1 2 3
2 5 7
1 2 4
0 1 1
l1 ← l1 − 2l2
1 0 2
0 1 1
1 2 3
0 1 1
l1 ← l1 − 2l2
1 0 1
0 1 1
l2 ← l2 − 2l1
Produto Matriz-Vetor
Casos Especiais
l2 ← l2 − 2l1
sol. = { }sol. = { }
Se um sistema não-homogêneo é consistente, o subespaço
afim que forma o seu conjunto-solução é uma translação do
subspaço vetorial que forma o conjunto-solução do sistema
homogêneo associado.
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
27 / 28
1 2 4 3
2 5 9 7
∼
1 2 4 3
0 1 1 1
∼
1 0 2 1
0 1 1 1
Evitamos retrabalho aumentando a matriz
com vários lados direitos de uma vez.
Álgebra Linear II 2008/2
Prof. Marco Cabral
&
Prof. Paulo Goldfeld
DMA / IM / UFRJ
28 / 28