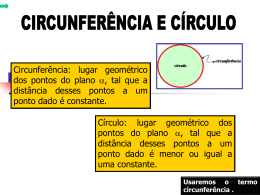
Relações Trigonométricas na
Circunferência
Introdução
Uma das invenções mais importantes da história da humanidade foi a roda, por
volta de 3000 a.C.
Figura 1
Talvez essa ideia tenha surgido da observação de formas arredondadas
existentes na natureza, por exemplo, um tronco de árvore que pode rolar quando
empurrado.
A partir dessa ideia, foi possível chegar à roda e seus vários tipos: rodas de
carroças, de carros, de locomotivas, rolamentos, engrenagens, entre outras.
Nesta apostila daremos ênfase à linha que contorna o círculo, ou seja, à
circunferência.
Relações Métricas na Circunferência
Na Figura 1 tem-se uma circunferência de centro O e raio R.
Figura 2
Se considerarmos a circunferência mais a sua parte interna, temos um círculo
(Figura 3).
26
33 1
Figura 3
Contornando um círculo com um fio e depois o esticando, obtemos o comprimento
C da circunferência. Na figura 4 observa-se essa definição.
𝐶 = 𝜋𝐷
ou 𝐶 = 2𝜋R
𝜋 = 3,1415926
Figura 4
Desse modo, tem-se que C é o comprimento da circunferência, D é o diâmetro e
R o raio. Além disso, é uma constante que equivale a aproximadamente 3,14.
Arcos de Circunferência
Os pontos A e B dividem a circunferência em duas partes. Cada uma dessas
partes é denominada arco da circunferência.
arco AB
O Arco menor é indicado por arco
AB.
Figura 5
Quando nos referimos ao arco maior, marcamos mais uma letra nesse arco.
27
34
1
arco AXB
Figura 6___________
Arcos e Ângulos
Dividindo uma circunferência em 360 partes iguais, cada uma dessas partes é um
arco de 1º (um grau).
Por isso dizemos que a circunferência toda tem 360º.
Esse raciocínio pode ser interpretado melhor na Figura 7.
Figura 7
Nas figuras abaixo se pode observar que a medida em graus de um arco é igual à
medida em graus do ângulo central correspondente.
Como o ângulo destacado na cor laranja mede
90º, o arco destacado na cor vermelha também
mede 90º.
Figura 8
28
35 1
Neste caso o ângulo mede 360º, logo, o arco
destacado na cor vermelha também mede 360º.
Figura 9
A mesma situação ocorre para os casos abaixo:
med(AB)= 30º
Figura 10
med(AXB)= 270º
Figura 11
med(AB)= 90º
Figura 12
Os submúltiplos do grau são o minuto e o segundo. Dessa forma, tem-se:
29
36 1
•
Um minuto é igual a
•
Um segundo é igual a
do grau.
do minuto.
Usando a simbologia:
°
Grau
'
Minuto
''
Segundo
Exemplo: Se a medida de um arco é 50 graus, 15 minutos e 27 segundos, indicase: 50º 15' 27''.
Comprimento de um arco de circunferência
Observando a imagem abaixo, pode-se afirmar que:
O arco AC mede 120º, e o arco AB mede 60º.
O arco AD mede 180º, e o arco AB mede 60º.
Figura 13
Com isso, conclui-se que o comprimento de um arco é diretamente proporcional a
sua medida em graus.
Retas e Circunferência
Analisando a Figura 14, tem-se:
C e F são pontos externos à circunferência.
B e O são pontos internos à circunferência.
A, E e G são pontos da circunferência.
AE é uma corda onde os pontos A e E
pertencem a mesma circunferência.
Figura 14
AG é o diâmetro, pois, a corda passa pelo
centro da circunferência.
Em um plano, uma reta e uma circunferência podem ter em comuns dois pontos
distintos, um único ponto ou nenhum ponto. Observe os casos a seguir:
30
37
1
A reta s e a circunferência têm dois pontos em comum,
A e B distintos. Logo, s é secante à circunferência.
Figura 15
A reta t e a circunferência têm um único ponto E em
comum. Logo, t é tangente à circunferência. O ponto
E é o ponto de tangência.
A reta tangente a uma circunferência é perpendicular
ao raio no ponto de tangência. (Ver aplicativo no
Geogebra)
Figura 16
A reta u e a circunferência não têm nenhum ponto em
comum. Logo, u é externa a circunferência.
Figura 17
Relação entre as Cordas
Consideremos as cordas
Figura 18.
e
que se interceptam no ponto P. Conforme a
Figura 18
Observando os triângulos PAD e PCB, tem-se:
𝐴
𝐶 (medem
𝐵𝐷
:
2
ângulos inscritos no mesmo arco BD)
Além disso, observa-se também que
31
38
1
̂
̂
(são opostos pelo vértice).
Logo,
Como esses triângulos são semelhantes, podemos escrever:
meio pelos extremos tem-se:
=
. Fazendo
=
Em resumo, se duas cordas de uma circunferência se interceptam, então, o
produto das medidas das duas partes de uma delas é igual ao produto das
medidas das duas partes da outra.
Relação entre as Secantes
Consideremos dois segmentos
e
; traçados por um ponto P externo à
circunferência, e suas respectivas partes externas
e
. Conforme a Figura
19.
Figura 19
Observando os triângulos PAD e PCB, tem-se:

A ̂ é o ângulo comum aos dois triângulos

(medem
Logo:
que:
2
: ângulos inscritos no mesmo arco
)
. Como esses triângulos são semelhantes, pode-se afirmar
=
Fazendo meio pelos extremos tem-se:
=
.
Em resumo, se por um ponto externo a uma circunferência traçarmos dois
segmentos secantes, então, o produto da medida de um deles pela medida da
sua parte externa é igual ao produto da medida do outro pela medida da parte
externa deste segmento.
Relação entre Secante e Tangente
Consideremos um segmento secante
, sua parte externa
e um
segmento
tangente a uma circunferência, traçados de um mesmo ponto
externo P.
32
39
1
Figura 20
Observando os triângulos PTA e PTB, tem-se:
̂ (medem
2
:
̂
̂
está inscrito no arco
segmento correspondente ao arco
̂
ângulo comum).
, e
é ângulo de
). Logo,
Como esses triângulos são semelhantes, podemos escrever:
meio pelos extremos, tem-se:
̂
2
=
segundo membro em forma de raiz, tem-se:
=
. Fazendo
, passando o expoente para o
= √
.
Em resumo, se por um ponto externo a uma circunferência traçarmos um
segmento secante e outro tangente a ela, então, a medida do segmento
tangente é média geométrica entre as medidas do segmento secante e da sua
parte externa.
REFERÊNCIA BIBLIOGRÁFICAS
BONJORNO, J. R.; BONJORNO, R. A.; OLIVARES, Ayrton. Matemática:
Fazendo a diferença. São Paulo: FTD, 2006.
33
40
1