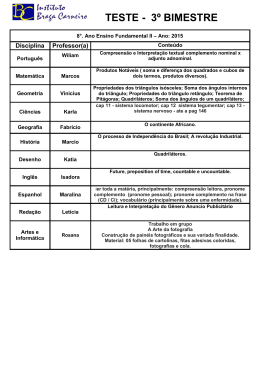
Complemento Schur e aplicações
Cristiane Nespoli
Anderson dos S. Gonzaga∗
Depto. de Matemática e Computação, FCT, UNESP,
19060-900, Pres. Prudente, SP
E-mail: [email protected], [email protected].
RESUMO
Dada uma matriz complexa particionada em blocos da forma
P Q
M=
,
R S
o termo Complemento Schur da matriz S − RP −1 Q, onde P é a matriz não-singular acima, foi
introduzido pela primeira vez em 1968 pela pesquisadora Emilie Haynsworth em [2] e [3]. O
termo foi adotado em honra ao matemático Issai Schur (1875-1941 ) que em 1917 apresentou o
lema (Hilfssatz) no artigo [4]. Pelo mesmo motivo, a fórmula
det(M ) = det(P ) · det(S − RP −1 Q),
(1)
ficou conhecida como fórmula do determinante de Schur. Na verdade, Emilie havia sido orientada
em sua tese de doutorado por Alfred Theodor Brauer (1894-1985), o qual por sua vez, fora
orientado por Schur em 1928.
O complemento de Schur desempenha um papel fundamental em muitas áreas da matemática e engenharia, em geral em problemas que envolvem a solução de sistemas de equações
diferenciais, vide [5] e referências contidas. Na Análise Numérica por exemplo, estes sistemas
aparecem sob a forma de quocientes de determinantes em interpolação polinomial, em frações
continuadas e aproximação de Pade. Em Probabilidade e Estatı́stica, também o complemento
Schur encontra aplicações uma vez que certas inequações matriciais são úteis nestas áreas, dentre as quais, a inequação de Cramer-Rao, que fornece um limite inferior para a covariância
de um estimador não-enviesado, a inequação de Groves-Rothenberg e a inequação multivariada de Cauchy-Schwarz. Além disso, o complemento Schur tem se mostrado uma ferramenta
extremamente útil em Engenharia de Controle.
Neste trabalho apresentamos um resumo envolvendo parte dos estudos em desenvolvimento
junto ao projeto de iniciação cientı́fica de mesmo tı́tulo, vinculado a Bolsa de Apoio Acadêmico
e Extensão (BAAE I) da Unesp. Estes estudos compreendem aspectos teóricos envolvendo o
Complemento Schur e suas propriedades, assim como algumas de suas aplicações. Dentre os
resultados estudados, destacamos aqui a importância deste lema na conversão em inequações
lineares matriciais (LMI) de certas desigualdades matriciais não-lineares e o lema da inversão
de Matrizes.
Uma LMI é uma desigualdade da forma
F (x) := F0 +
m
X
xi Fi > 0
(2)
i=1
onde x = {x1 , x − 2, · · · , xm } ∈ Rm é a variável e {Fi ∈ Rn×n } as matrize simétricas dadas
no problema. Na expressão acima F (x) > 0 significa que F (x) é positiva definida, isto é,
∗
bolsista BAAEI/PROEX Unesp
550
uT F (x)u > 0 para todo u ∈ Rn , u 6= 0. Em outras palavras significa que todos os autovalores
de F (x) são positivos uma vez que autovalores de matrizes simétricas são reais A LMI 2 é uma
restrição convexa em x, isto é, o conjunto {x | F (x) > 0} é convexo.
Aplicando o complemento Schur, dada a LMI
Q(x) S(x)
,
(3)
S(x)T R(x)
onde Q(x), R(x) e S(x) são funções matriciais linearmente independentes em x com R e S
simétricas, isto é, R(x) = R(x)T e S(x) = S(x)T , a expressão (3) fica equivalente a
Q(x) − s(x)R−1 (x)S(x)T > 0, R(x) > 0.
Este resultado (cuja demonstração pode ser encontrada em [5]) é muito utilizado no controle de
sistemas lineares, entre outros, nos quais a solução de LMI se impõem frequentemente.
Por sua vez, lema da inversão de matrizes é também uma aplicação do complemento Schur
com grande apelo à aplicações.
Dada a matriz quadrada
A11 A12
A=
,
A21 A22
onde A11 e A22 também são matrizes quadradas. Supondo que A11 seja não-singular, então A
tem a seguinte decomposição
A11 0
A11 A12
A12
I
A−1
11
=
0 I
A21 A22
A21
A22
Por sua vez, caso A seja não-singular, então sua inversa é dada por
A11 A12
A21 0
A11 − A12 A−1
22
BT ,
=B
A21 A22
0
A22
considerando
B :=
I A12 A−1
22
0
I
>0
Palavras-chave: Complemento Schur, inequações lineares matriciais, inversão de matrizes.
1986)].)
Referências
[1] G. H. Golub and C. F. Van Loan, Matrix Computations, 3ed, The Johns Hopkins University
Press, 1986.
[2] E. V. Haynsworth, On the Schur complement, Basel Mathematical Notes, 20 17 pp., (1968).
[3] E. V. Haynsworth, Determination of the inertia of a partitioned Hermitian matrix. , Linear
Algebra and its Applications, 1 73–81, (1968).
[4] J. Schur, Uber Potenzreihen, die im Innern des Einheitskreises beschrankt sind [I]. Journal
fiir die reine und angewandte Mathematik, 147 (1917), 205-232; reprinted in Brauer and
Rohrbach [71, Band II, pp. 137-164 (1973)] in Fritsche k Kirstein [177, pp. 22-49 (1991)].
(Translated into English in Schur [409, pp. 31-59 (1986)]).
[5] F. Zhang, The Schur Complement and Its Applications, Series: Numerical Methods and
Algorithms, Springer, Vol. 4, 1995.
551